2.4 The Copernican Revolution & the “Horror Vacui”
Or How Aristotelian Methods Overthrew Aristotelian Beliefs
A brilliant doctor of canon law, Nicolaus Copernicus (1473–1543) was a man of many talents. As an economist, he studied and reported how uncut or pure gold coins were driven out of circulation by clipped or debased coinage, a principle later rediscovered by Thomas Gresham (1519–1579) and dubbed “Gresham’s Law.” Copernicus was an accomplished mathematician and served as a diplomat and counselor to princes of both the church and state. His other passion was astronomy. His precise observations identified that the path the Earth and Sun take with respect to each other is not exactly a circle, leading him to speculate which orbited around the other.
Since at least 1514, Copernicus had circulated pamphlets among friends and colleagues describing his hypothesis that the Earth travelled around the sun. On his deathbed in 1543, Copernicus is said to have finally viewed the proofs of his magnum opus: De revolutionibus orbium coelestium (On the Revolutions of the Heavenly Spheres). Figure 2.13 compares the geocentric model of Claudius Ptolemy (~100–~170) with the heliocentric model of Nicolaus Copernicus.
The comparison between models was not as simple as it may appear. Both the Ptolemaic and Copernican models required the addition of extra epicycles to agree with observations of planetary motion. To match the observations, the deferents had to be offset from each other by arbitrary amounts. Both models were mathematical messes. Finally, any model that purported the Earth to be in motion defied significant evidence to the contrary.
If the Earth is moving rapidly, why are we not swept off its surface by the resulting strong winds? There is no perceptible “parallax” or relative motion of nearer stars with respect to those believed to be more distant. There is also no easily detectible “Coriolis force” curving the motion of projectiles or falling bodies as might be expected if the Earth were rotating. We now know that this lack of confirmation was due to insufficient precision of measurement, but at the time, observations like these were strong evidence against geo-mobility [[i]].

It is said that “extraordinary claims require extraordinary evidence,” a principle annunciated by Pierre-Simon de Laplace (1749–1827) [[vi]] and more recently popularized by Carl Sagan (1934–1996) [[vii]]. Yet, too often we regard the models with which we are familiar as ordinary while an equivalent but unfamiliar model appears extraordinary. Do we enshrine the status quo and refuse to change our models without extraordinary evidence? This irrationally favors the earlier theory, instead of the best theory.
In fact, Copernicus was not the first to present the heliocentric hypothesis. Nearly two thousand years before Copernicus, Aristarchus of Samos (~310–~230 BC) correctly calculated that the sun was much larger than the Earth and correctly concluded that the Earth went around the sun. Does that mean instead that the geocentric theory should have required extraordinary proof to displace the heliocentric theory? Or vice versa?
When two competing theories correctly explain a common set of data, they may be freely used, one or the other, whichever most easily delivers the correct result. Meanwhile, we seek additional evidence that may allow us to distinguish one model from the other and determine which more correctly describes the underlying reality. Even after we have established that one model is correct, we may continue using a model known to be incorrect in a broader context if it delivers the correct answers more easily for a specific problem.
For instance, even today celestial mechanics calculations often use the geocentric model to make their Earth orbital navigational calculations easier. The Apollo astronauts implicitly used the geocentric model to navigate to the moon and back, and the selenocentric (moon-centered) model to calculate their lunar landing trajectory. When two models compete, the correct standard of proof to choose between them is the preponderance of evidence.
In any event, Copernicus’ model provided the basis for Johannes Kepler (1571–1630) to analyze the meticulous astronomical observations of Tycho Brahe (1546–1601) and derive his Laws of Planetary Motion. Kepler was fascinated with Platonic solids, as we saw in Figure 2.3.

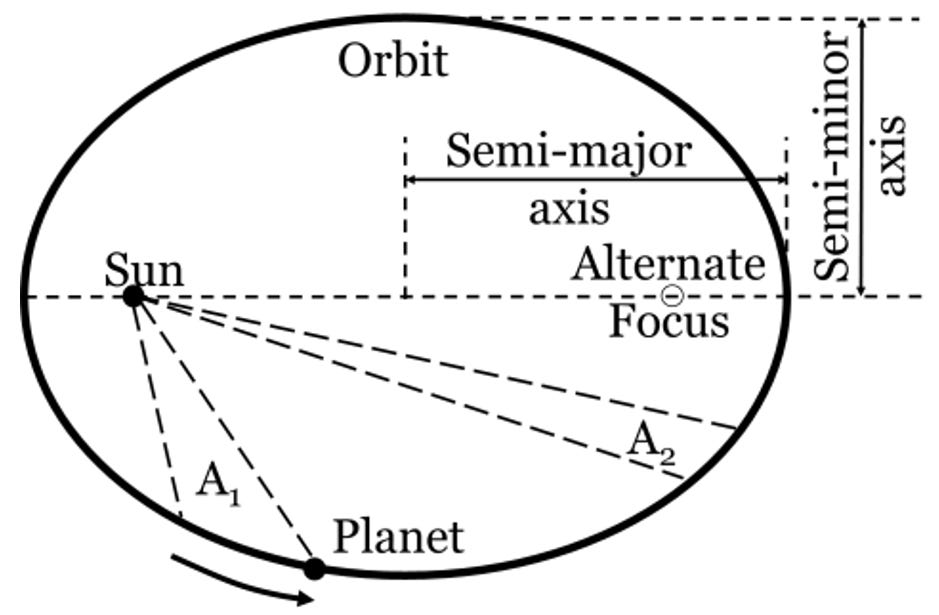
Kepler’s hypothesis was that planetary motion could be explained using a system of nested Platonic solids, a portion of which may be seen in Figure 2.14. His model did reproduce certain numerical relationships or harmonies in the data. But when the utility of his model, proved limited, Kepler forged on, discovering that planetary motion traced out elliptical orbits with the sun at one focus of the ellipse as shown in Figure 2.15. In addition, planets move faster when they are closer to the sun, traversing equal areas in equal time. Finally, he noted a curious “coincidence,” that the period of the orbit was proportional to the cube of the semi-major axis of the ellipse.
To summarize, Kepler’s laws of planetary motion are:
The orbit of a planet is an ellipse with the Sun at one of the two foci.
A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
Writing to Kepler in 1596, Galileo declared:
I esteem myself happy to have as great an ally as you in my search for truth. I will read your work … all the more willingly because I have for many years been a partisan of the Copernican view because it reveals to me the causes of many natural phenomena that are entirely incomprehensible in the light of the generally accepted hypothesis. To refute the latter I have collected many proofs, but I do not publish them, because I am deterred by the fate of our teacher Copernicus who, although he had won immortal fame with a few, was ridiculed and condemned by countless people (for very great is the number of the stupid) [[xii]].
New insights began to arise in our understanding of terrestrial motion as well. Ballistic theory–the science of projectile motion–came into its own with medieval siege warfare, yet the theory had long remained grounded in Aristotelian physics. Terrestrial motion was thought to be linear, celestial motion, circular. Near the Earth, a projectile was thought to follow a straight-line path. As the projectile ascended to the heavens, it adopted a circular path. Curving down and approaching the Earth, the projectile followed a linear path again. Figure 2.16 shows a 1582 woodcut of the “Three-Part” model of a projectile trajectory.

A careful observer, like Leonardo da Vinci (1452–1519), could see the imperfections in this model, but a rigorous mathematical analysis proved difficult. Figure 2.17 shows a 1493 sketch from one of Leonardo’s notebooks.


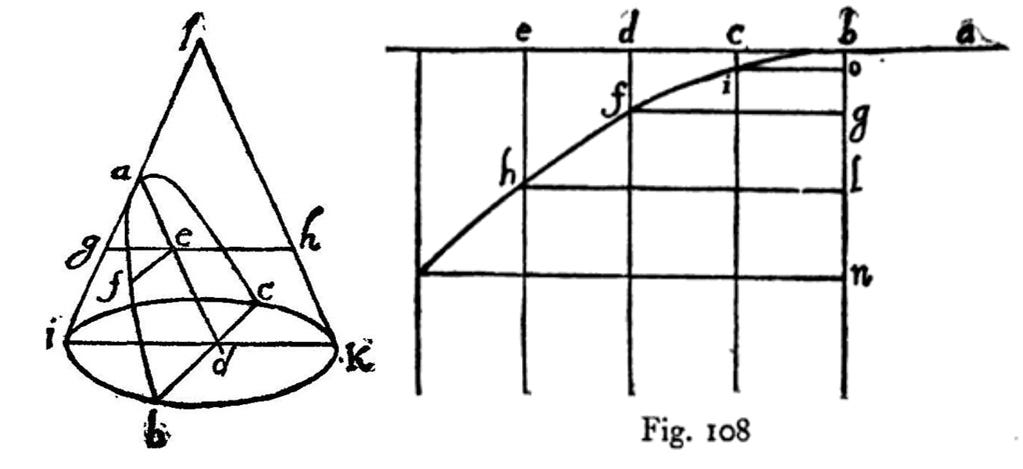
In his 1638 work, Dialogues Concerning Two New Sciences, Galileo reviewed both physics and mechanics [[xvi]]. Topics included the strength of materials, lever arms, pressure, and motion. Compiling previous results and his own meticulous measurements, he described the science of motion and acceleration. Appealing to the writings of Apollonius of Tyana (~AD 15–100), Galileo explained how a parabola arises from a section of a cone, as shown in Figure 2.19. Finally, Galileo describes the uniform motion of a body from a to b on a plane, and then shows how the motion remains uniform in the horizontal direction while accelerating downward in the vertical direction, yielding a parabolic trajectory as also shown in Figure 2.19.
Galileo further argued that the reason a pump can “suck” up water is not because “nature abhors a vacuum,” but because atmospheric pressure can support a column of about 34 feet of water [[xx]]. Galileo’s student, Evangelista Torricelli (1608–1647), used a denser liquid, mercury, to demonstrate the same effect in a smaller scale, showing atmospheric pressure could support about a 30-inch column of mercury – thus inventing the barometer [[xxi]]. Torricelli postulated that we live in a sea of air, and thus the atmospheric pressure and height of the column of mercury it would support would vary with altitude. He validated his prediction with measurements of pressure versus altitude. Figure 2.20 shows Torricelli’s 1643 experimentation with a barometer in the Alps.

In 1648, the brilliant young mathematician, Blaise Pascal (1623–1662), repeated Torricelli’s experiment and extended upon his results. He concluded, “…nature can, and does, tolerate any amount of space empty of any of the substances that we are acquainted with, and that are perceptible to our senses.” Pascal also declared:
Let all the disciples of Aristotle collect the profoundest writings of their master and of his commentators in order to account for these things by abhorrence of a vacuum if they can. If they cannot, let them learn that experiment is the true master that one must follow in Physics; that the experiment made on mountains has overthrown the universal belief in nature’s abhorrence of a vacuum, and given the world the knowledge, never more to be lost, that nature has no abhorrence of a vacuum, nor does anything to avoid it; and that the weight of the mass of air is the true cause of all the effects hitherto ascribed to that imaginary cause [[xxiv]].

By 1657, Otto von Guericke (1602–1686) perfected a vacuum pump that evacuated two 20-inch diameter hemispheres. In spectacular demonstrations, he showed that two teams of eight horses were unable to pull them apart, as shown in Figure 2.22, but they fell apart easily when air was allowed back into the evacuated hemispheres.

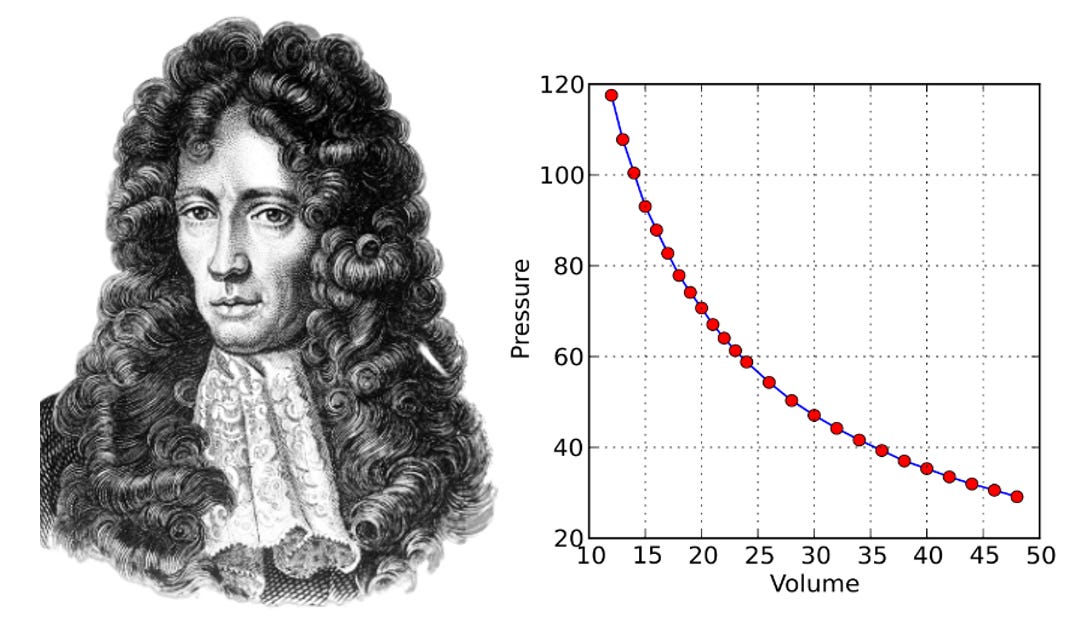
In 1658, Robert Hooke (1635–1703), the able lab assistant of Robert Boyle (1627–1691), completed an easy-to-use air pump that allowed a wide variety of experiments to be performed [[xxviii]]. In 1662, Boyle established that the product of pressure (p) and volume (v) was a constant (pv = k) at a constant temperature, a relation now known as Boyle’s Law. Figure 2.23 shows Robert Boyle and the data by which he established his law [[xxix]]. Boyle would go on to be one of the dozen original founders of the Royal Society in 1660 [[xxx]].
No known or perceptible matter existed within these seventeenth-century vacuums. Birds and mice quickly died in evacuated space. No sound would propagate through them. This seemed to suggest they were truly empty, and yet light and magnetism traversed their emptiness with no difficulty.
By their intimate association with the facts of nature, by holding the observed facts as “ultimate and controlling” [[xxxi]], scientists like Brahe, Kepler, Galileo, Torricelli, Pascal, von Guericke, Boyle, and others were able to identify basic, important physical laws. Their discoveries were firmly rooted in the real world. They were not always consistent, but we can safely classify their work as Aristotelian, even as they made the discoveries that overthrew Aristotle’s own conclusions.
While these Aristotelian discoveries were advancing physical understanding, there were parallel efforts to approach nature from an a priori, deductive, Platonic approach. Next time, we will examine the life and work of René Descartes (1596–1650).
Follow Online:
You may follow me online in other places as well:
Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞
Gab: @aetherczar
Twitter: @aetherczar
Amazon: Hans G. Schantz
[i] Flynn, Michael, “The great Ptolemaic smackdown and down-and-dirty mud-wrassle,” Analog, vol. 133 (no. 1 & 2, January – February, 2013, pp. 14-27. See: https://tofspot.blogspot.com/2013/10/the-great-ptolemaic-smackdown-table-of.html
[ii] Portrait of Ptolemy with an armillary sphere model by Justus van Gent (fl. 1460–1480) and Pedro Berruguete (1450–1504). See: https://commons.wikimedia.org/wiki/File:Ptolemy_1476_with_armillary_sphere_model.jpg
[iii] See: https://gl.wikipedia.org/wiki/Ficheiro:Cassini_apparent.jpg
[iv] Portrait of Copernicus from the Town Hall in Toruń, 1580. See: https://infogalactic.com/info/File:Nikolaus_Kopernikus.jpg.
[v] See: https://commons.wikimedia.org/wiki/File:Copernican_heliocentrism_theory_diagram.svg
[vi] Laplace, Pierre-Simon de, Essai philosophique sur les Probabilités, 5th ed., (Paris: Bachelier, Successeur de Mme Ve Courcier, 1825), pp. 134–135.
[vii] Sagan, Carl, “Encyclopaedia Galactica,” Cosmos, December 14, 1980, Episode 12. 01:24 minutes in. PBS.
[viii] Portrait of Brahe by Eduard Ender (1822-1883). See: https://infogalactic.com/info/File:Tycho_Brahe.JPG
[ix] Tycho Brahe in his lab. Source: Nordisk familjebok (1904), vol.2, p.287-288. See: https://da.wikipedia.org/wiki/Tycho_Brahe#/media/Fil:Tycho_Brahes_stora_murkvadrant,_Nordisk_Familjebok.jpg
[x] See: https://infogalactic.com/w/images/7/74/JKepler.jpg.
[xi] https://en.wikipedia.org/wiki/Mysterium_Cosmographicum#/media/File:Kepler-solar-system-2.png
[xii] Galileo Galilei, Letter to Kepler (1596), as quoted in The Story of Civilization : The Age of Reason Begins, 1558-1648 (1935) by Will Durant, p. 603
[xiii] Ryff, Walther Hermann, Bawkunst Oder Architectur aller fürnemsten/ Nothwendigsten/ angehœrigen Mathematischen vnd Mechanischen Kuensten. Basel 1582, p. ccxv. See: https://en.wikipedia.org/wiki/Theory_of_impetus#/media/File:Buridan-impetus.jpg
[xiv] http://en.wikipedia.org/wiki/User%3APortolanero See also: https://portolanero.neocities.org/Leonardo_Ballistic_Trajectory.png
[xv] See: Galileo Galilei.. Credit: Wellcome Collection. CC BY
[xvi] Galileo, Dialogues Concerning Two New Sciences, New York: The Macmillan Company, 1914, p. 249.
[xvii] Galileo, Dialogues Concerning Two New Sciences, New York: The Macmillan Company, 1914, p. 246.
[xviii] Galileo, Dialogues Concerning Two New Sciences, New York: The Macmillan Company, 1914, p. 249.
[xix] The discovery of the barometer: Torricelli experimenting in the Alps, 1643. Oil painting by Ernest Board. Credit: Wellcome Collection. CC BY
[xx] Maxwell, James Clerk, “Instruments Connected with Fluids,” in Scientific Papers, vol. 2 p. 523-524. .
[xxi] Maxwell, James Clerk, “Instruments Connected with Fluids,” in Scientific Papers, vol. 2 p. 523-524. .
[xxii] See: https://commons.wikimedia.org/wiki/File:Evangelista_Torricelli._Line_engraving_by_A._Hercolani._Wellcome_V0005862EL.jpg
[xxiii] Credit: Blaise Pascal. Lithograph after G. Edelinck after F. Quesnel, junior. Wellcome Collection. Public Domain Mark
[xxiv] Hall, A. Rupert, From Galileo to Newton, New York: Dover, 1981, pp. 252-3.
[xxv] Gaspar Schott (1608 - 1666) - http://www.sil.si.edu/digitalcollections/hst/scientific-identity/fullsize/SIL14-G004-07a.jpg.
[xxvi] Portrait of The Honourable Robert Boyle (1627 - 1691), Irish natural philosopher. Credit: Wellcome Collection. CC BY
[xxvii] https://commons.wikimedia.org/wiki/File:Boyles_Law.svg
[xxviii] Maxwell, James Clerk, “Instruments Connected with Fluids,” in Scientific Papers, vol. 2 p. 523-524. .
[xxix] Boyle, Robert, A Defence of the Doctrine Touching the Spring and Weight of the Air, Propos’d by Mr. R. Boyle in his New Physico-Mechanical Experiments, Against the Objections of Franciscus Linus Wherewith the Objector’s Funicular Hypothesis is also examined, London: Printed by F.G. for Thomas Robinson Bookseller in Oxon: 1662. p. 60. See: https://bvpb.mcu.es/en/catalogo_imagenes/grupo.do?path=11143411 Note that pressure is in inches of mercury and volume is in arbitrary units.
[xxx] Lomas, Robert, Freemasonry and the Birth of Modern Science, New York: Barnes & Nobel Books, 2002, pp. 32-33, 53-54. See: https://amzn.to/46XHRbv.
[xxxi] John Herman Randall, Jr., Aristotle, (New York: Columbia University Press, 1960), p.42.




Excellent presentation, sir! I really look forward to your book.
I wonder if there were no theological reasons to bash on Aristotle back in those days (or even rather petty ones, like upending/deconstructing an erstwhile hero of scholarship). The idea that nature abhors a vacuum is something which easily survives the air pressure experiments -- vacuum has nothing to resist matter intruding upon it, and in this formulation it is fairly consistent with our current understanding of physics.