We’ve accounted for three missing equations in Ohm’s Law. The other four “missing” Maxwell’s equations are the relations for the continuity of charge and the “electric elasticity.” The continuity of charge is a mathematical recognition that if the amount of charge increases or decreases somewhere, then there must be a corresponding current bringing or taking away, respectively, the appropriate amount of charge. Electric elasticity is the relation between the vector electric field (E) and the vector displacement (D). In modern notation, the two are related by the electric permittivity, ε, as follows: D = ε E. More about this “permittivity” which keeps popping up in our equations in a moment.
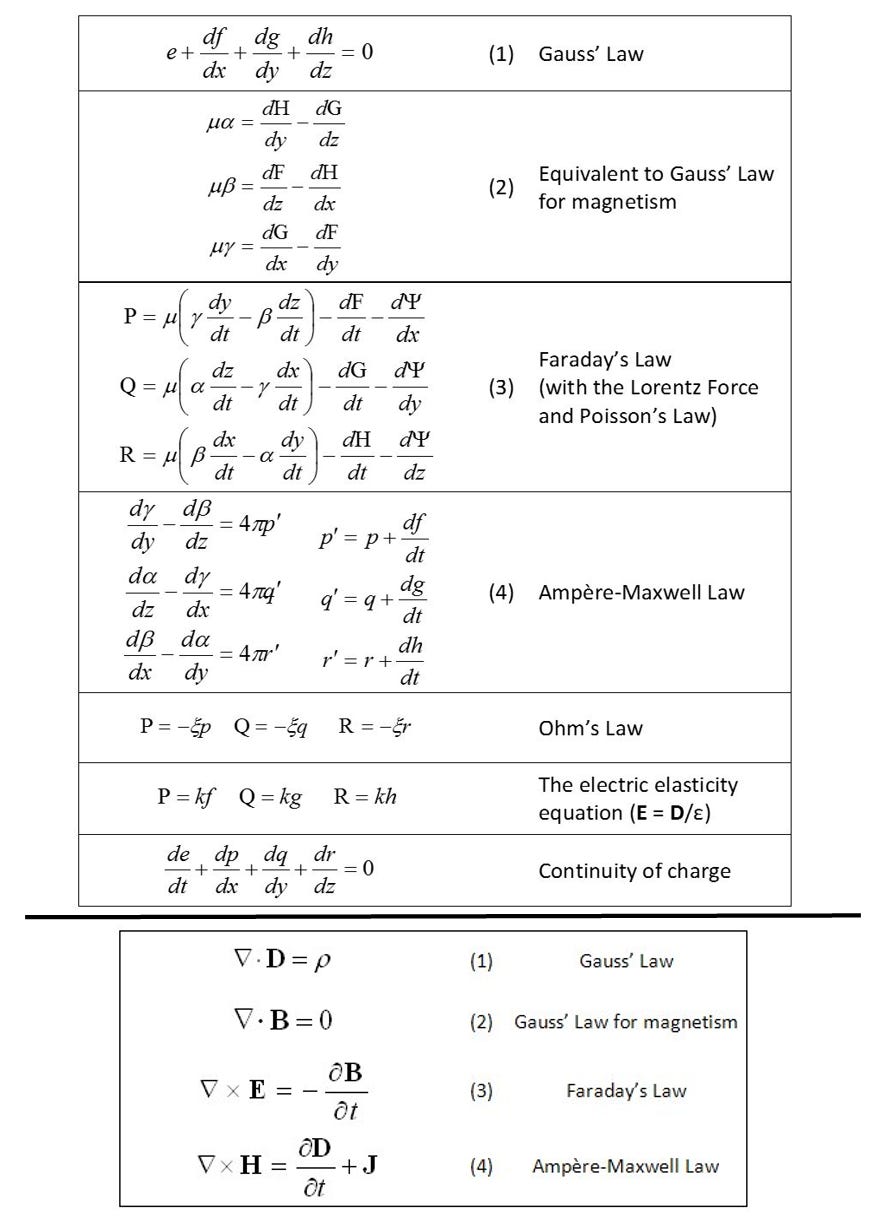
Figure 3.19 compares Maxwell’s own version of his famous equations (top) to Oliver Heaviside’s streamlined four-equation version (bottom). The mathematical details involved in applying these complicated equations are best left to a formal course in electromagnetism. You don’t need to be proficient in vector calculus, however, to appreciate the difference in complexity and the simplification Heaviside’s vector formulation wrought.
For instance, Maxwell wrote the three Cartesian components of the electric displacement as {f, g, h}, and the charge density as “e,” instead of “ρ.” A modern scientist or engineer, using vector notation, would write it as D, instead, and combine the x, y, and z derivatives in the “gradient,” or “nabla” sign (∇).
In addition, Maxwell intermingled potential and field relationships in a way that is confusing to more modern sensibilities. The technical details of the various ways Maxwell derived his equations are in a paper by Alfred M. Bork (1896–1975) [[i]], and the Engineering and Technology History Wiki offers an excellent overview [[ii]].
The following sections consider the four “Maxwell’s equations:” Gauss’s Laws for electricity and magnetism, Faraday’s Law, and Ampère’s Law in further detail. Maxwell may not have worked out each equation all by himself, but he took the individual pieces and fit them together in a way that fully explains and describes electromagnetism.
Next time: 3.4.3 Gauss’s Laws: The Famed Geophysicist Was Also Reputed to be an Excellent Mathematician
Follow Online:
You may follow me online in other places as well:
Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞
Gab: @aetherczar
Twitter: @aetherczar
Amazon: Hans G. Schantz
References
[[i]] Bork, Alfred M., “Maxwell and the Electromagnetic Wave Equation,” American Journal of Physics, vol. 35, no. 9, pp. 844-849. doi:10.1119/1.1974263
[[ii]] See: https://ethw.org/Maxwell%27s_Equations
[[iii]] See: https://ethw.org/File:Maxwell_image_05.jpg.
[[iv]] See: https://ethw.org/File:Maxwell_image_02.jpg.




Seems like a massive "Doh!" moment for Maxwell. Did he live to see how elegantly his equations could be rendered? I bet he would have loved it after chuckling at himself for a bit, of course.
Would Heaviside have done it without Maxwell first?