The great German mathematician, Johann Carl Friedrich Gauss (1777–1855), was born to an illiterate mother who could only recall that his birth was on a Wednesday, eight days before the Feast of the Ascension, forty days after Easter. Easter falls on the first Sunday following the first full moon following the first day of spring, and thus requires accounting for the solar year, lunar phase, and rotation of the Earth. In 1799, Gauss derived a formula to calculate the date of Easter for any year, and he determined the date of his birth to be April 30, 1777 [[i]].
Gauss showed remarkable mathematical talent from a young age. In second grade, it is said his teacher assigned his class the arduous job of adding up all the numbers from one to a hundred. Gauss realized 1+100 = 101, 2+99 = 101, 3+98 = 101, etc. There are fifty such pairs from one to a hundred. He immediately wrote the answer, 5,050, on his slate and presented the solution to his incredulous teacher [[ii]].
No short description can do justice to Gauss’s ground-breaking work in mathematics, let alone his contributions to physics. Gauss pioneered differential geometry, and worked not only in optics, but also in electricity and magnetism. He teamed with Wilhelm Weber (1804–1891) in 1831 to understand geomagnetism and in so doing, derived the law that bears his name [[iii]].

We’ve already seen how electric field lines originate on positive electric charges and end on negative charges, as in the “dipole” or equal and opposite positive and negative charges of Figure 3.18. There is no magnetic charge to serve as a source or sink of a magnetic field line, so magnetic field lines always form closed loops. An interesting wrinkle becomes apparent in studying Gauss’ Law. In the absence of electric charges, for instance in electromagnetic waves, electric field lines also form closed loops, as in Figure 3.21.
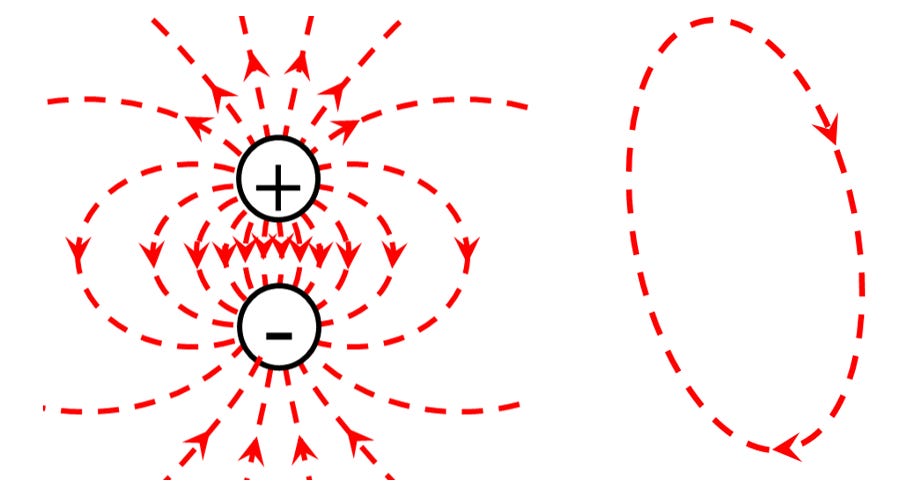
An electric field line shows the direction of the electric force that would act upon a small test charge – a charge too small to perturb the overall field configuration. A magnetic field line shows the orientation of the torque exerted on a small magnet. Thus, iron filings align themselves along magnetic field lines in the manner which originally inspired Faraday to suppose their existence. As Heaviside noted:
Electric and magnetic force. May they live forever, and never be forgot, if only to remind us that the science of electromagnetics, in spite of the abstract nature of the theory, involving quantities whose nature is entirely unknown at present, is really and truly founded upon the observation of real Newtonian forces, electric and magnetic respectively [[vi]].
Gauss’s Law is a mathematical relationship between fields and sources. Figure 3.22 shows the dipole of Figure 3.21 with the addition of closed surfaces A, B, and C seen in cross-section in the plane of the dipole. Imagine them rotated along the axis of the dipole to form surfaces bounding a volume inside. Surface A encompasses no charge, so it has the same number of field lines coming into the surface as going out. In other words, there is no net flux. Surface B encompasses a positive charge and has a variety of field lines emerging from the surface. The number of field lines, or equivalently, the “electric flux,” is proportional to the amount of enclosed charge. Surface C encompasses no net charge, so for every field line passing into C, there is a field line passing out of C. For simplicity, A, B, and C are shown in a plane, but they must be imagined as the cross-sections of surfaces bounding a volume, not boundaries of an area.
Gauss’s Law was not merely a triumph of theoretical physics, but arose from a very practical question: what does the Earth’s magnetic field do? Before Gauss’s discoveries, investigators could determine the direction of the field, but not the intensity. Gauss and Weber devised a procedure involving a torsion balance to calibrate the measuring instrument. They made meticulous measurements of the Earth’s magnetic field in an iron-free measuring hut built to their specifications and gathered similar data from around the world. Figure 3.23 compares Gauss’s result to a modern map of geomagnetic field intensity.
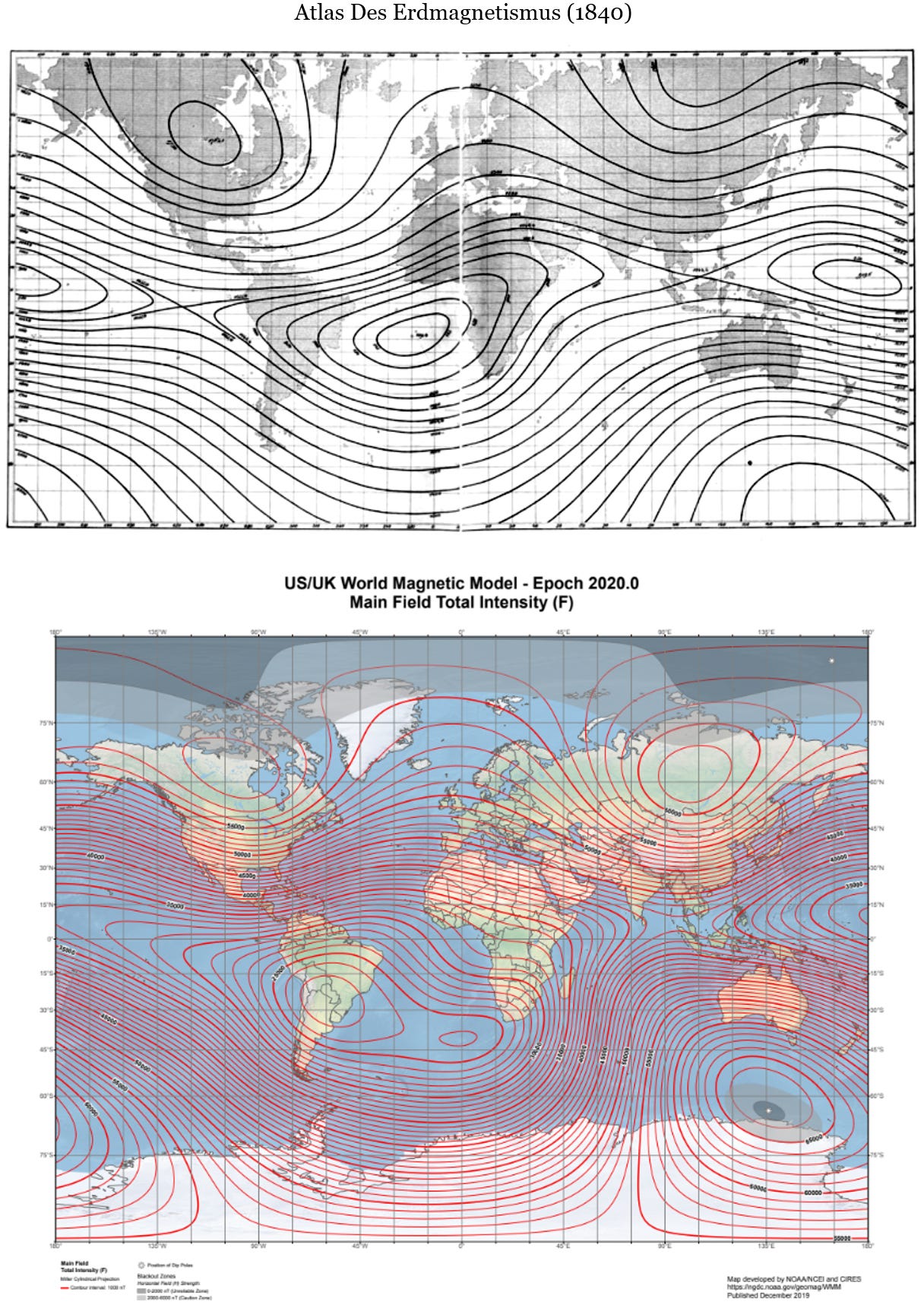
Gauss compiled measurements from around the globe and fit the data using spherical harmonics to interpolate between measurement locations. Gauss’ result was more accurate than a superficial comparison of Figure 3.23 might suggest, because the Earth’s magnetic field has changed modestly since 1840.
The relations we now know as Gauss’s Law have a complicated history. Laplace first derived the equivalent relation for potentials in free space in 1785 in the context of gravitation, and Poisson presented the correct version in the presence of sources in 1813 [[ix]]. Gauss’s Law of Magnetism was a byproduct of Gauss’s efforts to establish that the geomagnetic field at Earth’s surface could be accounted for by magnetic sources distributed within the Earth [[x]]. The full mathematical development of Gauss’s law required an understanding of what came to be known as the divergence theorem. Maxwell credited the Russian mathematician Michael V. Ostrogradskii (1801–1861), but Maxwell’s own proof followed from methods pioneered by Gauss in 1813. Sometimes George Green is credited, but the priority remains unclear [[xi]]. In any event, in recognition of Gauss’s many contributions to magnetic science, the “Gauss” is the cgs (centimeters, grams, and seconds as base units) unit of magnetic flux density.
Like Faraday, Gauss was deeply troubled by instantaneous action at a distance. In an 1845 letter, Gauss proposed to rewrite the equations of electricity in such a way as to allow electric force to propagate with a finite velocity [[xii]]. Gauss’s student, Bernhard Riemann (1826–1866) presented a partial solution to the Göttingen Academy in 1858, but dissatisfied, afterward withdrew it [[xiii]]. The work appeared posthumously in 1867 and anticipated what would now be called “retarded potentials.”
To summarize the most fundamental implications of Gauss’s Law, bound electric field lines begin on positive charges and end on negative charges. Unbound electric field lines form closed loops – this is how electric fields can decouple from charges and propagate elsewhere in an electromagnetic wave. Magnetic fields are always closed loops, whether bound to a current or freely propagating in an electromagnetic wave. Gauss’s Laws – one each for electricity and magnetism – are two of Maxwell’s equations.
Next time, 3.4.4 Ampère’s Law: Two Different Right-Hand Rules - For Currents & Radiation
Follow Online:
You may follow me online in other places as well:
Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞
Gab: @aetherczar
Twitter: @aetherczar
Amazon: Hans G. Schantz
References
[[i]] Director, Bruce, “Mind Over Mathematics, How Gauss Determined the Date of His Birth,” The American Almanac, April 7, 1997. See: http://american_almanac.tripod.com/gauss.htm
[[ii]] Boyer, Carl B., and revised by Uta C. Merzbach, A History of Mathematics, 2nd edition, New York: John Wiley & Sons, Inc., 1991, p. 497.
[[iii]] Ian Stewart, “Gauss,” Scientific American, July 1977.
[iv] By Christian Albrecht Jensen - http://archiv.bbaw.de/archiv/archivbestaende/abteilung-sammlungen/gesamtbestand-des-kunstbesitzes/gelehrtengemaelde/gelehrtengemalde-seiten/ZIMM-0001.html, Public Domain, https://commons.wikimedia.org/w/index.php?curid=6886354
[v] See: https://upload.wikimedia.org/wikipedia/commons/5/55/Wilhelm_Eduard_Weber_II.jpg
[[vi]] Heaviside, Oliver, Electromagnetic Theory, Vol. 3, London: “The Electrician” Printing and Publishing Company, Limited, 1912, p. 1.
[vii] Gauss, Carl Friedrich and Wilhelm Weber, Atlas des Erdmagnetismus, Leipzig: Weidmann’sche Buchhandlug, 1840, 19 Taf XVII Karte für die isodynamischen Linien nach Mercator's Projection.
[viii].Map of intensity of magnetic Earth field in 2015. NOAA/NGDC December 2014. See: https://www.ngdc.noaa.gov/geomag/WMM/image.shtml or https://en.wikipedia.org/wiki/File:World_Magnetic_Field_2015.pdf
[[ix]] Whittaker, Edmund, History of the Theories of Æther and Electricity, vol. 1, New York: Thomas Nelson & Sons, 1951, p. 61.
[[x]] Garland, G.D., “The Contributions of Carl Friedrich Gauss to Geomagnetism,” Historia Mathematica 6 (1979), 5-29. This paper was presented on June 4, 1977, at the Gauss Symposium organized by the Royal Society of Canada at the Ontario Science Centre in Toronto.
[[xi]] Stolze, Charles H., “A History of the Divergence Theorem,” Historia Mathematica, 1978, pp. 437-442.
[xii] James Clerk Maxwell, A Treatise on Electricity and Magnetism, London: Oxford University Press, vol. II, 3rd ed., 1892, pp. 489-490.
[[xiii]] Whittaker, Edmund, History of the Theories of Æther and Electricity, vol. 1, New York: Thomas Nelson & Sons, 1951, p. 240.






We see that Gauss is first and foremost human, using his mathematical talents to correctly deduce his birthdate.
I would of loved to the look on his teachers face when he correctly deduced the 5050 answer to the math problem.
It was Alexander von Humboldt who convinced Gauss to conduct research in magnetism. Here is a quotation from Gauss, in his Intensitas vis magneticae terrestris ad mensuram absolutam revocata, Chapter 5 of Wilhelm Weber’s Main Works on Electrodynamics Translated into English,
Volume I: Gauss and Weber’s Absolute System of Units, edited by André Koch Torres Assis (Montreal: Apeiron, 2021):
For the first light thrown upon this subject we are indebted to the Baron Humboldt, whose attention was particularly directed to it during all his travels, and who has furnished a considerable series of observations, from which the gradual increase of this intensity, from the magnetic equator of the earth towards the magnetic poles, has been deduced. Many observers have since followed the footsteps of that great naturalist; and almost every part of the world to which, in recent times, travellers have penetrated, has furnished its quota of materials, from which already Hansteen (to whom this branch of philosophical inquiry is under great obligation) has been enabled to attempt the construction of an iso-dynamical chart.