3.4.4 Ampère’s Law

Two Different Right-Hand Rules - For Currents & Radiation

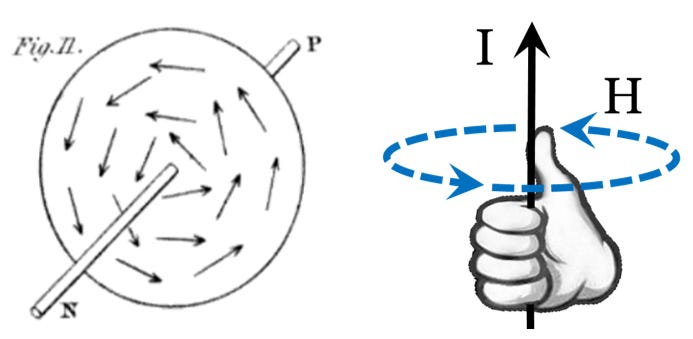
The preliminary investigations of Hans Christian Örsted (1777-1851) established that “magnetism is produced whenever concentrated electricity is passed through space” [[ii]]. He established the circular orientation of magnetic effects around a current, as shown in the vintage illustration of Figure 3.24, by discharging a battery along a conductor, thus magnetizing small needles placed on a plane perpendicular to the wire. The needles then oriented themselves in the circular pattern shown in the figure. The geometry of the magnetic field with respect to a current follows the “right-hand rule:” align the thumb of your right hand with the direction of the current (I), and the magnetic field (H) forms loops in the direction of the fingers of your right hand as in Figure 3.24.

Figure 3.24: 1821 sketch of magnetic effects [[i]], left. Magnetic fields loop around currents and current loops according to the right-hand-rule (right).

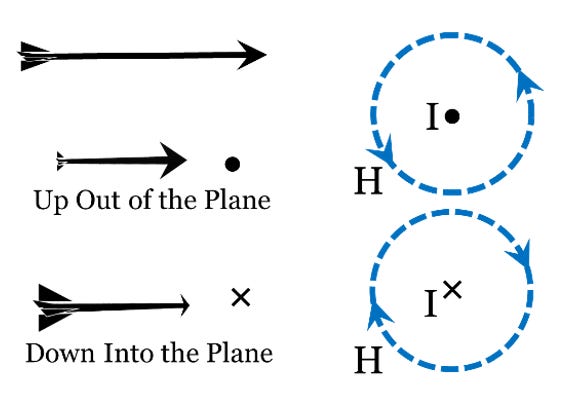
Drawing and comprehending sometimes complicated field distributions in 3-D space can be a challenge. To simplify the portrayal of field distributions, we use “dot-x” notation. Imagine a field line or current segment as an arrow with a pointy tip and four fletches at the tail. If the arrow is coming toward you, up out of the plane of the paper, it will look like a “dot.” If the arrow is pointed away from you, down into the plane of the paper, it will look like an “x.” Thus, the right-hand rule implies a counterclockwise magnetic field around an upward current (dot) and a clockwise magnetic field around a downward current (x). Figure 3.25 shows this geometry.

Figure 3.25: A dot denotes a field line or current traveling up out of the plane; an X denotes a field line or current traveling down into the plane (left). Thus, the magnetic field loops counterclockwise around a current traveling up and clockwise around a current traveling down (right).

Magnetic field lines form rings around a current loop yielding the distinctive patterns that inspired Faraday’s original speculations. Figure 3.25 shows the pattern of magnetic field lines around a current loop (see also Faraday’s result in Figure 3.6). Permanent magnets have their properties because of many such microscopic current loops within their atomic structure. The macroscopic magnetic field patterns generated by permanent magnets follow from the contributions of many small current loops like those of Figure 3.26.

Figure 3.26: Magnetic fields around a current loop, front view (left) and top view (right).

Maxwell’s distinctive contribution was the realization that a changing electric field is equivalent to an extra current or “displacement current.” The displacement current causes an additional magnetic field. An equivalent way to think of it is that a changing current is associated with an extra magnetic field, in addition to the magnetic field of a constant current [[iii]]. This interpretation was popularized by physicist Oleg Jefimenko (1922–2009) [[iv]] but had actually been previously derived [[v]]. There is a simple geometric interpretation as well [[vi]]. When a current changes, it also generates a magnetic field according to the right-hand rule – a radiation magnetic field that propagates away like a ripple on a pond, as in Figure 3.27.

Figure 3.27: An extra (radiation) magnetic field forms around a time-varying current (left). The sense of the magnetic field is given by the right hand rule. The radiation magnetic field ripples out around a changing current as shown in seven time steps (right).

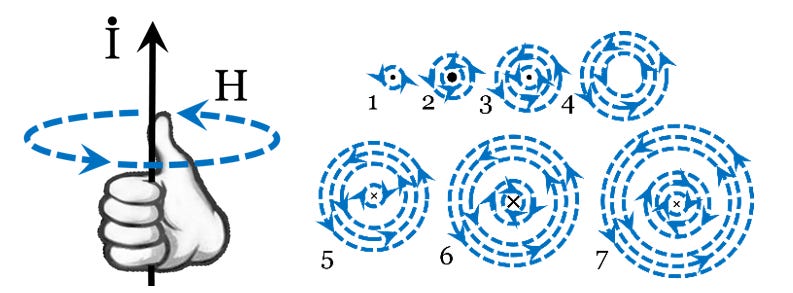
These right-hand rules are fundamental to understanding electromagnetism, so take a moment to align the thumb of your right hand in a particular direction, observe the orientation in which your fingers curl, and compare to Figures 3.25-27.

Maxwell’s displacement current means that a changing electric field or equivalently a changing current creates a magnetic field. This theory provided the first crucial mathematical description for Faraday’s remarkably insightful 1832 comparison of “the diffusion of magnetic forces from a magnetic pole to the vibrations upon the surface of disturbed water….” However, an electromagnetic wave is more than just a magnetic disturbance or an electric disturbance propagating outward. An electromagnetic wave is both of them, working together in a special manner.

Next time, 3.4.5 Faraday’s Law & Electromagnetic Waves: Maxwell’s Theory Suggests Light is an Electromagnetic Wave

---

Follow Online:

You may follow me online in other places as well:

• Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞

• Gab: @aetherczar

• Twitter: @aetherczar

• Amazon: Hans G. Schantz

• Wise of Heart Substack

• ResearchGate

---

References

---

[i] Thumb icon, courtesy Wikimedia. See: https://upload.wikimedia.org/wikipedia/commons/f/fb/Thumbs_up_icon_fixed.png

[[ii]]        Unknown, “Historical Sketch of Electro-magnetism,” Annals of Philosophy, vol. 2, October 1821, p.284: See: https://books.google.com/books?id=rRwp3VVVIbAC&pg=PA468&dq=editions:D0SR3bo-ZUYC&hl=en&newbks=1&newbks_redir=0&sa=X&ved=2ahUKEwjcmPGsveLnAhVLc98KHWRdBNIQ6AEwB3oECD4QAg#v=snippet&q=fig.%2011&f=false

[[iii]]       Griffiths, David J. and Mark A. Heald, “Time-dependent generalizations of the Biot-Savart and Coulomb laws,” American Journal of Physics, Vol. 59, 1991, pp. 111‑117.

[[iv]]        Jefimenko, Oleg D., Electricity and Magnetism, New York: Appleton-Century-Crofts, 1966, §15-7, pp. 515‑518.

[[v]]        Panofsky, Wolfgang K.H., and Melba Phillips, Classical Electricity and Magnetism, 2nd ed., New York: Dover, 2005.

[[vi]]        Schantz, Hans Gregory, “Electromagnetic Radiation Made Simple,” APS/AAPT Joint Meeting, Washington, D. C., April 18-21, 1997.