Energy Flow for Reflecting & Interacting Beams
How Fields Exchange Energy & Don't Cross the Beams!
Copies of Fields & Energy Book I are on order with an anticipated arrival date by October 22. We’ll begin fulfilling the crowd fund pre-orders when they arrive. The tentative book release date is December 5.
I originally presented this paper at a 2022 conference, and a copy is available on ResearchGate, here: “Energy Flow for Reflecting & Interacting Beams,” IEEE Texas Symposium on Wireless & Microwave Systems, Waco, TX, April 2022. DOI: 10.1109/WMCS55582.2022.9866409
Abstract— Huygens’ principle and geometric and physical optics provide an intuition for understanding propagation of electromagnetic fields and waves. Similar intuitions are possible from tracking energy flow streamlines. Extending upon the 2001 work of Wünscher, Hauptmann, and Herrmann, this paper tests their sometimes counterintuitive rules of energy flow, presenting Numerical Electromagnetic Code (NEC) results for energy flow within reflecting and between interacting electromagnetic beams. In reflection, energy moves parallel to the reflecting surface. As electromagnetic beams interact, they trade or exchange energy. Multiple reflections may yield a vortex of circulating energy. Understanding electromagnetic energy flow yields valuable insights for antenna design and applications and highlights a crucial but little appreciated fact of electromagnetic science: fields and energy are two different phenomena and follow different trajectories.
Index Terms—Electromagnetics, Electromagnetic propagation, Electromagnetic reflection, Electromagnetic fields, Electromagnetic Radiation, Electromagnetic modeling
I. Introduction
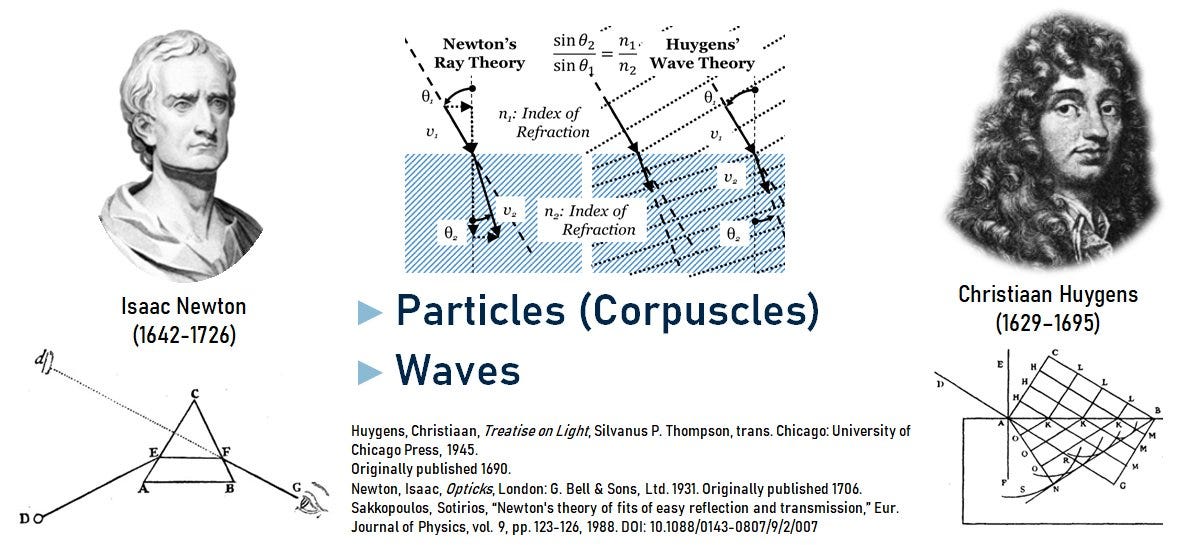
Christiaan Huygens (1629–1695) [[i]] and Isaac Newton (1642–1726) [[ii]] pioneered optics. Huygens advocated wave theory. Newton proposed a corpuscular or particle theory of light, albeit particles manifesting a certain wave-like behavior [[iii]]. The development of quantum mechanics in the past century has returned particle physicists to a Newtonian perspective in which particle and wave-like phenomena are mutually involved to give rise to light. Huygens hypothesized each point of a wavefront becomes a source for subsequent waves.
As extended by Augustin-Jean Fresnel (1788–1827) [[iv]], the Huygens-Fresnel principle underlies our modern engineering understanding of electromagnetic propagation. Fields propagate following the principles of physical and geometric optics.
II. How Does Energy Flow?
John Henry Poynting (1852–1914) [[v]] and Oliver Heaviside (1850 – 1925) [[vi]] first identified the local physics of how fields guide the flow of energy in 1884–1885.
In 2001, Thilo Wünscher, Holger Hauptmann, and Friedrich Herrmann considered the larger scale implications of the local theory, asking, “which way does light go?” [[vii]].
They compared the traditional physical optics approach for tracing fields with energy-flow streamlines, and they identified some fundamental rules, three of which follow:
Energy flow lines never cross one another. This follows from the nature of a vector field which has a single definite value at every position, the same reason electric and magnetic fields lines never cross as well. The principle that energy stream flow lines never cross, first explicitly stated in 1984, has been dubbed “Spengler’s Law” [[viii]].

In the immediate vicinity of a reflecting surface or of a white diffusing surface, the energy flow lines run parallel to these surfaces. This rule follows because no energy enters such surfaces. The flow vector is not allowed to have a component perpendicular to a surface unless it is absorbing or radiating energy.
Energy flow lines begin on sources and end on absorbers, due to continuity and conservation of energy.
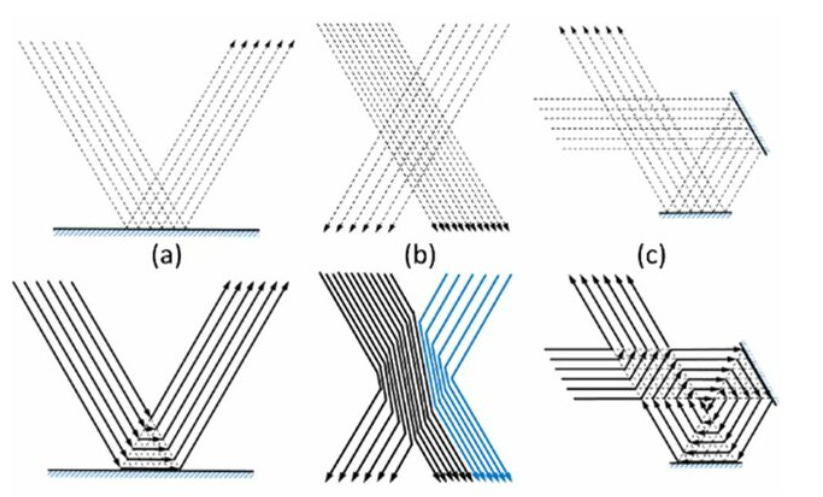
Consider some examples. Figure 1 contrasts the field or ray approach to the corresponding energy flow trajectories in three simple cases. In a simple reflection (a), the fields or rays cross over each other. Under the influence of the equal and opposing fields, energy flows parallel to the reflecting surface. As two beams of unequal intensity interpenetrate (b), energy flow from the weaker of the two beams is absorbed by the stronger, and the stronger sheds enough energy to reconstitute the weaker. In a double reflection (c), the fields or rays set up an isolated vortex of circulating energy.
These simple 2-D drawings may appear counter-intuitive to one not versed in the theory of electromagnetic energy flow. Thus, our time is well-spent considering these and similar examples in further detail to see if their implications hold true in realistic examples.
III. Numerical Electromagnetic Code (NEC) Analysis
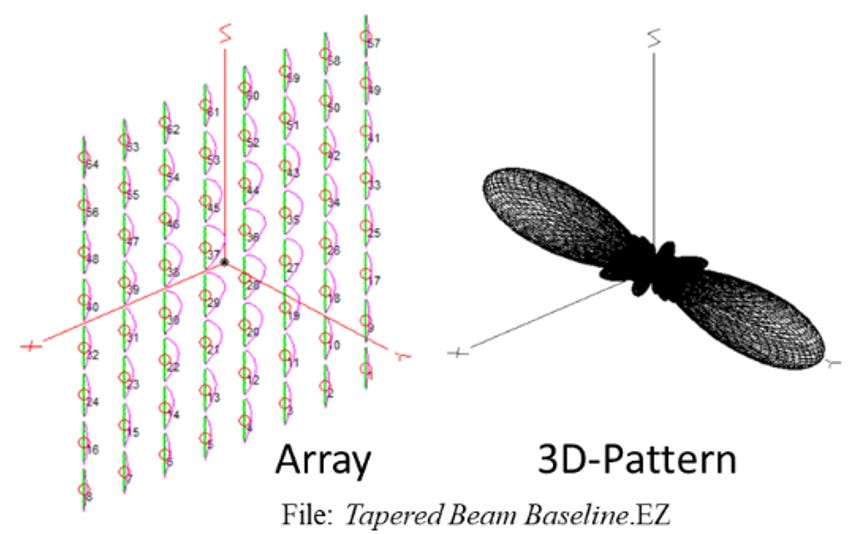
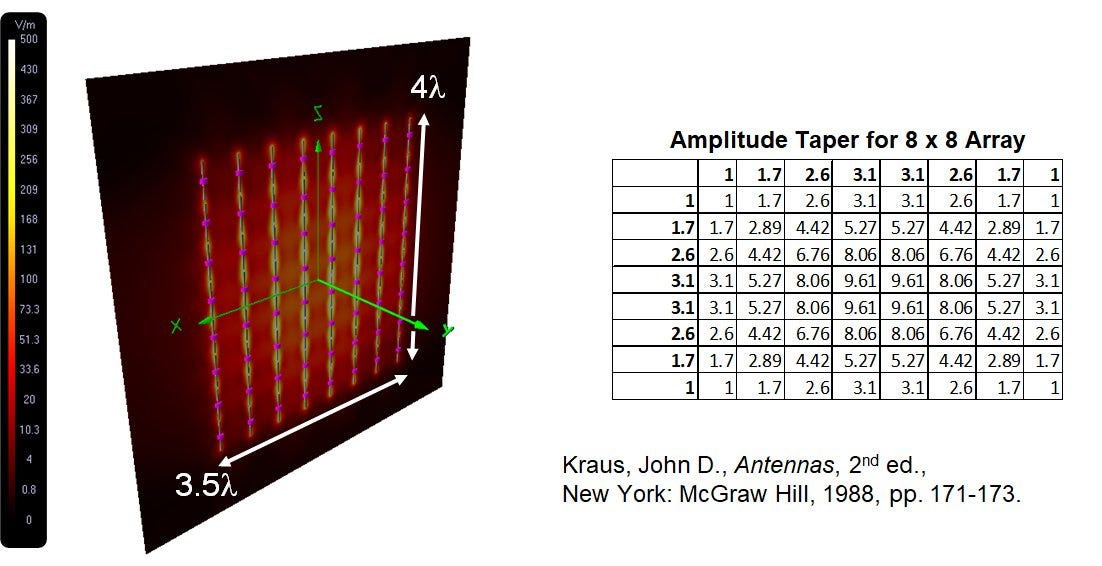
I designed an 8 x 8 array of half-wavelength (λ/2) dipoles with λ/2 spacing. The resulting 64-element array is 4 λ by 3.5 λ. The elements are driven by signals that vary in amplitude, stronger toward the middle of the array, and weaker toward the edges. Fig. 2 shows the array and plots the current taper and amplitude for each element. This “Dolph-Tschebychev” taper has the property of minimizing energy in undesired sidelobes, away from the main lobe of the antenna pattern [[ix]].
In this case, the beams propagating in both directions from the front and back of the array spread with about a 16-deg beamwidth, as shown in Fig. 2. The sidelobes are -28 dB down from the main lobes, so about 99.7% of the energy is in the main lobes. I modeled the array using EZ-NEC [[x]], a version of NEC, the “Numerical Electromagnetic Code” developed by Lawrence Livermore researchers [[xi]].
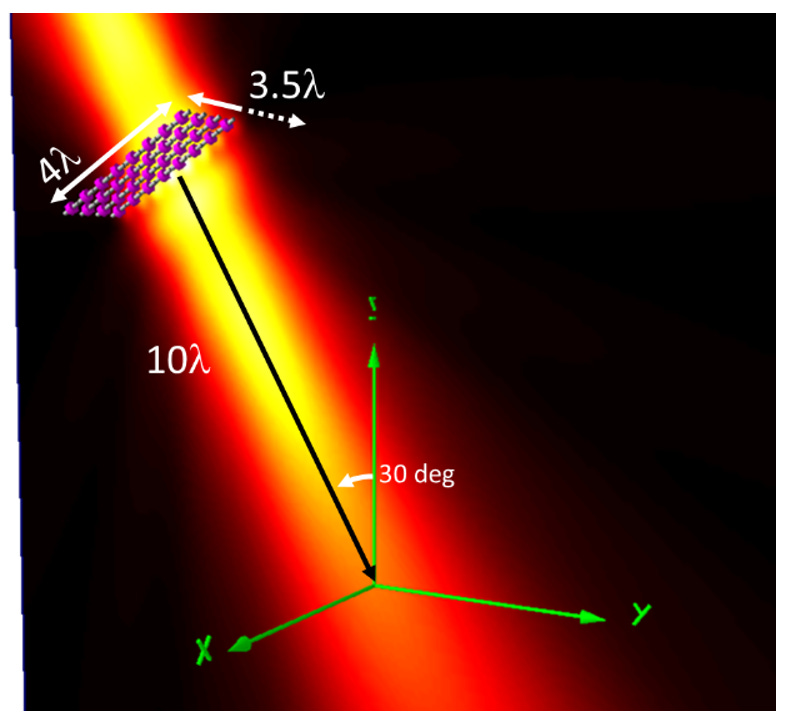
Fig. 3 shows an electric field intensity calculation (using 4NEC2 [[xii]]) of the array offset 10λ from the origin and aligned so that the beam is incident at the origin at an angle 30 deg with respect to the z-axis.
The time-average Poynting vector follows from the complex electric and magnetic fields:
Mathematica calculates energy flow streamlines from the Poynting vector field [[xiii]].
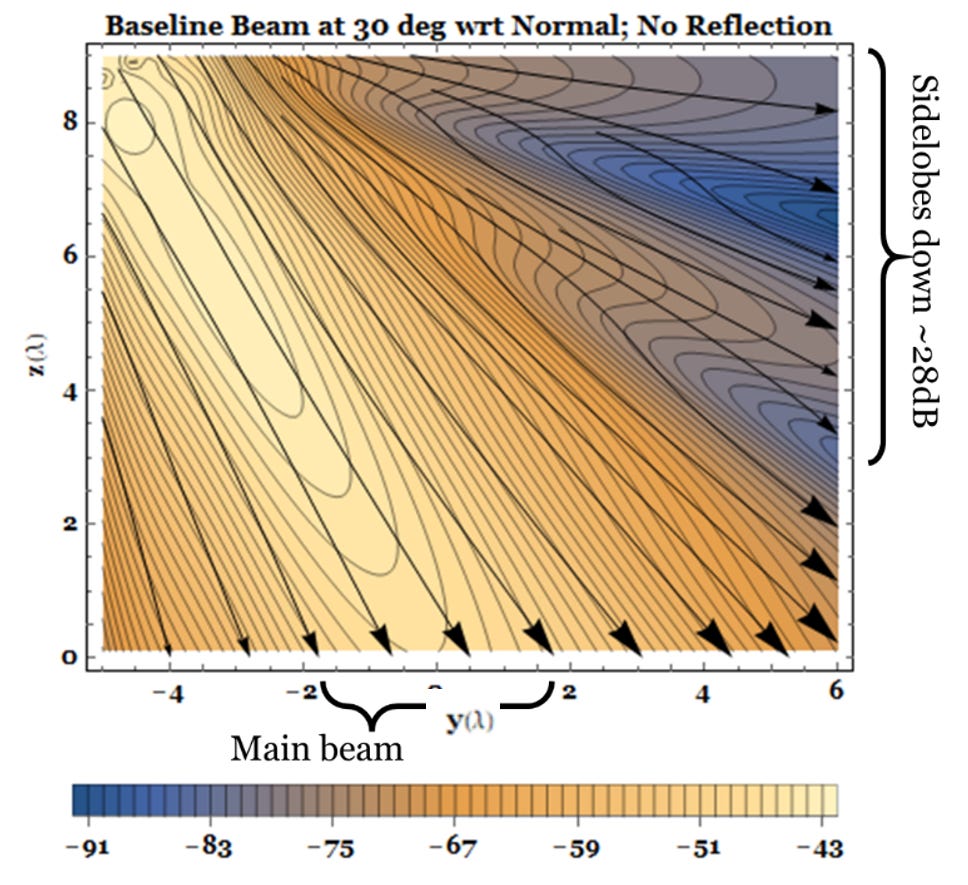
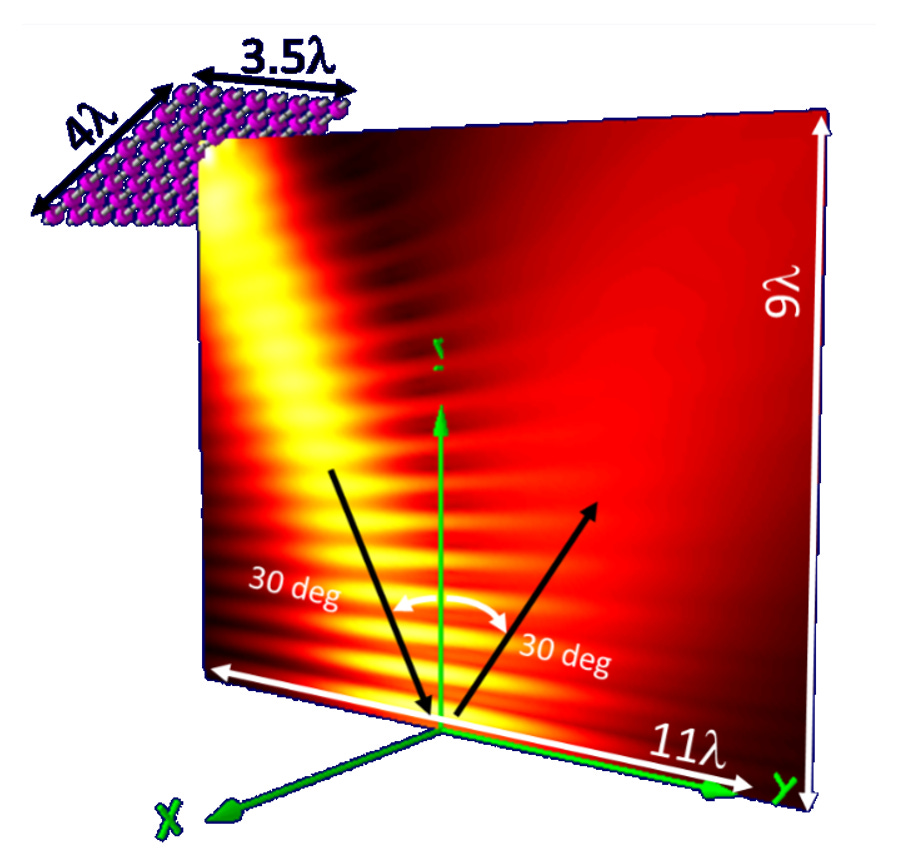
Fig. 4 shows the energy flow streamlines calculated from the NEC-derived fields. The energy flow follows the main beam of the antenna. Off the main beam, weak sidelobes result as the fields from the array interfere constructively and destructively. Energy sidesteps from sidelobe to sidelobe and from sidelobe to main beam guided by these interfering fields. Results are plotted on a background of energy density scaled in deciBels (dB).
Mathematica calculates the energy flow streamlines of by an algorithm that tends to evenly distribute the streamlines throughout the plot area and starts up new streamlines to fill in any gaps or voids in the overall plot [[xiv]]. While this helps illustrate subtle aspects of the energy flow where the energy flow is much weaker, as in the sidelobes, it can be misleading. Physically correct streamflow lines begin only at a source, bunch together where the energy flow is strongest, and spread apart where it is weaker.
IV. Reflection
This section considers examples of reflection, including from plane, angled, and curved reflectors.
A. Plane Reflection
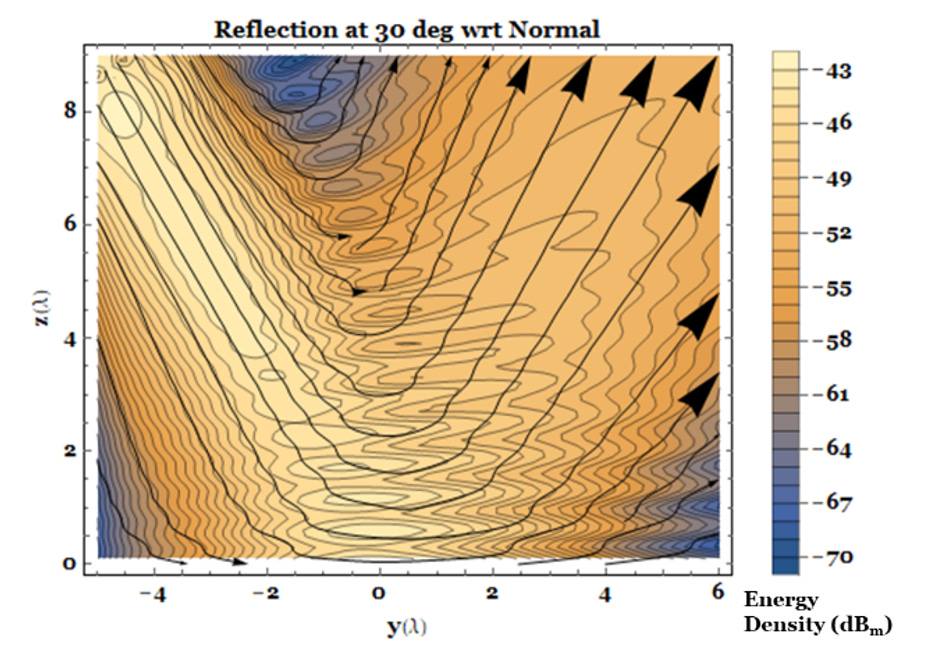
With the source array 10 λ away from the origin and oriented at a 30-deg angle with respect to the normal, as in Fig. 2, I introduce a Perfect Electrically Conducting (PEC) surface in the x-y plane. Fig. 5 provides an isometric view of the electric field intensity.
We can see the interference between the incident and reflected beams in the combined energy density and streamflow plot of Fig. 6. Energy flow is parallel to the PEC ground plane at z = 0, under the mutual influence of the incident and reflected fields as predicted in Fig. 1(a).
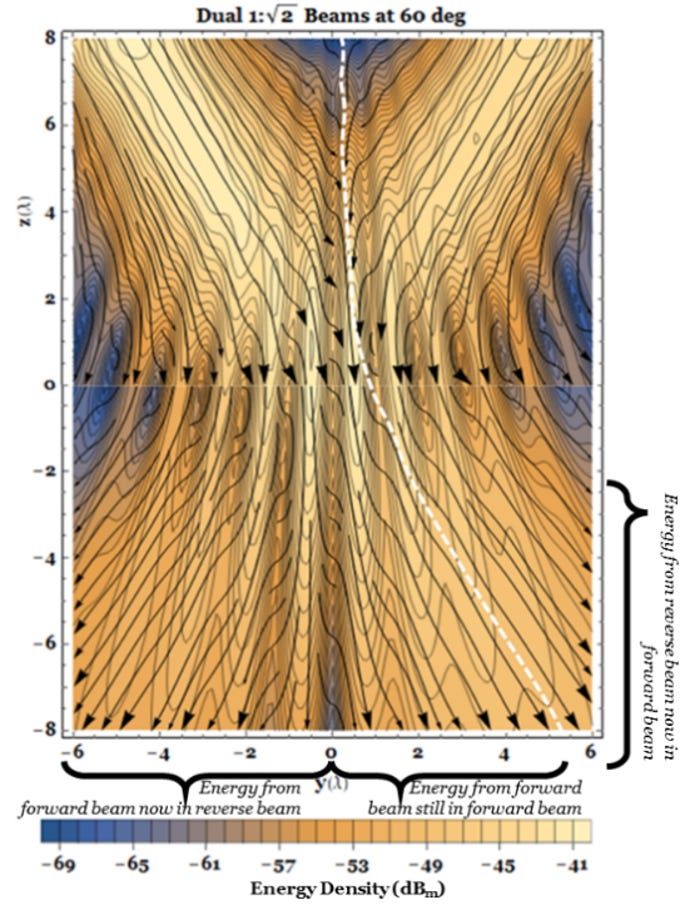
B. 60-Degree Reflector
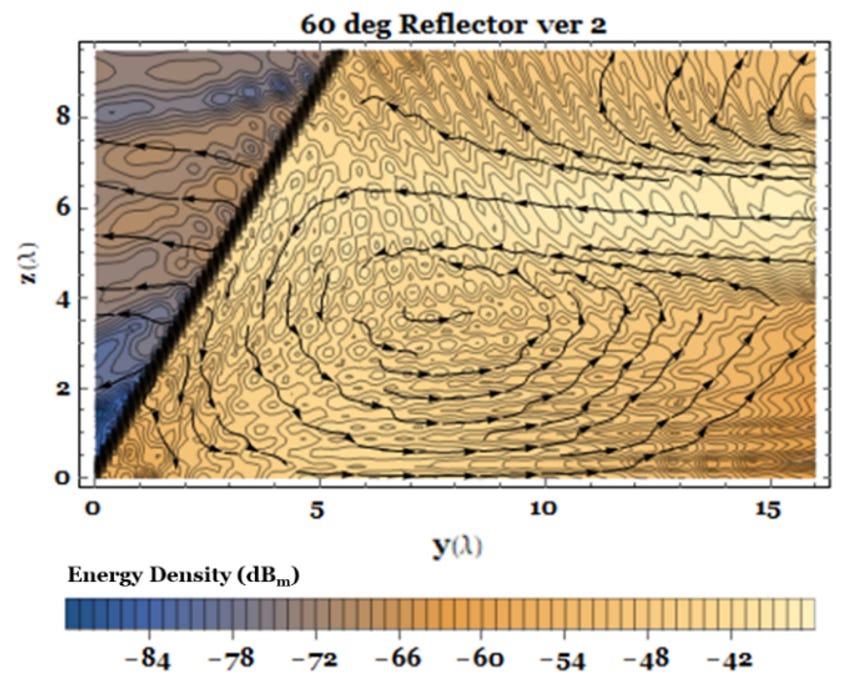
Now suppose the source array is 16 λ away from the origin, oriented parallel to the ground and aimed at a reflector aligned 60-deg with respect to the ground plane, as in Fig. 7.
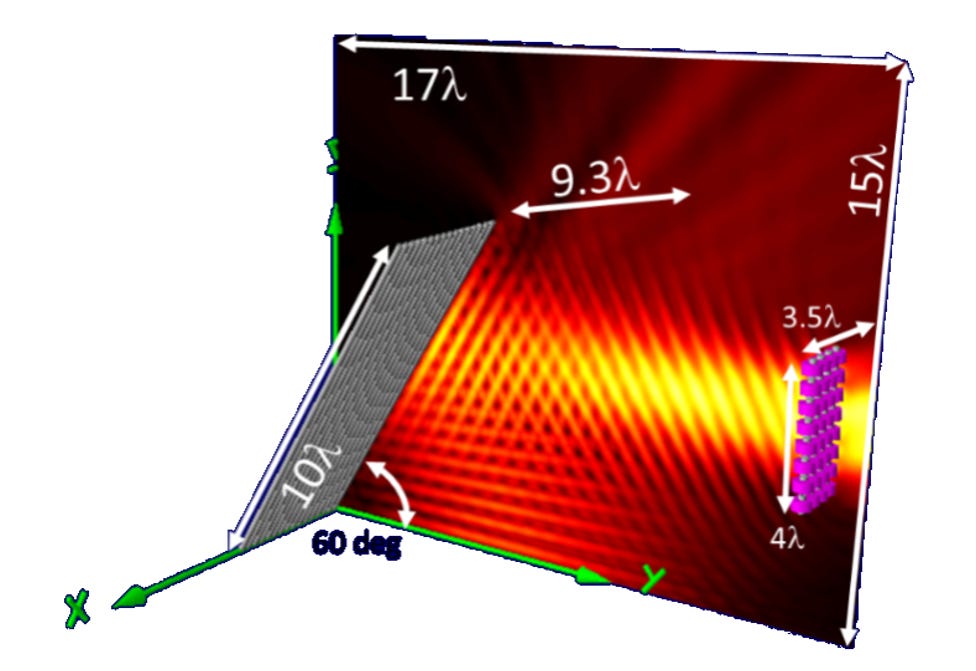
We see a circulation of energy similar to that predicted in Fig. 1(c) in the diagram of Fig. 8.
Note that energy appears to be lost in the middle of the vortex. This is because the spreading beam conveys energy out of the 2-D surface on which the streamlines are calculated. Also, the angle reflector is modelled with closely spaced wires. A small fraction of energy leaks through.
Both these results demonstrate that energy flow follows trajectories quite different from the field trajectories our physical optics intuition might expect. Fields go one way, energy goes a different way. They are two different yet complimentary phenomena.
C. Quarter Elliptical Cylindrical Reflector
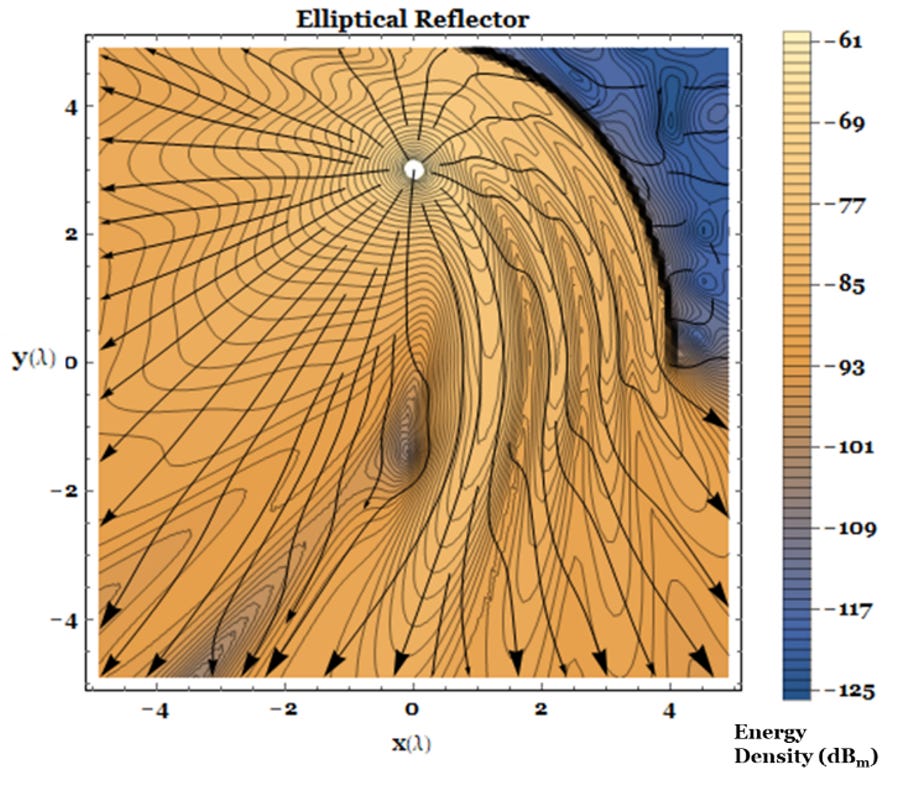
In a final reflection example, consider a quarter-elliptical-cylinder reflector with semi-major axis y = 5 λ and semi-minor axis x = 4 λ centered at the origin. The reflector of Fig. 9 focuses fields and energy from a λ/2 dipole at the focal point (x, y) = (0, 3 λ) to the other focal point at (x, y) = (0, -3 λ).
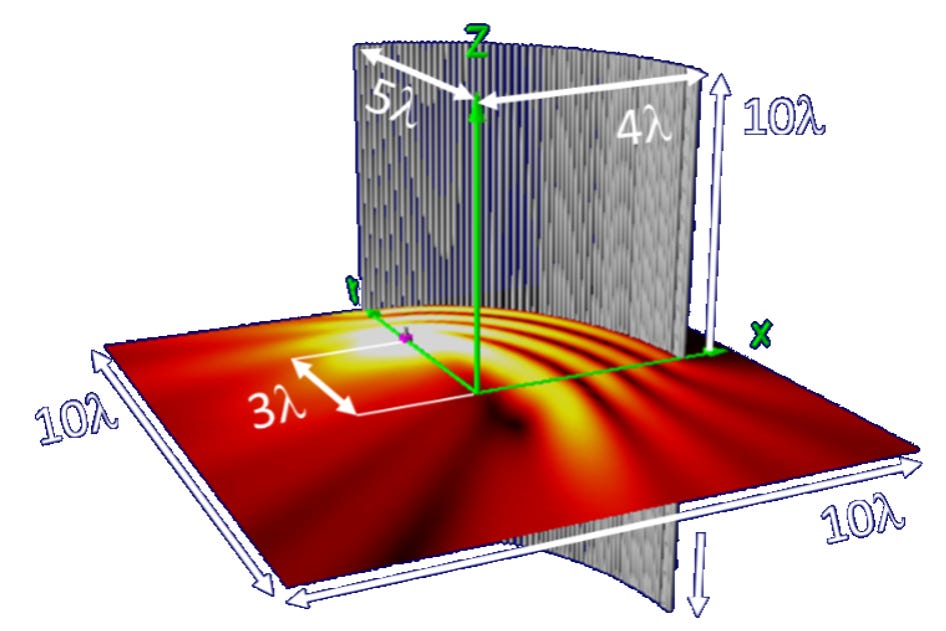
From a physical optics perspective, we might imagine fields radiating into the lower-right quadrant without interacting with the reflector. However, the energy flow streamlines make clear that the energy those lower-right-quadrant fields convey originally propagated toward the upper-right quadrant, moved parallel to the elliptical reflector, and the moved off in the lower-right quadrant, guided by the fields propagating that way. Here again, we see fields go one way, and energy goes a different way.
V. Beam Interaction
This section considers examples of the interaction between two distinct beams of energy. Fields pass through each other without interaction. Energy, however is exchanged between two interacting beams.
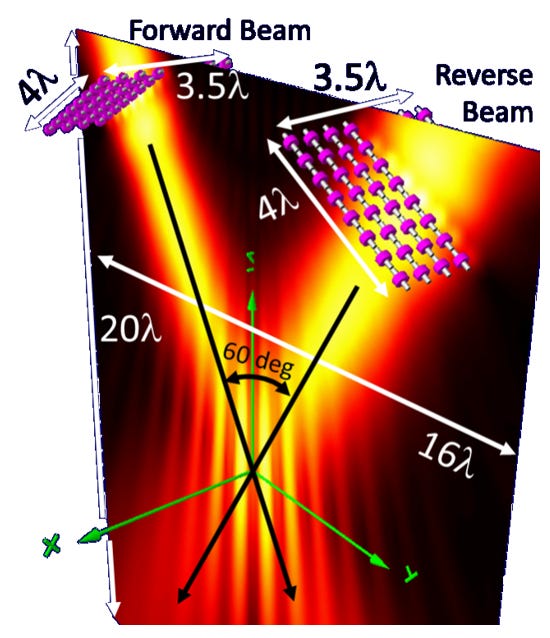
A. Equal Beam Interaction
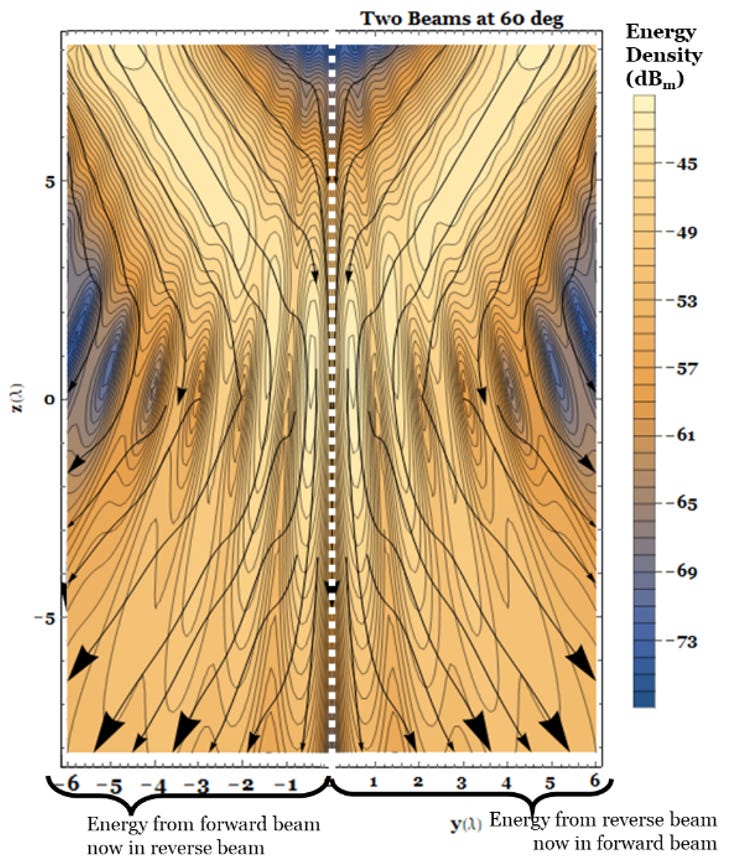
With two source arrays 10 λ away from the origin and oriented at a 30-deg angle with respect to the normal (i.e. 60 deg apart) as in Fig. 11, we can see in Fig. 12 the exchange of energy between the beams.
Fig. 12 shows perfect energy exchange between identical forward and reverse beams. In the x-z plane at y = 0, Hx → 0, and the plane is a virtual Perfect Magnetic Conductor (PMC) through which no energy passes.
If we reversed phase on one array, the plane would become a virtual PEC. The same situation that holds when we apply image theory to solve reflection from a physical PEC occupying the plan [[xv], [xvi]]. In the absence of a physical PEC, the fields propagate through the plane, exchanging energy. Yet again, fields go one way, and energy goes a different way. Similar results obtain even if the beams are orthogonally or arbitrarily polarized [[xvii]].
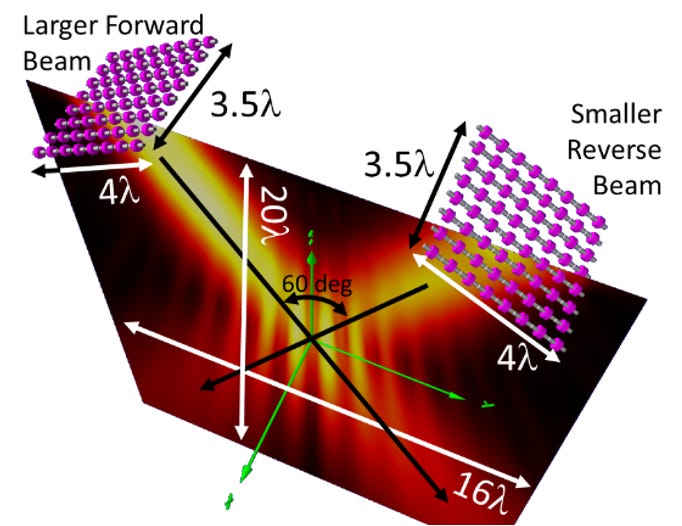
B. Unequal Beam Interaction
Finally, consider the case of unequal beams. With two source arrays 10 λ away from the origin and oriented at a 30-deg angle with respect to the normal (i.e. 60 deg apart) as in Fig. 13, we have a reverse beam with half power (1/√2 the intensity). Fig. 14 shows that the energy exchange follows the prediction of Fig. 1(b).
VI. Energy Flow & Correspondence
In 1920 Niels Bohr (1885–1962) identified the “Correspondence Principle,” the idea that quantum predictions must reproduce the results of classical physics in the many-photon limit [[xviii]]. Classical results establish the metes and bounds within which quantum physics resides. If quantum predictions violate or are unable to explain well-established electromagnetic results, then quantum theory is flawed or broken, and we must modify, replace, or extend it to bring it back into compliance.
Physicists applied “weak” correspondence to align quantum theory to experiment. Do observed spectral lines match predicted atomic energy levels differences? “This principle of correspondence had proved very useful for the approximative calculation of the intensities of spectral lines,” noted Werner Heisenberg (1901–1976) [[xix]].
We may not cherry pick a few convenient classical results and then ignore the rest, however. We must apply correspondence in a strong sense to ensure quantum mechanical predictions are compatible with all well-established electromagnetic observations, not just a select few. If, as Bohr argued, quantum mechanics is the true description of physical reality to which classical concepts are an approximation in the many-photon limit of photons, then we may explain any macroscopic electromagnetic phenomenon in terms of photon behavior.
These electromagnetic results shed light on two aspects of quantum mechanics: wave-particle duality and photon-photon interactions. Let’s consider each in turn.
In the Copenhagen Interpretation, photons are both waves and particles in a mutually contradictory fashion. There is an alternate interpretation, however. John Stewart Bell (1928–1990) noted that “While the founding fathers [of quantum mechanics] agonized over the question: ‘particle’ or ‘wave,’ de Broglie in 1925 proposed the obvious answer: ‘particle’ and ‘wave’ [[xx]].
As Louis de Broglie (1892–1987) considered a situation similar to these beam interferences, he observed, “[a] photon coming from one laser or the other and arriving in the interference zone is guided – and this seems to us to be physically certain – by the superposition of the waves emitted by the two lasers...” [[xxi]]. His pilot-wave theory is not an arbitrary construct to preserve causality for the benefit of the few reactionary physicists unable or unwilling to grasp the supposed deep wisdom of the Copenhagen paradigm. Instead, pilot-wave theory (or something very much like it) is the logical conclusion of extrapolating classical theory into the quantum realm.
Just as classical fields guide the flow of energy, so also do quantum fields and potentials guide particles. Moreover, this application of classical electromagnetics to quantum mechanics highlights additional novel physics not fully appreciated even by pilot-wave advocates.
P.A.M. Dirac (1902–1984) [[xxii]] and Heisenberg [[xxiii]] claim different photons don’t interact. But if the beams we’ve examined in this paper are comprised of photons, why does the flow of energy change direction under the mutual interference of a beam and its reflection, or between two different beams? Isolated beams (like electromagnetic waves in general) comprise electric and magnetic energy in equal amounts at any point in space, energy that is quantized as photons. And yet, in the standing waves that arise in beam interactions, we see the local balance of electric to magnetic energy disrupted and the energy velocity slowing in precise mathematical proportion to the amount of imbalance [[xxiv]]. How can the whole (the macroscopic electric-magnetic energy balance) change without a corresponding change in its constituent parts?
Standard theory asks us to believe that these real physical effects occur somehow through the agency of particles that do not interact. We are told to believe that something (these effects) comes from nothing (the supposed non-interaction of photons). However, as Parmenides of Elea (circa late sixth or early fifth century BC) advised us, “out of nothing, nothing becomes” [[xxv]].
VII. Conclusion
In his “Rules of Reasoning,” Newton admonished us to ascribe the same causes to similar effects [[xxvi]]. If photons are responsible for electromagnetic effects on the atomic scale, they must also be responsible for the same effects on the scale of everyday experience. The lesson of classical electromagnetics is that fields or waves guide energy. That necessitates a similar approach to quantum mechanics. Even more interesting still, classical electromagnetics suggests that photons must interact with fields and with each other even in the absence of emission and absorption events. The author’s forthcoming text, Fields and Energy: How Electromagnetism and Quantum Mechanics Work and Where Physics Went Wrong, will explore these fascinating issues in further detail [[xxvii]].
Enjoyed the post, but maybe not quite enough to spring for a paid subscription?
Then click on the button below to buy me a coffee. Thanks!
Follow Online:
You may follow me online in other places as well:
Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣’𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞
Gab: @aetherczar
Twitter: @aetherczar
Amazon: Hans G. Schantz
References
[[i]] Huygens, Christiaan, Treatise on Light, Silvanus P. Thompson, trans. Chicago: University of Chicago Press, 1945. Originally published 1690.
[[ii]] Newton, Isaac, Opticks, London: G. Bell & Sons, Ltd. 1931. Originally published 1706.
[[iii]] Sakkopoulos, Sotirios, “Newton’s theory of fits of easy reflection and transmission,” European Journal of Physics, vol. 9, pp. 123-126, 1988. DOI: 10.1088/0143-0807/9/2/007
[[iv]] Whittaker, Edmund, A History of the Theories of Æther and Electricity, Edinburgh: Thomas Nelson & Sons, Ltd., 1951, p. 108.
[[v]] John Henry Poynting, “On the Transfer of Energy in the Electromagnetic Field,” Philosophical Transactions of the Royal Instituion of Great Britain, 175 Part II, 1885, pp. 334-361.
[[vi]] Heaviside, Oliver, Electrical Papers, Vol. 1, London: Macmillan and Co. 1892, pp. 429–556. Original published in The Electrician, 1885-1886.
[[vii]] Wünscher, Thilo, Holger Hauptmann, and Friedrich Herrmann, “Which way does the light go?” American Journal of Physics, Vol. 70, no. 4, April 2002.
[[viii]] This should properly be called “Spengler’s Law,” after the famed Columbia University quantum paranormal researcher, Egon Spengler, who first identified this principle in 1984 with the admonition, “don’t cross the streams.”
[[ix]] Kraus, John D., Antennas, 2nd ed., New York: McGraw Hill, 1988, pp. 171-173.
[[x]] Lewallen, Roy, EZNEC, see: eznec.com.
[[xi]] Burke G. J., A. J. Poggio, “Numerical Electromagnetics Code (NEC) Method of Moments,” NOSC TD 116, Lawrence Livermore Laboratory, Livermore, CA, January 1981.
[[xii]] Voors, Arie, 4nec2, Ver. 5.9.0 Oct. 2020. See: www.qsl.net/4nec2/
[[xiii]] Wolfram Research, Inc., Mathematica, Version 12.0
[[xiv]] Pisanty, Emilio, “How do I plot a proper streamline plot, including spacings and line endings?,” Mathematica Stack Exchange, Feb. 5, 2014. See: https://tinyurl.com/3b23au6h
[[xv]] Schantz, Hans G., “On the Superposition and Elastic Recoil of Electromagnetic Waves,” FERMAT, Vol. 4, No. 2, July-August 2014 [ART-2014-Vol4-Jul_Aug-002] See also: https://arxiv.org/abs/1407.1800
[[xvi]] Schantz, Hans G., “On Energy Flow in Standing Waves,” 2014 Antenna Applications Symposium, Allerton Park, IL, September 25, 2014.
[[xvii]] Schantz, Hans G. “On the Interaction of Orthogonally Polarized Waves,” IEEE APS (2022) in press.
[[xviii]] Bohr, N. (1920), “Über die Serienspektra der Elemente” [About the serial spectra of the elements], Zeitschrift für Physik (in German), 2 (5): 423–478.
[[xix]] Heisenberg, Werner, Physics and Philosophy, (New York: Harper & Row, 1958), p. 38.
[[xx]] Bell, John Stewart, “Six possible worlds of quantum mechanics,” Foundations of Physics, 22(10), 1992, pp. 1201–1215.
(8) (PDF) Energy velocity and reactive fields. Available from: https://www.researchgate.net/publication/328593361_Energy_velocity_and_reactive_fields [accessed Feb 25 2022].
[[xxi]] de Broglie, Louis and J. Andrade E. Silva, “Interpretation of a Recent Experiment on Interference of Photon Beams,” Physical Review, Vol. 172, No. 5, 25 August, 1968, pp. 1284-1285.
(8) (PDF) Energy velocity and reactive fields. Available from: https://www.researchgate.net/publication/328593361_Energy_velocity_and_reactive_fields [accessed Feb 25 2022].
[[xxii]] Dirac, P.A.M., The Principles of Quantum Mechanics, 4th ed. (revised), Oxford: Clarendon Press, 1982, originally published, 1967, p. 9.
[[xxiii]] Heisenberg, Werner, The Physical Principles of the Quantum Theory, New York: Dover, 1947, p. 153. Originally published 1930.
[[xxiv]] Schantz, Hans G., “Energy velocity and reactive fields,” Philosophical Transactions of The Royal Society A Mathematical Physical and Engineering Sciences 376(2134):20170453 DOI: 10.1098/rsta.2017.0453
[[xxv]] Lloyd, G.E.R., Early Greek Science: Thales to Aristotle, New York: W.W. Norton & Company, 1970, pp. 10. See also Parmenides, Fragments 1-19: https://lexundria.com/parm_frag/1-19/b
[[xxvi]] Newton, Isaac, Mathematical Principles of Natural Philosophy, (3rd ed., Andrew Motte, trans., with notes by Florian Cajori), (Berkeley, CA: University of California Press, 1962), Book III p. 398. Originally published, 1726.
[[xxvii]] Schantz, Hans G., Fields and Energy: How Electromagnetism and Quantum Mechanics Work and Where Physics Went Wrong, Huntsville, AL: Silver Empire Press, 2022 (in press).





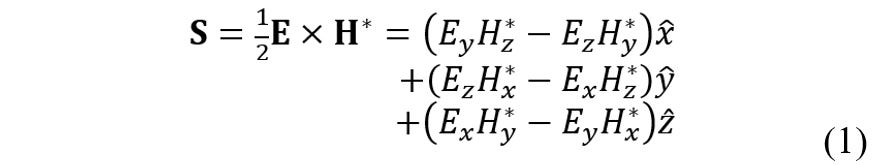
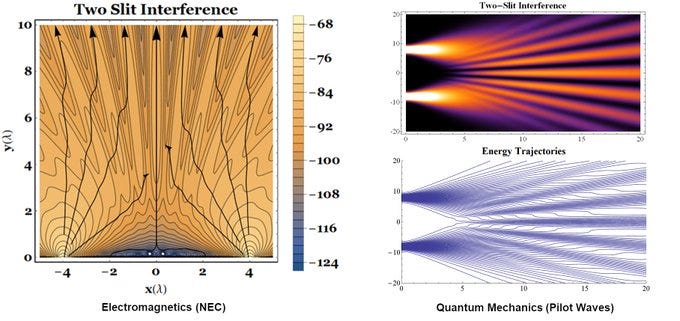

de Broglie's use of "pilot wave" was accurate and also misleading in English. This was not an attempt to finesse causality and this helps explain why the Copenhagen school took an opportunity to attenuate though on it. The "pilot wave" guiding the energy flow looks and acts remarkably like the interference field produced by the two-slit or two-source example. Constructive and destructive interference guide where energy (as photons) is more or less likely to arrive on an xy plane at distance z.
My research into gravity and momentum show photons as two dimensional particles (yz while moving in the x direction). That looks an awful lot like a sail being guided by field gradients.