2.6 Isaac Newton

An Introduction to a Founding Father of Physics

The discoveries of Galileo and Kepler in turn provided a foundation for Isaac Newton (1642–1727) to discover his Laws of Motion and his Law of Universal Gravitation. The story is more complicated than merely an apple impacting Newton’s occiput.

Might the moon be falling toward the Earth in the same way an apple falls to the ground? Using the experimental data available to him, Newton calculated that the ratio of the moon’s acceleration to the acceleration of an object falling near the surface of the earth was roughly equal [[iii]] to the inverse ratio of their distances from the center of the earth, squared. This suggested that the gravitational force decreased as the inverse square of the distance.

Figure 2.26: Isaac Newton (1642–1727) [[i]], left, connected the terrestrial motion of ballistics with the celestial motion of orbits using his Law of Universal Gravitation [[ii]], right.

Under the assumption of this inverse square relationship, the terrestrial parabolic ballistic motions transition seamlessly to the elliptical orbits of the planets. Newton imagined a cannon on top of a high mountain as in Figure 2.26. At low velocities, the trajectory of a projectile follows a parabolic path (A, B). At a high enough velocity (ignoring any air resistance), the projectile falls toward the Earth at the same rate as the Earth curves beneath it. The result is a circular orbit (C). At higher velocities, the orbit is elliptical (D). At still higher velocities, the projectile exceeds “escape velocity” and follows a hyperbolic path away from the Earth (E).

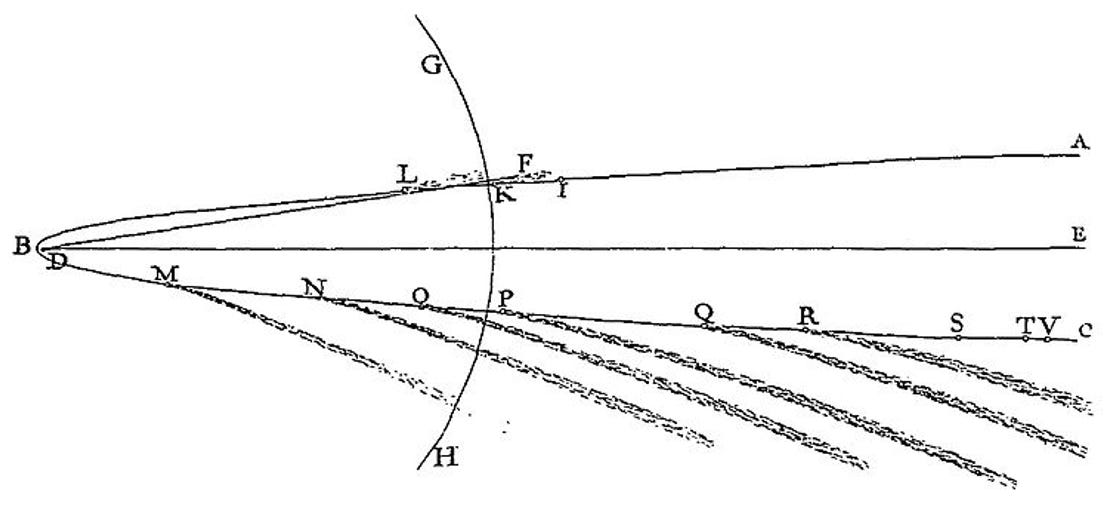
Newton continued his investigations. Under the assumption of point bodies and circular orbits, Newton found his law would also yield the appropriate relation between the period of the orbit and the size of the orbit discovered by Kepler. Real planetary orbits are more complicated than perfect circles, though. Newton was aware of Kepler’s discovery that planetary orbits are elliptical. Newton demonstrated through a lengthy geometric proof that his inverse square law would yield Kepler’s relation even in the case of elliptical orbits, thus tying his abstract ideas back to physical reality [[v]]. He even used his own and others’ observations of the Great Comet of 1680 to verify Kepler’s Laws, as Figure 2.27 depicts.

Figure 2.27: Newton used his own and others’ observations of the Great Comet of 1680 to calculate the comet’s orbit and validate Kepler’s Laws of Planetary Motion [[iv]]. Note, this wasn’t what would come to be known as Halley’s Comet which appeared in 1682.

Finally, real planets are not point masses. Instead, their mass is distributed throughout an extended body. Newton showed that the gravitational attraction of a spherically symmetric body was the same as the attraction of a point object with the same mass [[vi]]. To do so, he had to invoke what were for the time very sophisticated and abstract mathematical ideas, like an infinite sum of infinitesimals, a basic idea in calculus (of which Newton was the co-inventor with Gottfried Wilhelm von Leibniz (1646–1716)). Newton’s concept of a point mass was thus an idealization that he firmly grounded in reality.

Next time, a discussion of Newton’s methods, followed up by posts on Newton’s legacy, and the misinterpretation of what Newton had to say.

---

Follow Online:

You may follow me online in other places as well:

• Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞

• Gab: @aetherczar

• Twitter: @aetherczar

• Amazon: Hans G. Schantz

• Wise of Heart Substack

• ResearchGate

  ---

References

---

[i] https://pixabay.com/vectors/isaac-newton-portrait-vintage-3936704/

[ii] Brian Brondel, after an original diagram by Newton. https://commons.wikimedia.org/wiki/File:Newton_Cannon.svg

[iii] To within about 11%.  Discouraged by the discrepancy, Newton set aside his calculation for several years, until he learned of a different more accurate value for the earth-moon separation.  The agreement using this value was near exact.

[iv] Newton, Isaac, Mathematical Principles of Natural Philosophy, (3^rd ed., Andrew Motte, trans., with notes by Florian Cajori), Berkeley, CA: University of California Press, 1962, Book III Proposition XLI, Problem XXI, pp. 519. Originally published, 1726. See: https://commons.wikimedia.org/wiki/File:Newton_Comet1680.jpg

[v] Newton, Isaac,  Mathematical Principles of Natural Philosophy, (3^rd ed., Andrew Motte, trans., with notes by Florian Cajori), (Berkeley, CA: University of California Press, 1962), Book I §III pp. 56-67.  Originally published, 1726.

[vi]  Isaac Newton, Op.Cit.  Book I §XII, p. 193-213.