Near-Field Technology - An Emerging RF Discipline

How Does My 2006 Paper Hold Up?

In 2006, I was invited to Nice, France to deliver one of the two keynote addresses at the first European Conference on Antennas and Propagation (EuCAP). The topic I chose was Near-Field Technology - An Emerging RF Discipline, and with some contributions from my colleague, James Fluhler, I drafted this paper. In republishing it here, I corrected a few typos I spotted. Also, I added an afterward to share my thoughts on how well my predictions held up.

ABSTRACT

This paper explains and surveys the emerging RF discipline of near-field technology. First, this paper defines what is meant by the “near field.” Then, this paper presents a brief history of near-field technology from Faraday to the present day. In particular, this paper focuses on recent advances in near-field technology for applications like Near Field Communications (NFC), Radio Frequency Identification (RFID), and Real Time Location Systems (RTLS). Finally, this paper will discuss the extension of propagation laws and antenna gains to the near-field regime.

1. INTRODUCTION

The “leading edge” of radio frequency (RF) practice moves to increasingly higher and higher frequency in lock step with advances in electronics technology. The most commercially significant RF systems are those operating at microwave frequencies and above, such as cellular telephones and wireless data networks. Microwave frequencies have the advantage of short wavelengths, making antenna design relatively straightforward, and vast expanses of spectrum, making large bandwidth, high data rate transmissions possible.

There are many applications, however, that do not require large bandwidths. These include radio frequency identification (RFID) systems, real time locating systems (RTLS) and low data rate communications systems, such as hands free wireless mikes or other voice or low data rate telemetry links. For applications like these, lower frequencies have great utility:

• Lower frequencies tend to be more penetrating than higher frequencies.

• Lower frequencies tend to diffract around objects that would block higher frequencies.

• Lower frequencies are less prone to multipath.

• Lower frequencies roll-off more quickly than higher frequencies allowing relatively small cell sizes and more efficient re-use of spectrum.

An amazing and often overlooked world of RF phenomena lies within about a half wavelength of an electrically small antenna. This realm is known as the “near-field zone.” The near-field zone is usually neglected by RF scientists and engineers because typical RF links operate at distances of many wavelengths where near-field effects are utterly insignificant. “Near- field” means different things in different contexts. Fortunately there is an excellent article available that sorts through the various definitions of near-field and provides some guidance [1]. Harold Wheeler introduced the classic definition of the “radiansphere” to denote the boundary between near- and far-field regions [2]. The radiansphere is a spherical shell of radius λ/2π around a small dipole antenna. This is the distance at which the induction and radiation terms are equal in magnitude. Inside, the induction terms dominate. Outside, the radiation terms dominate. Although the radiation terms dominate outside the radiansphere, the induction terms still play a significant role out to a half-wavelength or even farther.

First, this paper will present a brief history of near-field technology from Faraday to the present day. In particular, this paper focuses on recent advances in near-field technology for applications like Near Field Communications (NFC), Radio Frequency Identification (RFID), and Real Time Location Systems (RTLS). Finally, this paper will discuss the extension of propagation laws and antenna gains to the near-field regime.

2. NEAR-FIELD WIRELESS: A BRIEF HISTORY

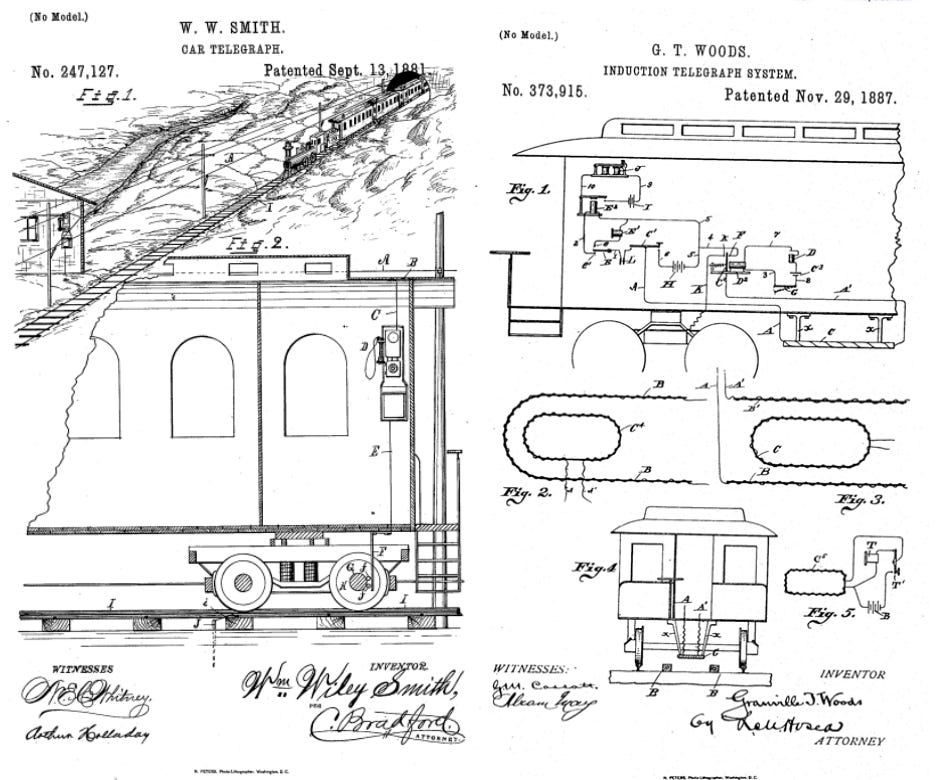
Micheal Faraday (1791-1867) and Joseph Henry (1797-1878) independently discovered induction in the 1830’s. Since Faraday was the first to publish, he is generally given credit for the discovery. Faraday’s work led not only to Maxwell’s Equations, but also to applications including electric motors and electric generators. Understanding induction also led to the discovery of a practical system of telegraphy. The first commercial “wireless” systems were actually near-field or inductive coupled systems that allowed operators on board a train to communicate using a telegraph wire parallel to the train track. In fact, the first induction wireless system was patented by William Smith in 1881 [3]. Granville T. Woods also patented a more practical induction telegraph in 1887 [4]. Neither scheme enjoyed any significant commercial success, however. Figure 1 shows the cover pages of these patents.

Figure 1: The induction wireless systems of Smith [Ref. 3] (left) and Woods [Ref. 4] (right).

As technology progressed and as the discoveries of Hertz, Lodge, and Marconi shifted interest to long distance communication, near-field wireless was largely ignored in favor of far-field wireless. In his 1932 text, Radio Engineering, Frederick Emmons Terman famously observed, “An understanding of the mechanism by which energy is radiated from a circuit and the derivation of equations for expressing this radiation quantitatively involve conceptions that are unfamiliar to the ordinary engineer [5].” If the application of Maxwell’s equations to far-field radiation problems was beyond practical everyday engineers, the further subtleties of near-field phenomena were even more arcane and esoteric.

By the time of the Second World War, radio engineering experienced a renaissance. Maxwell’s Equation assumed their rightful place as the foundation of RF engineering, and RF engineering became not only an art but also a science. Interest in microwaves for radar applications pushed RF technology to such high frequencies that near-field RF remained a neglected and poorly understood backwater. Still, radar technology also introduced the concept of reflecting RF energy from a passive target, even using the reflected power as a communications medium [6].

Now with rapidly growing demands for short range communications links, non-line-of-sight inventory control, and real-time location information, near-field wireless is emerging as the best solution to a variety of significant problems.

3. THE NEAR-FIELD INDUSTRY

Near-field RF technology is applicable in a number of important applications. This section will survey the use of near-field RF for short range communications, for inventory control using passive tags (RFID), and for Real-Time Locating Systems (RTLS).

3.1 Near Field Communication

Aura Communications was formed in 1995 to exploit near-field behavior in the context of short-range communication systems including wireless hands-free earpieces and headphones [7] (see Figure 2).

Figure 2: Freelinc earpiece incorporating near-field magnetic induction technology [Ref. 7].

Aura Communications “LibertyLink™” magnetic induction data transfer system provides 410kb/s data rates at 3m ranges operating at 13.56 MHz. Sony, Nokia, and Phillips teamed to form the Near-Field Communication (NFC) Forum, to promote similar technology [8]. In 2003, a global standard for near-field communication was adopted [9]. Key applications are anticipated to include contactless payments, secure verification and validation, and hands-free earpieces and headphones.

3.2 Radio Frequency Identification (RFID)

In the 1960’s companies like Checkpoint systems, Inc. [10] and Sensormatic [11] introduced Electronic Article Surveillance (or EAS) systems. These “one-bit” tags are used for inventory control and deterrence and detection of shoplifters. With typical ranges of 1-3m (3-10ft), RFID technology as currently practiced today goes back at least to the early 1970’s. Martin Cardullo was awarded a patent in 1973 for a passive transponder capable of modulating a reflected signal with stored data (see Figure 3) [12].

Figure 3: Cardullo’s 1973 patent described an RFID tag [Ref. 12].

Additional information and references pertinent to the development of RFID are available in an online article [13]. The burgeoning area of RFID technology exploits near-field physics to enable short-range, low-cost tags with the potential to revolutionize supply-chain management and inventory control. With the recent adoption by WalMart and other large retailers of RFID technology, this alone promises to be a $5 billion industry by 2007 [14]. Figure 4 shows a typical RFID tag used in an Electronic Product Code (EPC) application.

Figure 4: Modern Electronic Product Code (EPC) RFID tag [Ref. 15].

3.3 Real-Time Location Systems (RTLS)

Near-field behavior is also the foundation for a breakthrough in wireless tracking and positioning pioneered by the Q-Track Corporation [note, I was a co-inventor of the technology, co-founder of the company, and served as CTO]. “Near-field electromagnetic ranging” or NFER™ technology allows for positioning with an accuracy approaching one foot at ranges up to 250 feet or more, even in complicated indoor propagation environments [16]. Figure 5 shows a tag, receiver, and tracking GUI for this system.

Figure 5a (left): Q-Track’s evaluation kit (EVK) personal tag transmitter. Figure 5b (center): Q-Track’s evaluation kit (EVK) locator receiver with receive antenna array. Figure 5c (right): Q-Track’s tracking software displays the location of a mobile transmitter. Accuracy is typically within 30cm (1ft) at ranges up to 70m (250ft) for a calibrated system [© 2006; Q-Track Corporation].

The emerging near-field industry is poised for explosive growth, but places unique demands on antenna (or sensor) technology. Near-field sensors and tags are generally not characterized with respect to gain, so there is no way for engineers to mathematically define or evaluate a link equation. The near-field industry relies on trial-and-error and empirical approaches to antenna design [17]. There is a significant disconnect between theory and practice which means there are similarly significant opportunities for engineers and scientists in both industry and academia.

4. NEAR-FIELD ANTENNAS AND PROPAGATION

The dipole field equations provide a relatively simple model of near-field behavior. A small electric antenna (like a whip) is modeled by an electric dipole and a small magnetic antenna (like a loop or loopstick) is modeled by a magnetic dipole. The traditional Friis Propagation Law describes the received power (PRX) in terms of transmit power (PTX), and the transmit and receive antenna gains (GTX and GRX, respectively). Friis Law assumes far-field propagation, with a range typically many wavelengths apart. In the near-field region, signal strength varies much more rapidly than for far field propagation. There are actually two different link equations – one between “like” antennas (electric-electric or magnetic-magnetic) and one between “unlike” antennas (magnetic-electric or electric-magnetic) [18]. In terms of the wave number (k = 2π⁄λ), the transmit power (PTX), the like antenna received power is:

and the unlike antenna received power is:

Near-field signals roll-off much more quickly than the more familiar far field signals. Signals between like antennas (electric to electric or magnetic to magnetic) roll off at 60 dB per decade. Signals between unlike antennas (electric to magnetic or vice versa) roll off at 40 dB per decade. By comparison, far-field signals roll-off at 20dB per decade in free space. These near-field channel relations are provided in Figure 6. Some interesting physics comes into play in the near field with respect to antenna gain and phase behavior.

Figure 6: Near-field channels diverge from far-field behavior within about a half wavelength. The divergence is particularly pronounced with the radiansphere (r = λ/2π) [After Ref. 18].

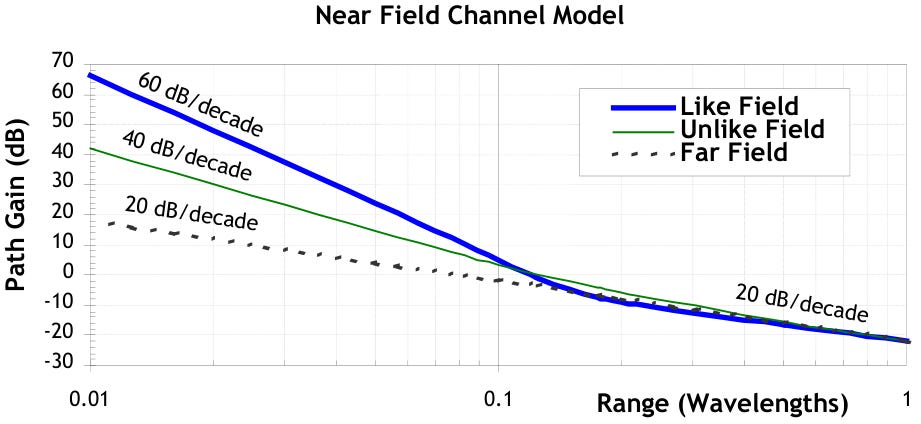
Figure 6 indicates that under some circumstances path gain may be greater than 0 dB. This means that the receive power could theoretically be greater than the transmit power. Since conservation of energy must apply to RF links, this means that antenna gain cannot be arbitrarily large. There necessarily exists a limit to antenna gain as a function of antenna size.

4.1 Gain Versus Size for Electrically Small Antennas

Our approach borrows on the concept of an antenna “boundary sphere” introduced by Wheeler [19] and extended upon by Chu [20]. A boundary sphere is the smallest sphere within which an antenna may be enclosed. Thus the radius of the boundary sphere defines the characteristic size of an antenna. A matched pair of antennas with boundary spheres of radius R may be no closer than d = 2 R without overlapping, as shown in Figure 7.

Figure 7: A matched pair of antennas with boundary spheres of radius R can be no closer than about d = 2 R without their boundary spheres overlapping [Ref. 18].

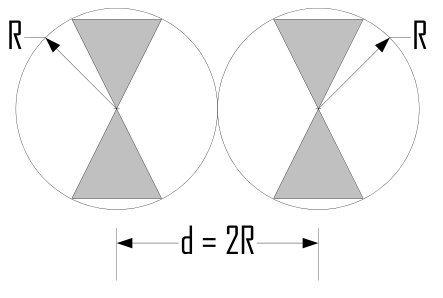
Taking this as the limit, we can apply the near-field propagation equation for like antennas (Eq. 1) to establish a limit for antenna gain versus size:

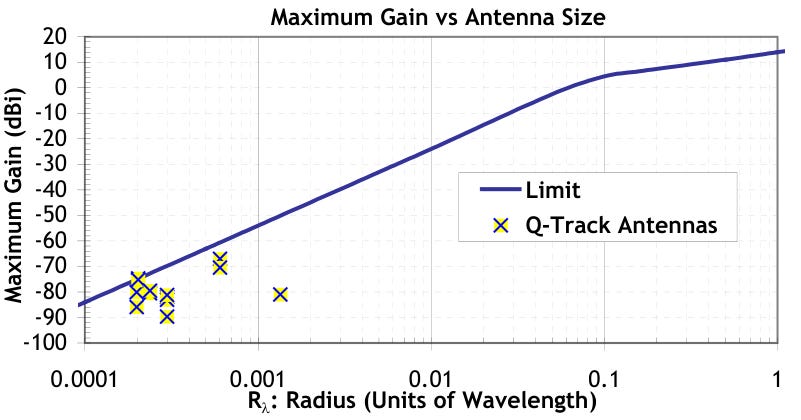
We measured gain of a variety of antennas by comparing the received power of the antenna under test to the received power of a calibrated antenna (an EMCO 6509 loop). Figure 8 presents the results. [This only works in the limit of weakly-coupled antennas, however].

Figure 8: Conservation of energy applied to the near-field link equations yields a fundamental law for maximum antenna gain versus size. Q-Track’s transmit antennas come close to the theoretical ideal for their size [© 2006; Q-Track Corporation].

4.2 Near Field Phase Relations

RF engineers and scientists often think of radio signals as a wave propagating inexorably away from a transmit antenna. An electromagnetic wave is not a single wave, however. Rather, an electromagnetic wave is a superposition of an electric wave and a magnetic wave. In the far field, many wavelengths away from a transmit antenna, this distinction is not terribly important, because the electric and magnetic waves move in lock step with perfectly synchronized phase. In the near field, within about a half wavelength or so from an electrically small antenna, the electric and magnetic field phases radically diverge. Close to an electrically small antenna, these fields are in phase quadrature, i.e. 90 degrees out of phase.

A simple thought experiment involving electromagnetic energy flow establishes why the fields are in quadrature close to an electrically small antenna and in phase far away. The Poynting vector (S = E × H) is the measure of the energy flux around the hypothetical small antenna. If the electric and magnetic fields are phase synchronous, then when one is positive, the other is positive and when one is negative the other is negative. In either case, the Poynting flux is always positive and there is always an outflow of energy. This is the radiation (or “real power”) case. If the electric and magnetic fields are in phase quadrature, then half the time the fields have the same sign and half the time the fields have opposite signs. Thus, half the time the Poynting vector is positive and represents outward energy flow and half the time the Poynting vector is negative and represents inward energy flow. This is the reactive (or “imaginary power”) case. Thus, fields in phase are associated with far field radiation and fields in quadrature are associated with near-field quadrature. As this paper will describe in detail, there is a gradual transition from near-field phase quadrature to far field phase synchronicity.

Figure 9a (left): The phase relations for an electrically small antenna were first discovered by Hertz [Ref. 21]. Figure 9b (right): Q-Track’s NFER technology takes advantage of the relative phase shift between electric and magnetic components of near-field signals. These fields are in phase quadrature (90° out of phase) close to an antenna and converge to be in phase far from an antenna.

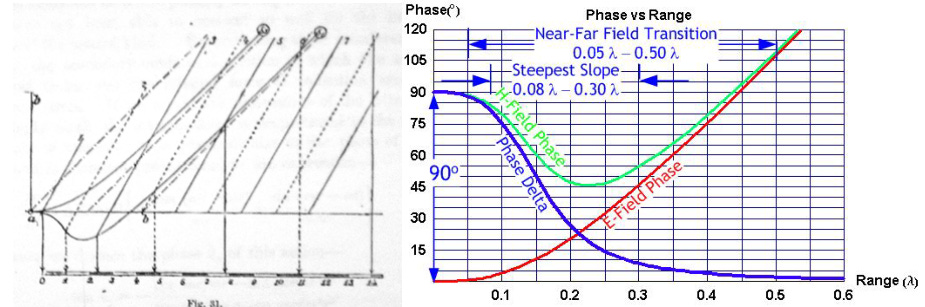
The phase relationships around small antennas were discovered by Heinrich Hertz in the 1880’s (see Figure 9) [21]. These phase relationships are the basis of a novel wireless tracking system pioneered by Q-Track using Near-Field Electromagnetic Ranging (or NFER) technology [22].

The difference in phase angle (in units of degrees) between the electric and magnetic components of a radio wave is described by [23]:

Repeated trials of a prototype transmitter and receiver in open field testing yielded results in close agreement with theoretical predictions. The prototype hardware operated at a frequency of 1295kHz where λ = 231.5m.

Figure 10 Experimental results for phase delta acquired using prototype near-field ranging hardware [Q-Track, ©2004].

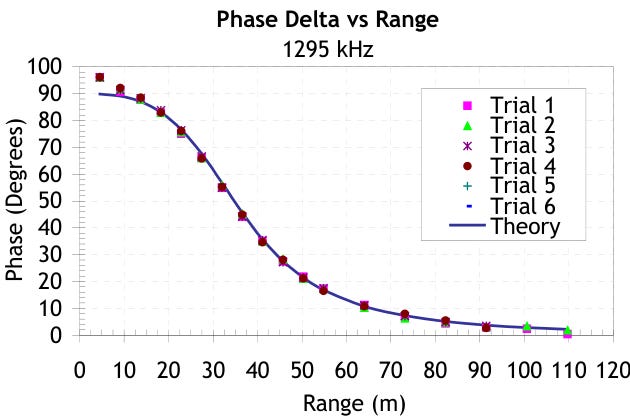
Figure 10 overlays six experimental trials with the theoretical prediction. The theoretical prediction breaks down within about 3 m where the antenna dimensions become a significant fraction of the range. In this limit, the small antenna approximation underlying the theoretical phase behavior is no longer valid.

5. Conclusions

This paper provides a brief overview of near-field RF technology with special reference to antennas and propagation. Long regarded as a technical backwater, interest in low frequencies for such applications as NFC, RFID, and RTLS are driving a renaissance in near-field RF.

Derivation of the near-field link equations and an understanding of near-field phase relations provide a foundation for understanding the behavior of antennas and propagation in the near-field context, but there is much more work waiting to be done.

Acknowledgements:

This work was supported in part by the NSF under grant OII-0539073.

Afterword (2024):

RFID and NFC have continued their growth since 2006. NFC did not find much traction in the wireless headset market contrary to my expectations, however. FreeLinc acquired Aura Communications in 2007. They market wireless headsets for police and tactical customers. See: https://www.freelinc.com/. The broader commercial market for wireless headsets is largely dominated now by Bluetooth - a more traditional 2.4 GHz wireless technology. NFC has found a sizeable niche in contactless wireless payments and other short-range secure links.

I was a co-founder of Q-Track and a co-inventor of Q-Track’s NFER location systems. NFER real-time location was a technical success, delivering highly accurate non-line-of-sight tracking. For instance, at one point about a third of U.S. nuclear plants used Q-Track’s RTLS-based Dosimulation™ systems for radiation worker training. The company failed to achieve a sizeable commercial presence, however. Q-Track was acquired by GaN Corporation in 2019, and GaN Corporation discontinued the NFER RTLS product line.

As noted, the antenna limit I derived is only valid in the weakly-coupled limit.

I contributed to another more thorough paper on how near-field link work in 2013.

References:

[1] Charles Capps, “Near-field or Far Field,” EDN, August 16, 2001, pp. 95-102.

[2] Harold H. Wheeler, “The Radiansphere Around a Small Antenna,” Proceedings of the IRE, Vol. 47, August 1959, pp. 1325-1331.

[3] William Smith, “Car Telegraph,” U.S. Patent 247,127, September 13, 1881. L.J. Phelps is sometimes credited with the first practical induction telegraph but his patent (U.S. Patent 307,984) appears to work on the principle of direct conduction with a sliding contact.

[4] Granville T. Woods, “Induction telegraph system,” U.S. Patent 373,915, November 29, 1887.

[5] Frederick Emmons Terman, Radio Engineering, New York: McGraw-Hill, 1932, p. 494.

[6] Harry Stockman, “Communication by Means of Reflected Power,” Proceedings of the IRE, October 1948, pp. 1196-1204.

[7] See http://www.auracomm.com/ for additional information. [Dead link. FreeLinc acquired Aura Communications in 2007. See https://www.freelinc.com/.]

[8] See http://www.nfc-forum.org/for more details.

[9] http://www.ecma-international.org/news/Ecma-340-NFCIP-1.htm.

[10] See http://www.checkpointsystems.com/default.aspx?page=eas for additional information.

[11] See http://www.sensormatic.com/ for additional information.

[12] Mario Cardullo, et al, “Transponder apparatus and system,” U.S. Patent 3,713,148, January 23, 1973.

[13] Jeremy Landt and Barbara Catlin, “Shrouds of Time: The History of RFID,” AIM, Inc., October 2001. See: https://transcore.com/wp-content/uploads/2017/01/History-of-RFID-White-Paper.pdf

[14] Jeff St. John, Tracking a Revolution, TriCity Herald, May 29, 2005.

[15] Wikipedia article - RFID.

[16] See http://www.q-track.com/ for more on NFER™ technology. Full disclosure – Dr. Schantz is Chief Scientist of the Q-Track Corporation.

[17] See, for instance, the excellent, but non-mathematical work of J.A. Goulbourne, HF Antenna Cookbook, Texas Instruments. See: https://www.ti.com/lit/an/scba033/scba033.pdf

[18] Hans Schantz, “A Near-field Propagation Law and a Novel Fundamental Limit to Antenna Gain versus Size,” Proceedings of the IEEE APS Conference, Washington, D.C., July 2005. Some of the discussion of the present paper was excerpted from this reference.

[19] Harold A. Wheeler, “Fundamental Limitations of Small Antennas,” Proc. IRE, 35, 1947, pp. 1479-1484.

[20] L.J. Chu, “Physical Limitations of Omni-Directional Antennas,” Journal of Applied Physics, 19, December 1948, pp. 1163-1175.

[21] Heinrich Hertz, Electric Waves, London: Macmillan and Company, 1893, p. 152.

[22] Hans Schantz and Robert DePierre, “System and Method for Near Field Electromagnetic Ranging,” U.S. Patent 6,963,301, November 8, 2005.

[23] Hans Schantz, “Near Field Phase Relationships,” Proceedings of the IEEE APS Conference, Washington, DC, July 2005. The discussion of this section is excerpted in part from this paper.