The Discovery of Neptune

A Guest Post by Oliver Lodge

We are one paid subscriber away from giving away a second copy of The Art and Science of Ultrawideband Antennas. Upgrade today, and join the eleven paid subscribers who have commented here for a chance to win.

Excerpted from Oliver Lodge, Pioneers of Science, London: Macmillan and Co. 1893, Lecture XV, pp. 317-330. Lodge presents the conventionally accepted story of the “co-discovery” of Neptune by Le Verrier and Adams. More recently, long withheld correspondence shed new light on the story. Read “NO AO-DIO Preservation Project Succeeds Long-Hidden RGO File on 1846 Planet-Chase: Safe At Last Adams’ Final Prediction Missed by Over Ten Degrees Britain’s “Discoverer”: Perfect Simp or Conniving Babe?” for a modern and more accurate take on the behind-the-scenes skullduggery and the attempted cover-up.

We approach to-night perhaps the greatest, certainly the most conspicuous, triumphs of the theory of gravitation. The explanation by Newton of the observed facts of the motion of the moon, the way he accounted for precession and nutation and for the tides, the way in which Laplace explained every detail of the planetary motions — these achievements may seem to the professional astronomer equally, if not more, striking and wonderful ; but of the facts to be explained in these cases the general public are necessarily more or less ignorant, and so no beauty or thoroughness of treatment appeals to them, nor can excite their imaginations. But to predict in the solitude of the study, with no weapons other than pen, ink, and paper, an unknown and enormously distant world, to calculate its orbit when as yet it had never been seen, and to be able to say to a practical astronomer, " Point your telescope in such a direction at such a time, and you will see a new planet hitherto unknown to man " — this must always appeal to the imagination with dramatic intensity, and must awaken some interest in almost the dullest.

The eclipse of 28 May 585 BC, courtesy Wikipedia.

Prediction is no novelty in science ; and in astronomy least of all is it a novelty. Thousands of years ago, Thales, and others whose very names we have forgotten, could predict eclipses with some certainty, though with only rough accuracy. And many other phenomena were capable of prediction by accumulated experience. We have seen, for instance (coming to later times), how a gap between Mars and Jupiter caused a missing planet to be suspected and looked for, and to be found in a hundred pieces. We have seen, also, how the abnormal proper-motion of Sirius suggested to Bessel the existence of an unseen companion. And these last instances seem to approach very near the same class of prediction as that of the discovery of Neptune. Wherein, then, lies the difference ? How comes it that some classes of prediction — such as that if you put your finger in fire it will get burnt — are childishly easy and commonplace, while others excite in the keenest intellects the highest feelings of admiration ? Mainly, the difference lies, first, in the grounds on which the prediction is based ; second, on the difficulty of the investigation whereby it is accomplished ; third, in the completeness and the accuracy with which it can be verified. In all these points, the discovery of Neptune stands out pre-eminently among the verified predictions of science, and the circumstances surrounding it are of singular interest.

William Herschel (1738-1822), courtesy, Infogalactic.

In 1781, Sir William Herschel discovered the planet Uranus. Now you know that three distinct observations suffice to determine the orbit of a planet completely, and that it is well to have the three observations as far apart as possible so as to minimize the effects of minute but necessary errors of observation. Directly Uranus was found, therefore, old records of stellar observations were ransacked, with the object of discovering whether it had ever been unwittingly seen before. If seen, it had been thought of course to be a star (for it shines like a star of the sixth magnitude, and can therefore be just seen without a telescope if one knows precisely where to look for it, and if one has good sight), but if it had been seen and catalogued as a star it would have moved from its place, and the catalogue would by that entry be wrong. The thing to detect, therefore, was errors in the catalogues : to examine all entries, and see if the stars entered actually existed, or were any of them missing. If a wrong entry were discovered, it might of course have been due to some clerical error, though that is hardly probable considering the care taken over these things, or it might have been some tailless comet or other, or it might have been the newly found planet.

John Flamsteed (1646-1719), courtesy, Infogalactic.

So the next thing was to calculate backwards, and see if by any possibility the planet could have been in that place at that time. Examined in this way the tabulated observations of Flamsteed showed that he had unwittingly observed Uranus five distinct times, the first time in 1690, nearly a century before Herschel discovered its true nature. But more remarkable still, Le Monnier, of Paris, had observed it eight times in one month, cataloguing it each time as a different star. If only he had reduced and compared his observations, he would have anticipated Herschel by twelve years. As it was, he missed it altogether. It was seen once by Bradley also. Altogether it had been seen twenty times.

Pierre Charles Le Monnier (1715-1799), courtesy, Infogalactic.

These old observations of Flamsteed and those of Le Monnier, combined with those made after Herschel's discovery, were very useful in determining an exact orbit for the new planet, and its motion was considered thoroughly known. It was not an exact ellipse, of course : none of the planets describe exact ellipses — each perturbs all the rest, and these small perturbations must be taken into account, those of Jupiter and Saturn being by far the most important.

For a time Uranus seemed to travel regularly and as expected, in the orbit which had been calculated for it ; but early in the present century it began to be slightly refractory, and by 1820 its actual place showed quite a distinct discrepancy from its position as calculated with the aid of the old observations. It was at first thought that this discrepancy must be due to inaccuracies in the older observations, and they were accordingly rejected, and tables prepared for the planet based on the newer and more accurate observations only. But by 1830 it became apparent that it would not accurately obey even these. The error amounted to some 20". By 1840 it was as much as 90” , or a minute and a half [NOTE: the angular diameter of the moon is 0.52 degrees, or 31.2’, or 1872”. This discrepancy is quite distinct, but still it is very small, and had two objects been in the heavens at once, the actual Uranus and the theoretical Uranus, no unaided eye could possibly have distinguished them or detected that they were other than a single star.

Perturbations of Uranus. The chance observations by Flamsteed, by Le Monnier, and others, are plotted in this diagram, as well as the modern determinations made after Herschel had discovered the nature of the planet. The decades are laid off horizontally. Vertical distance represents the difference between observed and subsequently calculated longitudes— in other woi'ds, the principal perturbations caused by Neptune. To show the scale, a number of standard things are represented too by lengths measured upwards from the line of time, viz : the smallest quantity perceptible to the naked eye, — the maximum angle of aberration, of nutation, and of stellar parallax ; though this last is too small to be properly indicated. The perturbations are much bigger than these ; but compared with what can be seen without a telescope they are small — the distance between the component pairs of e Lyrge (210") (see fig. 86, page 2SS), which a few keen-eyed persons can see as a simple double star, being about twice the greatest perturbation.

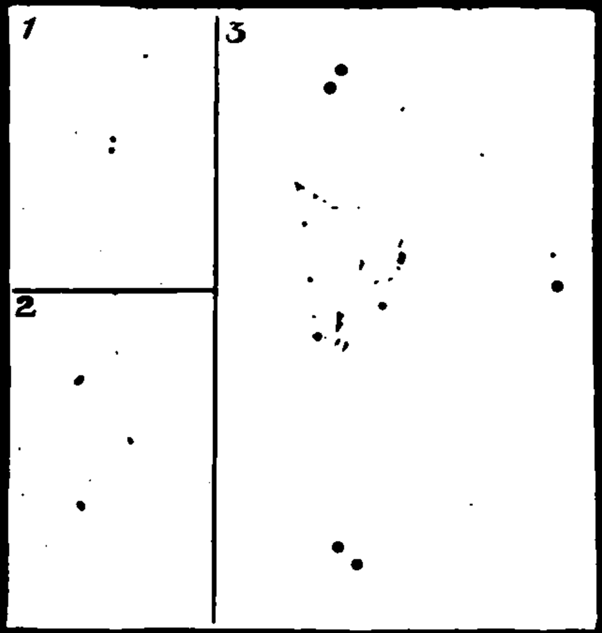
The chance observations by Flamsteed, by Le Monnier, and others, are plotted in this diagram, as well as the modern determinations made after Herschel had discovered the nature of the planet. The decades are laid off horizontally. Vertical distance represents the difference between observed and subsequently calculated longitudes— in other words, the principal perturbations caused by Neptune. To show the scale, a number of standard things are represented too by lengths measured upwards from the line of time, viz : the smallest quantity perceptible to the naked eye, — the maximum angle of aberration, of nutation, and of stellar parallax ; though this last is too small to be properly indicated. The perturbations are much bigger than these ; but compared with what can be seen without a telescope they are small — the distance between the component pairs of e Lyrge (210"), which a few keen-eyed persons can see as a simple double star, being about twice the greatest perturbation.

The double-double star e Lyra; as seen under three different powers.

The diagram shows all the irregularities plotted in the light of our present knowledge ; and, to compare with their amounts, a few standard things are placed on the same scale, such as the smallest interval capable of being detected with the unaided eye, the distance of the component stars in € Lyrae, the constants of aberration, of nutation, and of stellar parallax.

The errors of Uranus therefore, though small, were enormously greater than things which had certainly been observed ; there was an unmistakable discrepancy between theory and observation. Some cause was evidently at work on this distant planet, causing it to disagree with its motion as calculated according to the law of gravitation. Some thought that the exact law of gravitation did not apply to so distant a body. Others surmised the presence of some foreign and unknown body, some comet, or some still more distant planet perhaps, whose gravitative attraction for Uranus was the cause of the whole difficulty — some perturbations, in fact, which had not been taken into account because of our ignorance of the existence of the body which caused them.

But though such an idea was mentioned among astronomers, it was not regarded with any special favour, and was considered merely as one among a number of hypotheses which could be suggested as fairly probable.

It is perfectly right not to attach much importance to unelaborated guesses. Not until the consequences of an hypothesis have been laboriously worked out — not until it can be shown capable of producing the effect quantitatively as well as qualitatively — does its statement rise above the level of a guess, and attain the dignity of a theory. A later stage still occurs when the theory has been actually and completely verified by agreement with observation.

Now the errors in the motion of Uranus, i.e. the discrepancy between its observed and calculated longitudes— all known disturbing causes, such as Jupiter and Saturn, being allowed for — are as follows (as quoted by Dr. Haughton) in seconds of arc : —

These are the numbers plotted in the above diagram, where H marks the discovery of the planet and the beginning of its regular observation.

Something was evidently the matter with the planet. If the law of gravitation held exactly at so great a distance from the sun, there must be some perturbing force acting on it besides all those known ones which had been fully taken into account. Could it be an outer planet ? The question occurred to several, and one or two tried if they could solve the problem, but were soon stopped by the tremendous difficulties of calculation.

The ordinary problem of perturbation is difficult enough : Given a disturbing planet in such and such a position, to find the perturbations it produces. This problem it was that Laplace worked out in the Mecanique Celeste.

But the inverse problem : Given the perturbations, to find the planet which causes them — such a problem had never yet been attacked, and by only a few had its possibility been conceived. Bessel made preparations for trying what he could do at it in 1840, but he was prevented by fatal illness.

John Couch Adams (1819 - 1892), courtesy, Infogalactic.

In 1841 the difficulties of the problem presented by these residual perturbations of Uranus excited the imagination of a young student, an undergraduate of St. John's College, Cambridge — John Couch Adams by name — and he determined to have a try at it as soon as he was through his Tripos. In January, 1843, he graduated as Senior Wrangler, and shortly afterwards he set to work. In less than two years he reached a definite conclusion ; and in October, 1845, he wrote to the Astronomer-Boyal, at Greenwich, Professor Airy, saying that the perturbations of Uranus would be explained by assuming the existence of an outer planet, which he reckoned was now situated in a specified latitude and longitude.

George Biddell Airy, English mathematician and astronomer (1801 – 1892), courtesy Infogalactic.

We know now that had the Astronomer-Royal put sufficient faith in this result to point his big telescope to the spot indicated and commence sweeping for a planet, he would have detected it within 1 J° of the place assigned to it by Mr. Adams. But any one in the position of the AstronomerEoyal knows that almost every post brings an absurd letter from some ambitious correspondent or other, some of them having just discovered perpetual motion, or squared the circle, or proved the earth flat, or discovered the constitution of the moon, or of ether, or of electricity ; and out of this mass of rubbish it requires great skill and patience to detect such gems of value as there may be.

Now this letter of Mr. Adams's was indeed a jewel of the first water, and no doubt bore on its face a very different appearance from the chaff of which I have spoken ; but still Mr. Adams was an unknown man : he had graduated as Senior Wrangler it is true, but somebody must graduate as Senior Wrangler every year, and every year by no means produces a first-rate mathematician. Those behind the scenes, as Professor Airy of course was, having been a Senior Wrangler himself, knew perfectly well that the labelling of a young man on taking his degree is much more worthless as a testimony to his genius and ability than the general public are apt to suppose.

Was it likely that a young and unknown man should have successfully solved so extremely difficult a problem ? It was altogether unlikely. Still, he would test him : he would ask for further explanations concerning some of the perturbations which he himself had specially noticed, and see if Mr. Adams could explain these also by his hypothesis. If he could, there might be something in his theory. If he failed — well, there was an end of it. The questions were not difficult. They concerned the error of the radius vector. Mr. ,Adams could have answered them with perfect case ; but sad to say, though a brilliant mathematician, he was not a man of business. He did not answer Professor Airy's letter.

The great equatorial telescope in the Dome at Greenwich., courtesy, Wikipedia.

It may to many seem a pity that the Greenwich Equatoreal was not pointed to the place, just to see whether any foreign object did happen to be in that neighbourhood ; but it is no light matter to derange the work of an Observatory, and alter the work mapped out for the staff into a sudden sweep for a new planet, on the strength of a mathematical investigation just received by post. If observatories were conducted on these unsystematic and spasmodic principles, they would not be the calm, accurate, satisfactory places they are.

Of course, if any one could have known that a new planet was to be had for the looking, any course would have been justified ; but no one could know this. I do not suppose that Mr. Adams himself could feel all that confidence in his attempted prediction. So there the matter dropped. Mr. Adams's communication was pigeon-holed, and remained in seclusion for eight or nine months.

Meanwhile, and quite independently, something of the same sort was going on in France. A brilliant young mathematician, born in Normandy in 1811, had accepted the post of Astronomical Professor at the Ecole Polytechnique, then recently founded by Napoleon. His first published papers directed attention to his wonderful powers ; and the official head of astronomy in France, the famous Arago, suggested to him the unexplained perturbations of Uranus as a worthy object for his fresh and well-armed vigour.

Urbain Jean Joseph Le Verrier (1811 - 1877), French astronomer and mathematician, courtesy, Infogalactic.

At once he set to work in a thorough and systematic way. He first considered whether the discrepancies could be due to errors in the tables or errors in the old observations. He discussed them with minute care, and came to the conclusion that they were not thus to be explained away. This part of the work he published in November, 1845.

He then set to work to consider the perturbations produced by Jupiter and Saturn, to see if they had been with perfect accuracy allowed for, or whether some minute improvements could be made sufficient to destroy the irregularities. He introduced several fresh terms into these perturbations, but none of them of sufficient magnitude to do more than slightly lessen the unexplained perturbations.

He next examined the various hypotheses that had been suggested to account for them : — Was it a failure in the law of gravitation? Was it due to the presence of a resisting medium ? Was it due to some unseen but large satellite ? Or was it due to a collision with some comet ?

All these he examined and dismissed for various reasons one after the other. It was due to some steady continuous cause — for instance, some unknown planet. Could this planet be inside the orbit of Uranus? No, for then it would perturb Saturn and Jupiter also, and they were not perturbed by it. It must, therefore, be some planet outside the orbit of Uranus, and in all probability, according to Bode's empirical law, at nearly double the distance from the sun that Uranus is. Lastly he proceeded to examine where this planet was, and what its orbit must be to produce the observed disturbances.

Uranus's and Neptune's relative positions. The above diagram, drawn to scale by Dr. Haugliton, shows the paths of Uranns and Neptune, and their positions from 17S1 to 1840, and illustrates the direction of their mutual perturbing force. In 1822 the planets were in conjunction, and the force would then perturb the radius vector (or distance from the sun), but not the longitude (or place in orbit). Before that date Uranus had been hurried along, and after that date it had been retarded, by the pull of Neptune, and thus the observed discrepancies from its computed place were produced. The problem was first to disentangle the outstanding perturbations from those which would be caused by Jupiter and Saturn and all other known causes, and then to assign the place of an outer planet able to produce precisely those perturbations in Uranus.

Not without failures and disheartening complications was this part of the process completed. This was, after all, the real tug of war. So many unknown quantities : its mass, its distance, its excentricity, the obliquity of its orbit, its position at any time — nothing known, in fact, about the planet except the microscopic disturbance it caused in Uranus, some thousand million miles away from it.

Without going into further detail, suffice it to say that in June, 1846, he published his last paper, and in it announced to the world his theoretical position for the planet.

Professor Airy received a copy of this paper before the end of the month, and was astonished to find that Leverrier's theoretical place for the planet was within 1° of the place Mr. Adams had assigned to it eight months before. So striking a coincidence seemed sufficient to justify a Herschelian "sweep" for a week or two.

But a sweep for so distant a planet would be no easy matter. When seen in a large telescope it would still only look like a star, and it would require considerable labour and watching to sift it out from the other stars surrounding it. We know that Uranus had been seen twenty times, and thought to be a star, before its true nature was by Herschel discovered ; and Uranus is only about half as far away as Neptune is.

Neither in Paris nor yet at Greenwich was any optical search undertaken ; but Professor Airy wrote to ask M. Leverrier the same old question as he had fruitlessly put to Mr. Adams : Did the new theory explain the errors of the radius vector or not ? The reply of Leverrier was both prompt and satisfactory — these errors were explained, as well as all the others. The existence of the object was then for the first time officially believed in.

The British Association met that year at Southampton, and Sir John Herschel was one of its Sectional Presidents. In his inaugural address, on September 10th, 1846, he called attention to the researches of Leverrier and Adams in these memorable words :

The past year has given to us the new [minor] planet Astraea ; it has done more — it has given us the probable prospect of another. We see it as Columbus saw America from the shores of Spain. Its movements have been felt trembling along the far-reaching line of our analysis with a certainty hardly inferior to ocular demonstration.

It was about time to begin to look for it. So the Astronomer-Royal thought on reading Leverrier's paper. But as the national telescope at Greenwich was otherwise occupied, he wrote to Professor Challis, at Cambridge, to know if he would permit a search to be made for it with the Northumberland Equatoreal, the large telescope of Cambridge University, presented to it by one of the Dukes of Northumberland .

James Challis (1803 – 1882), English clergyman, physicist and astronomer, .courtesy, Wikipedia.

Professor Challis said he would conduct the search himself ; and shortly commenced a leisurely and dignified series of sweeps round about the place assigned by theory, cataloguing all the stars which he observed, intending afterwards to sort out his observations, compare one with another, and find out whether any one star had changed its position ; because if it had it must be the planet. He thus, without giving an excessive time to the business, accumulated a host of observations, which he intended afterwards to reduce and sift at his leisure.

The wretched man thus actually saw the planet twice — on August 4th and August 12th, 1846— without knowing it. If only he had had a map of the heavens containing telescopic stars down to the tenth magnitude, and if he had compared his observations with this map as they were made, the process would have been easy, and the discovery quick. But he had no such map. Nevertheless one was in existence : it had just been completed in that country of enlightened method and industry — Germany. Dr. Bremiker had not, indeed, completed his great work — a chart of the whole zodiac down to stars of the tenth magnitude — but portions of it were completed, and the special region where the new planet was expected happened to be among the portions already just done. But in England this was not known.

Meanwhile, Mr. Adams wrote to the Astronomer-Royal several additional communications, making improvements in his theory, and giving what he considered nearer and nearer approximations for the place of the planet. He also now answered quite satisfactorily, but too late, the question about the radius vector sent to him months before.

Let us return to Leverrier. This great man was likewise engaged in improving his theory and in considering how best the optical search could be conducted. Actuated, probably, by the knowledge that in such matters as cataloguing and mapping Germany was then, as now, far ahead of all the other nations of the world, he wrote in September (the same September as Sir John Herschel delivered his eloquent address at Southampton) to Berlin. Leverrier wrote, I say, to Dr. Galle, head of the Observatory at Berlin, saying to him, clearly and decidedly, that the new planet was now in or close to such and such a position, and that if he would point his telescope to that part of the heavens he would see it ; and, moreover, that he would be able to tell it from a star by its having a sensible magnitude, or disk, instead of being a mere point.

German astronomer Johann Gottfried Galle (1812 – 1910), courtesy, Infogalactic.

Galle got the letter on the 23rd of September, 1846. That same evening he did point his telescope to the place Leverrier told him, and he saw the planet that very night. He recognized it first by its appearance. To his practised eye it did seem to have a small disk, and not quite the same aspect as an ordinary star.

The 9" refractor which was used to discover Neptune is at Deutsches Museum in Munich today, courtesy, Wikipedia.

He then consulted Bremiker's great star chart, the part just engraved and finished, and sure enough on that chart there was no such star there. Undoubtedly it was the planet.

Excerpt from the Hora XXI sky chart of the Berlin Science Academy completed by Carl Bremiker. The predicted location (square) and the observed location (circle) were noted in pencil, allegedly by Galle, but at some time after the discovery, courtesy, Wikipedia.

The news flashed over Europe at the maximum speed with which news could travel at that date (which was not very fast) ; and by the 1st of October Professor Challis and Mr. Adams heard it at Cambridge, and had the pleasure of knowing that they were forestalled, and that England was out of the race.

Galle discovered Neptune in the location Le Verrier predicted on September 23, 1845, courtesy, Infogalactic.

It was an unconscious race to all concerned, however. Those in France knew nothing of the search going on in England. Mr. Adams's papers had never been published ; and very annoyed the French were when a claim was set up on his behalf to a share in this magnificent discovery. Controversies and recriminations, excuses and justifications, followed ; but the discussion has now settled down. All the world honours the bright genius and mathematical skill of Mr. Adams, and recognizes that he first solved the problem by calculation. All the world, too, perceives clearly the no less eminent mathematical talents of M. Leverrier, but it recognizes in him something more than the mere mathematician — the man of energy, decision, and character.

Enjoyed the article, but maybe not quite enough to spring for a paid subscription?
Then click on the button below to buy me a coffee. Thanks!

Follow Online:

You may follow me online in other places as well:

• Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞

• Gab: @aetherczar

• Twitter: @aetherczar

• Amazon: Hans G. Schantz

• Wise of Heart Substack

• ResearchGate

• Google Scholar

• ORCID