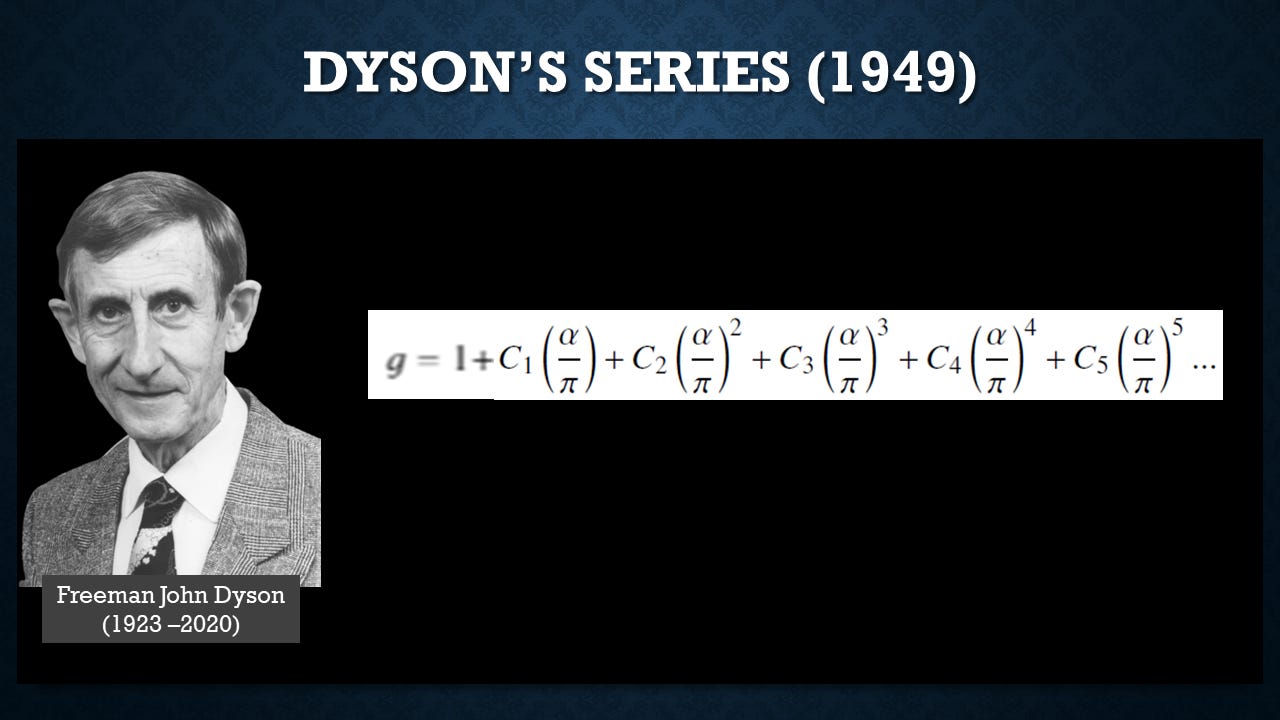While I continue working on getting Fields & Energy Book I: Fuindamentals & Origins of Electromagnetism finalized and copies on order, here’s a talk I gave a couple of years ago at the LibertyCon. As usual, the transcript retains a great many verbal quirks, but will allow you to follow the argument without watching the video, if you prefer.
Transcript: What Physicists Don't Know About Electromagnetism
Okay. I have last year’s talk on YouTube, but unfortunately my sound didn't work, and I had to rely on the camera sound. It's a little bit iffy. But if you want to learn about how electromagnetism, or what can electromagnetism tell us about quantum mechanics, that was last year's talk, and there's a little bit of overlap in the talk here.
Well, it's 3 o'clock, so let me get started. My talk is on the subject, “What Physicists Don't Know About Electromagnetism.”
Now, I am a physicist by training, but I've spent most of my career doing things in applied electromagnetics, designing ultra-wideband antennas, designing near-field systems and near-field links and electrically small antennas and so forth. But I've always wondered how electromagnetism works. And I think there are a lot of very fascinating aspects of classical electromagnetism that have been overlooked by physics that offer some answers to some of the outstanding problems in physics today.
A Tale of Two Books
So let's get started. To begin with, I want to start with a tale of two books. The book you see there on the left, that's Electromagnetic Theory by Stratton, published in 1941. That is the book that physicists and engineers alike used on the Manhattan Project. They used developing radar. This was the book everyone used to study electromagnetic theory, physicists and engineering alike in 1941.
And you can see a whole host of really practical, you know, applied electromagnetic topics are covered in that book. On the right is Jackson's classical electrodynamics. Now, that's the second edition that I used when I was in grad school. But even the third edition, you know, doesn't change the topic selection all that much.
And you'll notice of the topics covered in Stratton, a lot of the really important topics are no longer covered in Jackson. Things like over-the-earth propagation, surface waves, Norton Sommerfeld ground conditions, most of the most practical kinds of wave guides, the principle of electromagnetic similitude and scaling, that's how you change electromagnetic properties to make a model that's bigger or smaller to operate at different frequencies. And about half of the practical, in fact, the more practical aspects of radiation theory, Jackson just covers some of the basics, dipoles and center-fed linear antennas, nothing on arrays, nothing on phase coherent superposition from different elements and so forth.
So arguably, Today's physicists who are educated using the curriculum out of Jackson are less informed about practical electromagnetics than their counterparts of 80 years ago. How could this happen?
Thesis & Introduction
Well, what have physicists been doing in electromagnetics since World War II? Well, the short answer is quantum electrodynamics, the quantum theory of how light, electromagnetics, interacts with matter. Amazing accuracy, the crown jewel of physics, 12-digit agreement between theory and experiment.
Well, so because physicists have left practical electromagnetism to the engineers, All the theory's been figured out. That's an exercise for the drudges who work soldering things together to apply. There's nothing fundamental left to say about nature.
But electromagnetism, though, it turns out has advanced a little bit since the days of Stratton in ways that physicists do not appreciate. So the topic of this talk is going to be what physicists don't know about electromagnetics.
The Strange Story of QED
I'll begin by presenting the strange story of quantum electrodynamics. And as a physicist, as someone who studied the subject in grad school, getting my PhD, I had no idea how bad it was. And I really owe this guy, Oliver Consa, who wrote this article, “Something is Wrong in the State of QED,” which I'm basically summarizing here for the next 20 minutes or so. And if you want to go into more details than the kind of superficial, top-level version I'm presenting, I suggest you take a look at what he had to say.
The Monster From Shelter Island
So we begin by going to the first major conference in physics after World War II ended, the Shelter Island Conference on the foundations of quantum mechanics. All the younger generation of physicists were there. One of the key attendees, Julian Schwinger, said it was the first time that people who had all this physics pent up in them for five years could talk to each other without somebody peering over their shoulders and saying, is this cleared?
And one of the key things that everyone is interested in talking about is something called the Lamb shift. Willis Eugene Lamb discovered there was about a 1 gigahertz, 1,000 megacycle or megahertz discrepancy between the hydrogen energy levels.
Another physicist, Rabi, noted this was a 0.1% anomaly in the hyperfine structure of hydrogen, and Gregory Bright interpreted that as being due to the anomalous magnetic moment of the electron. The electron has a certain amount of angular momentum, and that rotating charge gives rise to a little bit of a magnetic moment.
But the key point here is this meant Dirac's relativistic quantum mechanics was wrong, or at least needed a little bit of correction. And the Dirac quantum mechanics, that was the then crown jewel of the physical understanding of the universe.
So it was interpreted as a perturbation due to the quantum vacuum that hadn't been accounted for in Dirac's theory. And so everyone there at Shelter Island talked about it.
On the train ride home, Hans Bethe, came up with an idea. I won't go into the details of the equation, but what he came up with was a mathematical expression for that frequency difference. It depends on this factor K here. Well, that K is an infinite series. It goes to infinity.
But he said, well, let's just assume that it stops at the rest mass of the electron. So let's solve the problem of the math going to infinity. Then he said, well, and in order to get the numbers to work out more or less correctly, this constant in the equation had to be set to a value of 242 electron volts, which, as you know, is a very big number. But by jiggering the numbers around, they were able to get, you know, Beta was able to get a calculation that was more or less giving that 1 gigahertz answer.
Well, the problem was solved by Schwinger. And he said, no, all you have to do is take a very important physical constant, the fine structure constant. And that's about six times larger than the discrepancy that we're seeing here. And 2 pi, that's about six. So if we divide that by 2 pi, we end up getting a correction that lines up pretty closely with the experimental value.
The Pocono Conference
And he wrote this in a short paper and didn't really explain the theoretical reasoning for why that popped up there. So about a year later, there was another conference, a Pocono conference, and everyone was looking forward to hearing, how did Schwinger come up with this answer?
And Schwinger spent about five or six hours just doing math on the chalkboard. He drove out the entire audience with the exception of Beta and Fermi, who were the only two left behind at the end of the five or six hours, And as Oppenheimer quipped, others gave talks to show others how to do the calculation. Schwinger gave talks to show that only he could do it.
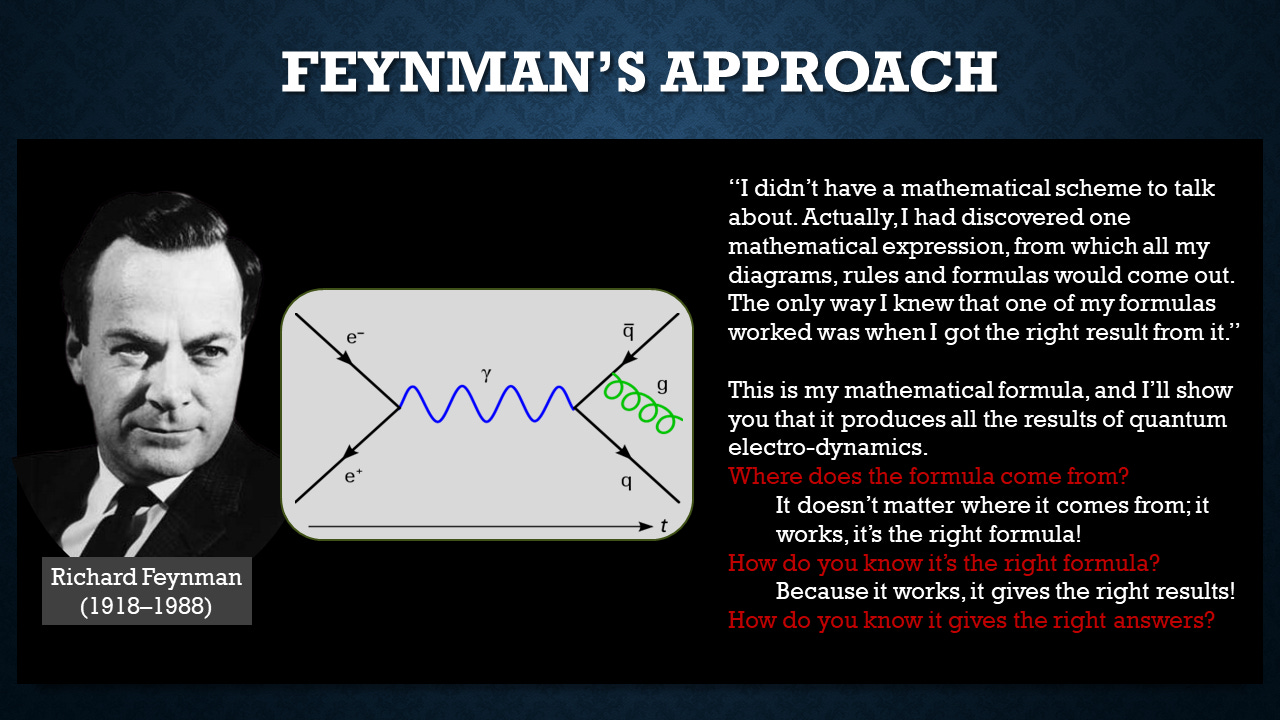
Well, the next day wasn't all that much better. This young guy named Richard Feynman came up, and he presented a bunch of crazy diagrams up on the board and was trying to align them with perturbations in the quantum vacuum. And… the red didn't show up very well in there?
He was describing what happened. He said he didn't have a mathematical scheme to talk about. The only way he knew one of his formulas worked was when he got it right. So he was asked, where does the formula come from?
His answer, it doesn't matter where it comes from. It works. It's the right formula.
And how do you know it's the right formula? Because it works. It gives the right results.
Well, how do you know that it's giving the right answers? Well, they line up with experiment.
So that was the attitude, the kind of freewheeling mathematical, not really grounded in any fundamental physical theory approach that Feynman was taking. And the attendees there did not find that very satisfying either.
Dyson’s Series
Now, about a year later, young British physicist Freeman Dyson noted and argued that you could treat the whole problem as being a perturbation theory. And this is kind of common in physics where if you have a small correction factor, you can look at a power series where you take a linear term and a square term, cube term, and so forth, just add those up in order to get the right corrections.
And he showed that effectively the Schwinger approach and the Feynman approach were equivalent. Well, Dirac's reaction was to say, “how do they manage with these incorrect equations? These equations lead to infinities when one tries to solve them. These infinities ought not to be there. They remove them artificially. Just because the results happen to be in agreement with observations does not prove that one's theory is correct.”
And I like this other comment that “I am very dissatisfied with the situation because this so-called ‘good theory’ does involve neglecting infinities which appear in its equations, ignoring them in an arbitrary way. This is just not sensible mathematics. Sensible mathematics involves disregarding a quantity when it is small, not neglecting it just because it is infinitely great and you do not want it!”
Oppenheimer, now this is Dyson talking about Oppenheimer's reaction. Oppenheimer “did not believe that the ideas of Schwinger and Feynman had much to do with reality. I had known that he had never appreciated Feynman, but it came as a shock to hear him now violently opposing Schwinger, his own student, whose work he had acclaimed so enthusiastically six months earlier. He had somehow become convinced during his stay in Europe that physics was in need of radically new ideas, that this quantum electrodynamics of Schwinger and Feynman was just another misguided attempt to patch up old ideas with fancy mathematics.”
Fermi, well, his reaction was to say “there are two ways of doing calculations in physics. One way, the way he prefers, is to have a clear physical picture of the process that you're calculating. The other way is to have a precise and self-consistent mathematical formalism. You have neither.”
When Dyson tried to counter by pointing out the agreement between the experiment and the theory, Fermi asked how many free parameters were used in order to obtain it. Four, Dyson said. Fermi remarked, “I remember my old friend Johnny von Neumann used to say with four parameters, I can fit an elephant. And with five, I can make him wiggle his trunk.”
So very soon the technique was being applied to meson problems, because that was the heavier subatomic particles in understanding how they behaved. And even Feynman was skeptical of that, because the whole idea of a series expansion works only when the parameter that you're expanding here is very, very small. If it starts to get very large, like in nuclear force attractions, it doesn't really apply at all.
And Feynman's remark was, don't believe any calculation in Meson theory that uses a Feynman diagram. Take a look at a modern nuclear physics book that's describing this, and you'll see Feynman diagrams all over the place.
Experiment and Theory Pursue Each Other
Well, let's go back to QED and this calculation of the anomalous electron moment, or the G factor. So there were some new experimental results. We had Schwinger's prediction here, which lined up beautifully with the 1947 result. But then, in 1949, Gardner and Purcell got a new, different, lower result inconsistent with the theory.
So, of course, the natural thing to do was to use the power series, calculate the next term, and see if they could get it to align. And two independent calculations by Kroll and Karplus, two associates of Feynman, independently did the calculation separately and then noted, yep, we got the same answer. And that was the answer, and they restored the agreement between QED and the experimental measurement. QED triumphs.
Well, then a little wrinkle popped up because Dyson proved that his series was inherently divergent even after you do the renormalization of math. So the whole process involves using a series that's inherently divergent. And you can cut it off arbitrarily at a certain point and get answers all over the place. But in theory, if you added up all the terms, you'd have an infinite result. So it really, the answer you get depends on where you happen to stop in summing up the terms.
Well, then there was a little bit of a wrinkle here. Because six years after Kroll and Karplus independently obtained their result, it was a new measurement that said, no, we're closer to the old measurement. So the result that they did involved summing up a large number of Feynman diagrams. I provided a little sketch there. Very complicated calculation.
And when a bunch of people redid it, they discovered, well, What they discovered is Kroll and Karplus worked together on the problem and kept working together on the problem until the answer they had mutually come up with… ended up being in alignment with the experimental theory, so that's what they reported. And, you know, Feynman kind of glossed over that, well, you know, they happened to iron out the differences between their calculations so they weren't really independent.
I mean, that's really soft peddling it. They claimed it was independent, and they lied, and they worked together on it, and they very clearly ended up with just reporting an arbitrary theoretical prediction to align with the experimental result that was back there.
And it took six years for anyone to notice that there was a problem with that calculation.
So, in 1957, Peterman and Sommerfeld both independently (and I think it really was) came up with a different calculation. You'll notice there's a little bit of a difference between minus 2.9 and minus 0.38, like a factor of 10. But that got the alignment back more or less close to the experimental result.
Well, then in 1961, we got a more accurate measurement from a Michigan team, very precise measurement. And you'll notice they had a very, very tight error bound on their answer, a very, very tight error bound on their answer that excluded the theoretical value. But they went back into their experiment and reanalyzed it and were able to figure out some other possible sources of error and reported an error bound that was much larger and large enough to include the theoretical answer.
Well, then in 1963, we had another experiment that reported almost exact agreement with the solution of 1957.
The Nobel Prize
And as a result, the Nobel Prize was awarded to the pioneers in quantum electrodynamics shared by Feynman, Schwinger, and a Japanese physicist, Shinichiro Tomonaga.
Well, then, a decade or so later, some more accurate measurements started to come out that started to call the old theoretical answer into question. And people started to calculate what that third coefficient in the series would be. But the initial calculation clearly wasn't helping and would only make matters worse.
Finally, in 1996, and this is a measure of how complicated this is, requiring computer assistants to calculate all the equations involved with each of the Feynman diagrams that are involved in calculating one of those coefficients. Finally, in 1996, there was a report of a new calculation of that C3 coefficient, and we got alignment of theory and agreement yet again.
Well, the problem is when people started going further and trying to calculate the next two agreements, or the next two coefficients, no one was able to get that to work out. They just would not align with the theoretical, with the experimental results.
So they added three new fudge factors, provided a justification for them, and once again managed to align the theoretical result with the experimental measurement.
So the result is today we have the crown jewel of physics with 12-digit agreement between theory and experiment that if you try to apply it to a muon, which is kind of a heavier cousin of the electron, it doesn't work and no one knows how to fix it.
QED: A Summary
So that's what physicists were doing in electromagnetics after World War II.
Now, to summarize, Feynman said, we found nothing wrong with the theory of quantum electrodynamics. It is therefore, I would say, the jewel of physics our proudest profession.
But in a little more candid moment, he said, the shell game that we play is technically called renormalization, but no matter how clever the word, it is still what I would call a dippy process. Having to resort to such hocus-pocus has prevented us from proving that the theory of quantum electrodynamics is mathematically self-consistent. It's surprising that the theory still hasn't been proved self-consistent one way or the other by now. I suspect that renormalization is not mathematically legitimate.
Dyson was a little more honest, and this is in 2006. He commented, as one of the inventors of QED, I remember that we thought a QED in 1949 as a temporary and jerry-built structure with mathematical inconsistencies and renormalized infinities swept under the rug. We did not expect it to last more than 10 years before something more solidly built theory would replace it. Now, 57 years have gone by, and that ramshackle structure still stands.
Progress in Applied Electromagnetism
So what was going on in applied electromagnetism? Well, one key concept is the concept of impedance. Now, this was familiar to circuit engineers. That's just the ratio of voltage to current for AC circuits, which is referred to as impedance.
Well, a Russian-American mathematician who worked for Bell Labs, Sergei Schelkunoff, noted that you could take that concept and you could apply it to fields and define a field impedance that's the ratio of the electric to the magnetic fields. It allows extending all the useful practice and techniques that we have dealing with impedance in electrical circuits and apply them to fields.
A key factor that very few people appreciate, it is an attribute of the field as well as of the medium. So, for instance, in free space, the impedance of free space is 376 ohms. So if you have an electromagnetic wave of whatever frequency, the ratio of its electric to magnetic field in free space, 376.7, et cetera, ohms.
But if that field is interacting with another field, if you have a constructive or a destructive interference where you're shifting that balance between the electric and magnetic energy, it can be anything. It could be an open. It could be a short. It's a property of the field as well as of the medium itself.
Smith Charts
And you could generalize this to a one-dimensional transmission line to understand electromagnetic field problems and analyze them kind of as easily as you would a transmission line.
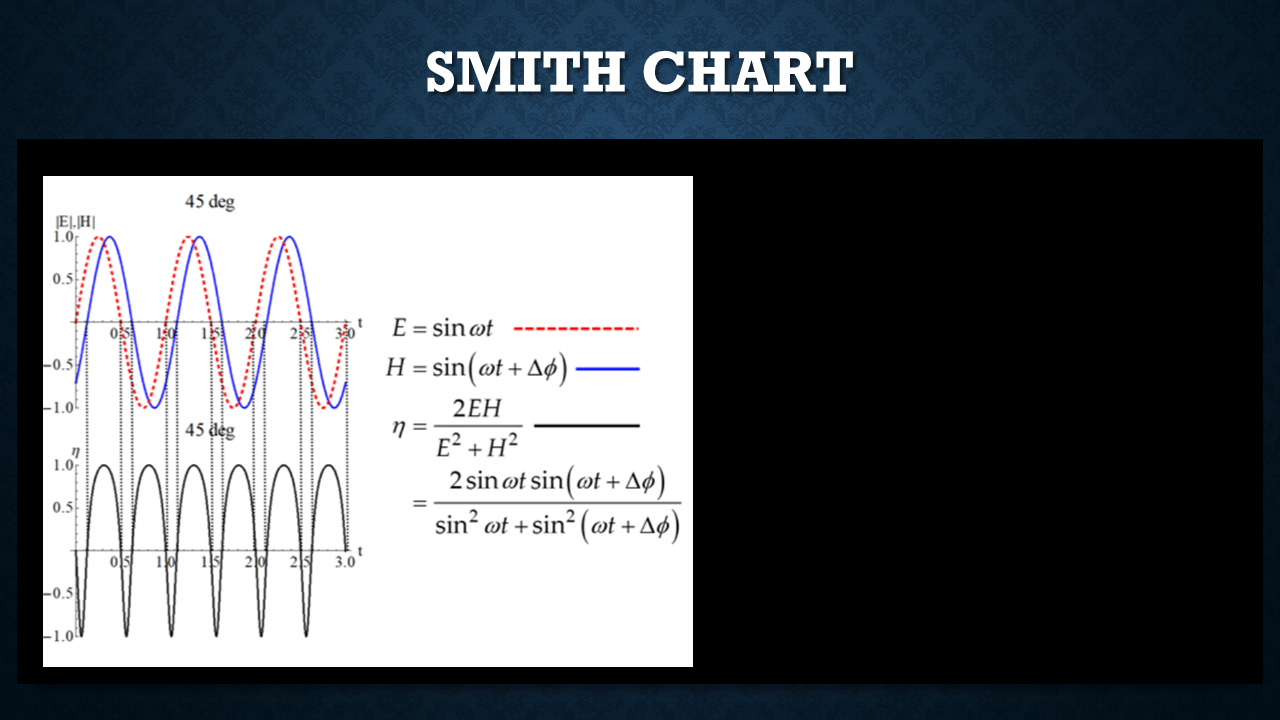
So, for instance, If you studied electrical engineering, and I think most every engineer gets a little bit of this AC theory when they're in their undergraduate career, you can take a look at a signal. Now, in this case, we're talking electric fields and magnetic fields. You probably saw it as voltages and currents. And if there's a little bit of a phase difference between them, you have the energy or power going forward and then back if they have the same sign.
So you get energy moving in this pattern down here. And you can calculate what the energy velocity is as a result of the amplitudes of those two fields. And it's really kind of interesting how if you have the two fields in quadrature, 90-degree phase difference between them, you end up with the energy just oscillating in and out, and there's no net energy flow. That's referred to as reactive energy.
And then as you start to align the phases closer and closer, you get to the point where they're exactly in phase, and all that energy is moving. It's pure real power or real energy moving down the transmission line.
Well, there's a very clever technique that a gentleman named Philip Hager Smith came up with to plot these on this very artistically, aesthetically pleasing chart called the Smith Chart. And you can take a whole undergraduate class in what this is and what this means and how to use this. So I'll summarize a little bit of the basics just to give you a flavor for it.
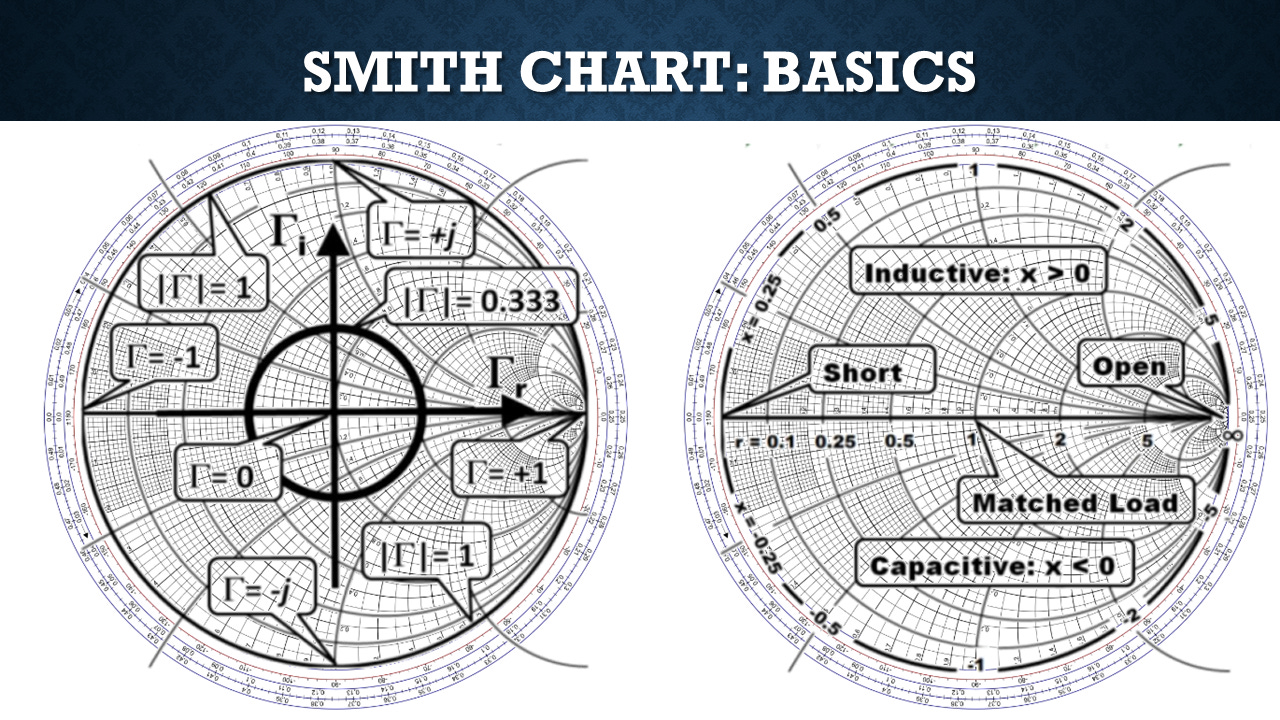
It's effectively a polar plot of the reflection coefficient in complex space for circuits. So if you have a perfectly matched circuit with no reflection, the system that you're at is right there at the bullseye of your Smith chart. If you're on the rim, the magnitude of the reflection coefficient is 1, but it can be plus 1 here. It's complex, so it can be plus j, which electrical engineers use instead of i. You'll minus one there, minus J there.
So it's kind of a bull's eye, in effect, helping an electrical engineer or microwave engineer design a match to an electrical system like an antenna. So over here, at that point, you're dealing with an open on the transmission line. At this point, you're dealing with a short, like the two conductors connected together. Again, the middle is a matched load. If you are above the line, you are inductive or magnetic. If you are below the line, you are capacitive.
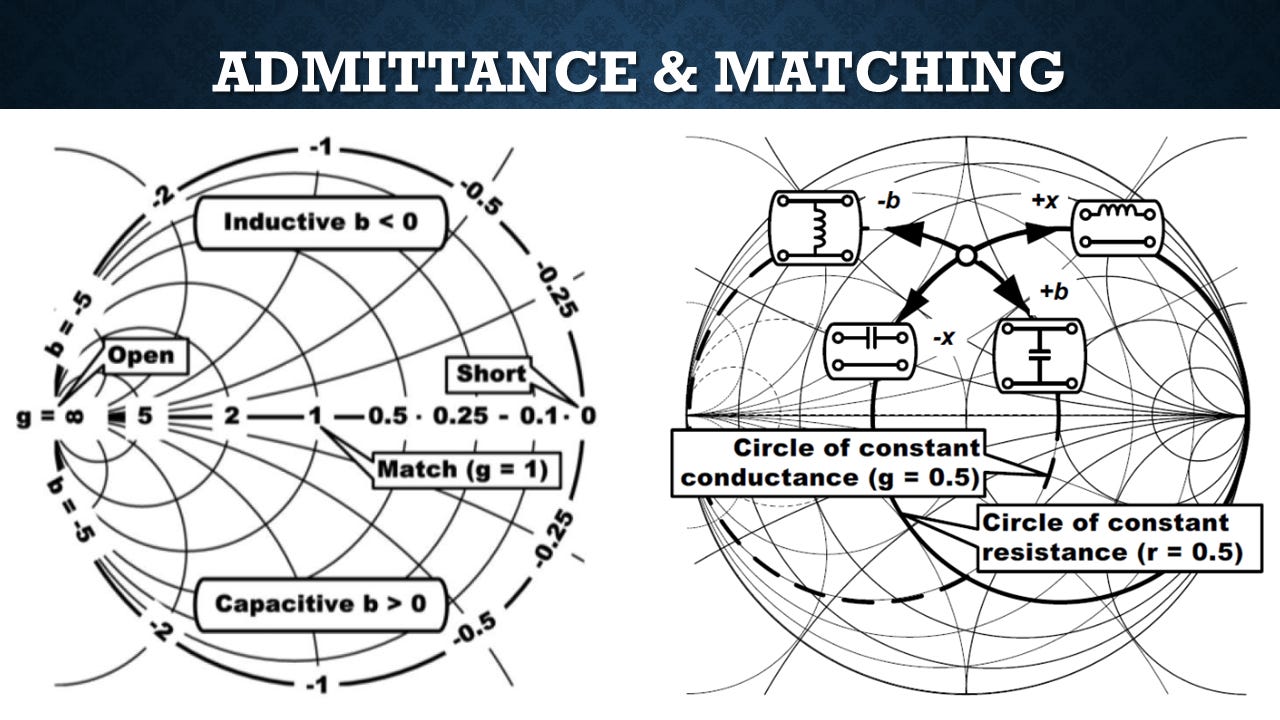
And this is how all these complicated circuit calculations were done before people had computers. They'd draw pictures of them on Smith charts. So what they would do is get an admittance chart, which you get by flipping, the inverse of the Smith chart, they'd lay them both down here. And then if you have a mismatched point that you're trying to get matched to the ideal impedance at the origin, you can add a parallel capacitance to move it this way. You can add a series inductance to move it that way. a parallel inductance that way, and a series capacitance that way.
So by concatenating the capacitors and inductors and series and parallel, you can basically maneuver that point to line it up where you want it to be. It's a very powerful graphical technique. And even with computers, electrical engineers still look at things on Smith charts just because of the power of being able to intuit what's going on.
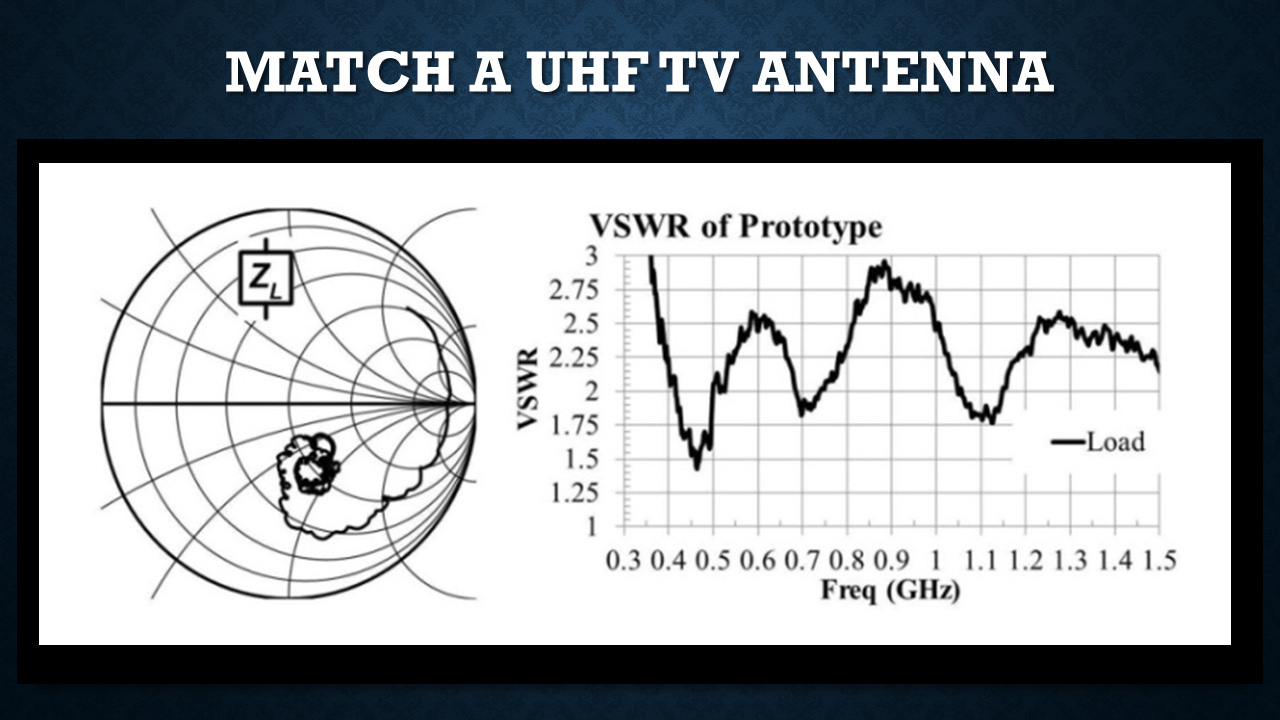
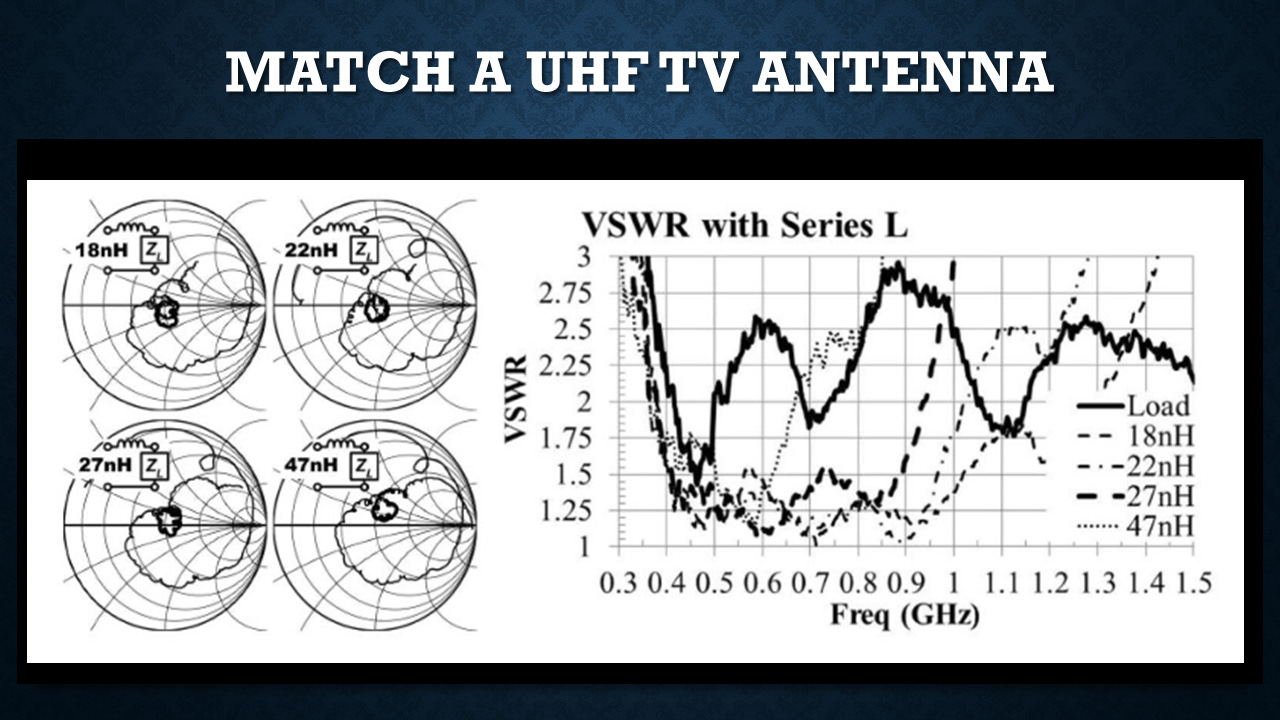
Simple problem. This is a consulting job that I had. I was asked to design a UHF TV antenna. And I designed the antenna. I did my best to make it ultra wide band and with a really good match. But I got this really crappy voltage standing wave ratio. Two is kind of a marginal match. And you can see it's going all over the place there.
But you can see on the Smith chart, it's pretty well localized. And if I'm down here in capacitive territory, if I add a little bit of inductance, I can bring that up and hopefully hit the bullseye. So that's exactly what I did. I tried a couple different inductors in series with the antenna. And you can see how the larger the inductor, the more it got pulled up. And somewhere in between there, before overshooting, I had a really good match.
So that's kind of a practical example of how you would use the Smith chart.
Dipole Impedance
So let's go back to Schelkunoff and his colleague, Harold Friis. Another thing that physicists don't appreciate is Schelkunoff 's colleague, Friis, came up with this equation that's on the board, Friis's equation for working out the received power as a function of the transmit power, knowing antenna properties like the apertures of the antenna and the wavelength and the distance apart they are.
But they focused on the dipole equations, you know, the same equations that are still mentioned in Jackson and Stratton alike, but focused on the complex impedances that you get for an electric and magnetic dipole. This is like on the axis of the dipole.
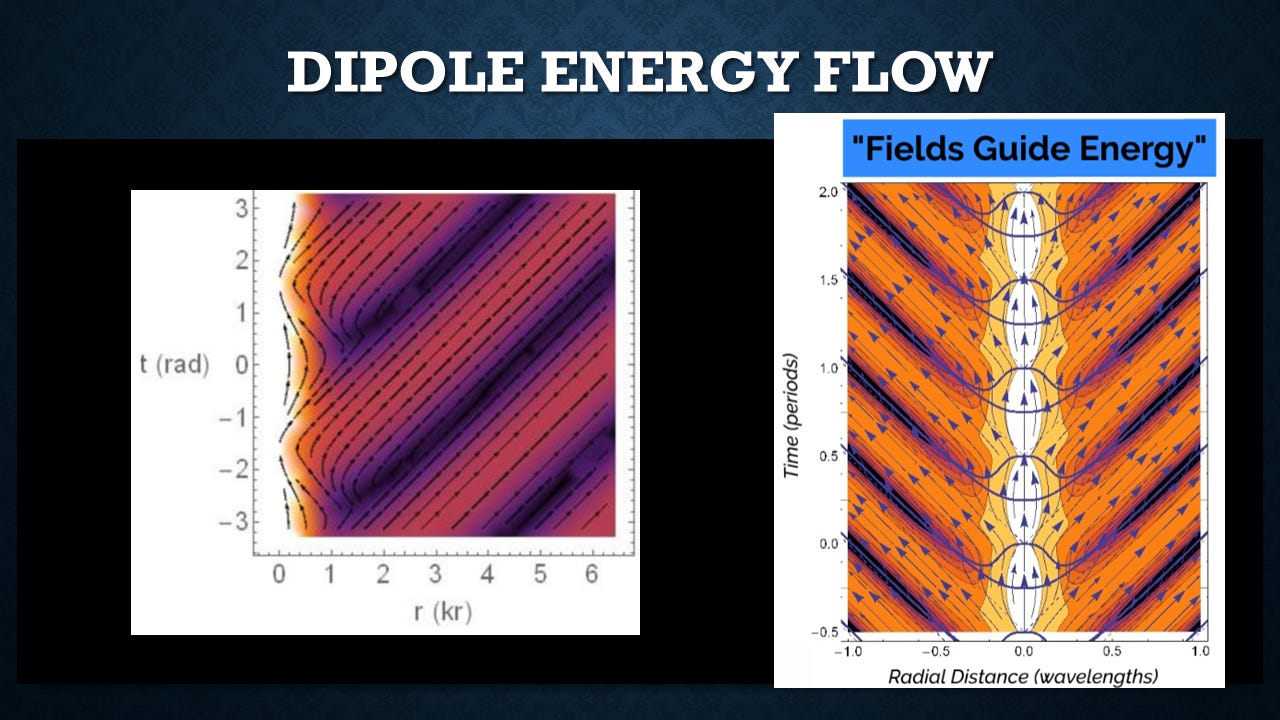
Dipole Energy Flow
And if you take those impedances, and calculate the time domain energy flow, you see some very interesting features. I'll just focus on this diagram on the right. This is a space-time energy flow diagram. The horizontal axis is distance from the dipole oscillator that's at the origin. In the space-time diagram, we scale it so the speed of light is 45 degrees.
So what you see here is energy oscillating in and out close to that dipole, breaking off and then decoupling and moving away. And this is a little bit confusing to someone who thinks in terms of Feynman diagrams, and I've got a point charge, and we jiggle this point charge, and out pops a photon, and it moves away at the speed of light. Because what this is showing is the energy does not move at the speed of light. It's going almost stationary. relatively slowly, and it's only out here like a quarter wavelength or so away that it's decoupling and starting to move at the speed of light.
That radiation process isn't just a point charge spitting out a point photon. It's a much more complex physical process that really isn't appreciated by physicists.
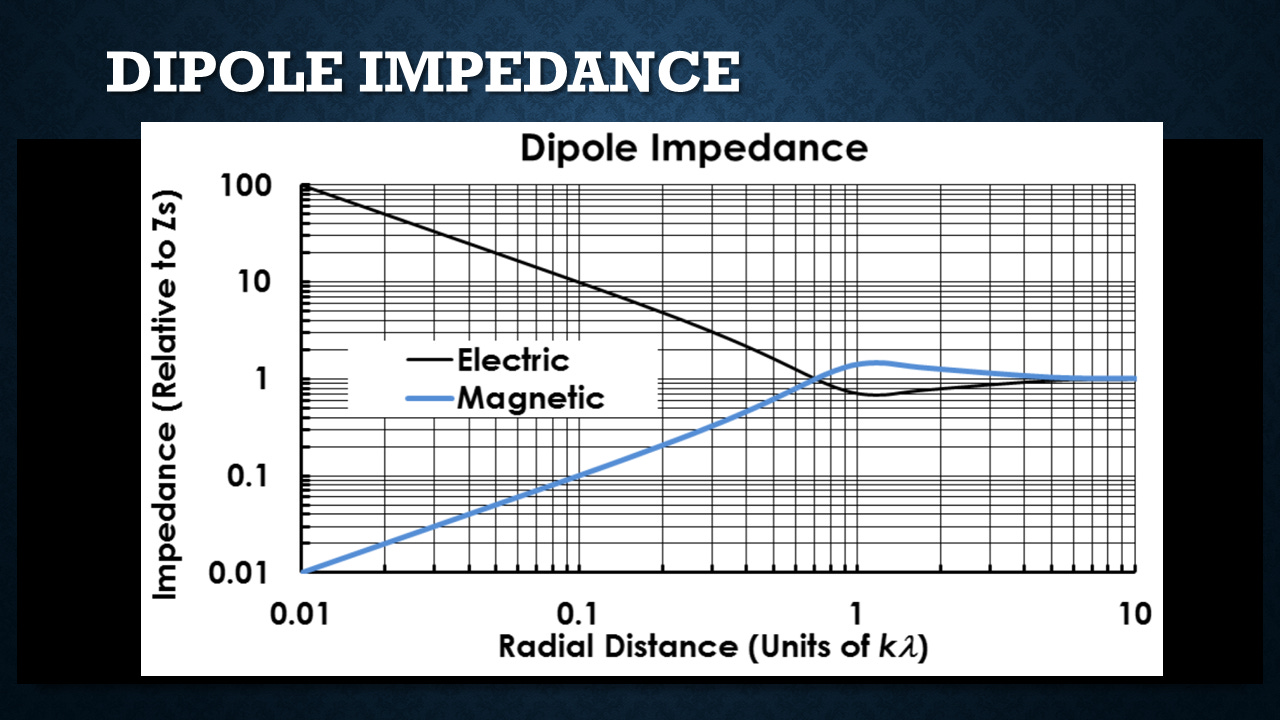
Dipole Impedance
So you can take a look at that dipole impedance And this is scaled to the impedance of free space. So if you're far enough away from the antenna, all the fields are at the impedance of free space. But if you have an electric antenna, you have a very electric impedance up close, very strong electric fields. If you have a magnetic dipole antenna, you have a very low impedance because it's mostly magnetic. Remember, E over H, so if the H is very big, the impedance is very small.
And you can see how they converge by the time. This is about a sixth of a wavelength away. They kind of overshoot. And this is in units of lambda over 2 pi, which are used a lot. So this is about a sixth of a wavelength. And by the time you're about a wavelength or so away, you can see the impedance converges to free space.
Interesting thing is you can look at the phase and the power factor. Now, again, this power factor and these phase differences for reactive fields are things that electrical engineers learn in their basic circuit theory classes. If you go very close to the dipole, the phase difference between the electric and magnetic fields is 90 degrees.
As you move this curve I'm sorry, the top curve, 90 degrees, and then as you move out into the far field, you get closer and closer, that phase being zero, to have the fields aligned and have real power associated with them. Well, there's a power factor associated with that, just like you'd have in an AC power circuit. where you start off not having much real power, and only as you start to get a half wavelength or so away do you have real power flow.
So this whole process of radiation has a great many subtleties that are really not appreciated by physicists.
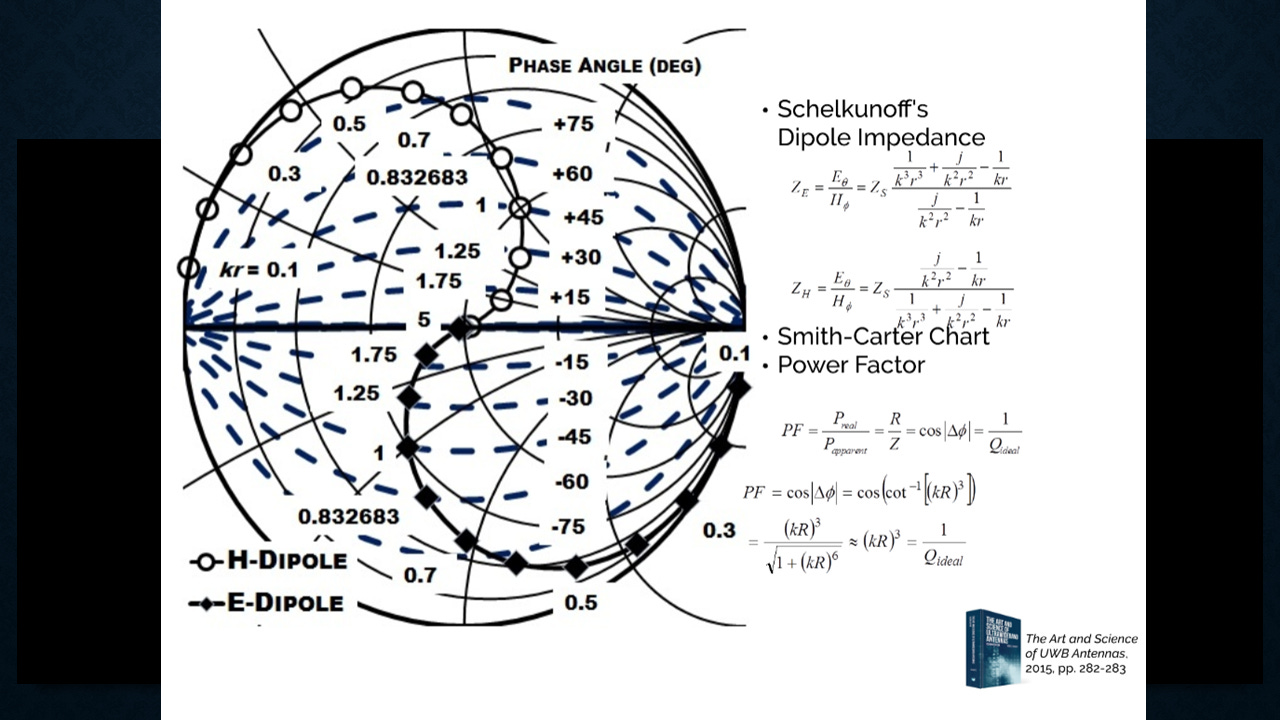
The Schelkunoff-Smith Chart
Now, what you can do is you can take those impedances for an electric dipole or a magnetic dipole, and you can plot them on a Smith chart. Now, this Smith chart is modified. It's actually called a Smith-Carter chart because it shows those phase difference curves. So if you had a plus or minus 90 degree phase curve, it's purely reactive. You're on the border of the Smith chart.
The bullseye there is the 376 ohms free space impedance. As you start to get to kr equal 1, that's a sixth of a wavelength, you have a 45 degree phase difference. As you get out to about 5 times kr, that's about 5 sixth of a wavelength, you're getting pretty well matched.
So you can plot those impedance relationships associated with the radiation of electromagnetic energy from a small antenna on a Smith chart. In fact, I use this as my little personal sigil on my web page; I think it's such a cool diagram.
And if you take a look at that, it helps you calculate that that power factor is just the inverse of the quality factor, and you can work out for a given size of dipole what the efficiency is going to be and what the gain of the antenna is going to be. So just based on knowing the field impedance, the size, and the quality factor, you can tell how good an antenna that you can make and what those limits are.
Electromagnetic Waves and How They Interfere
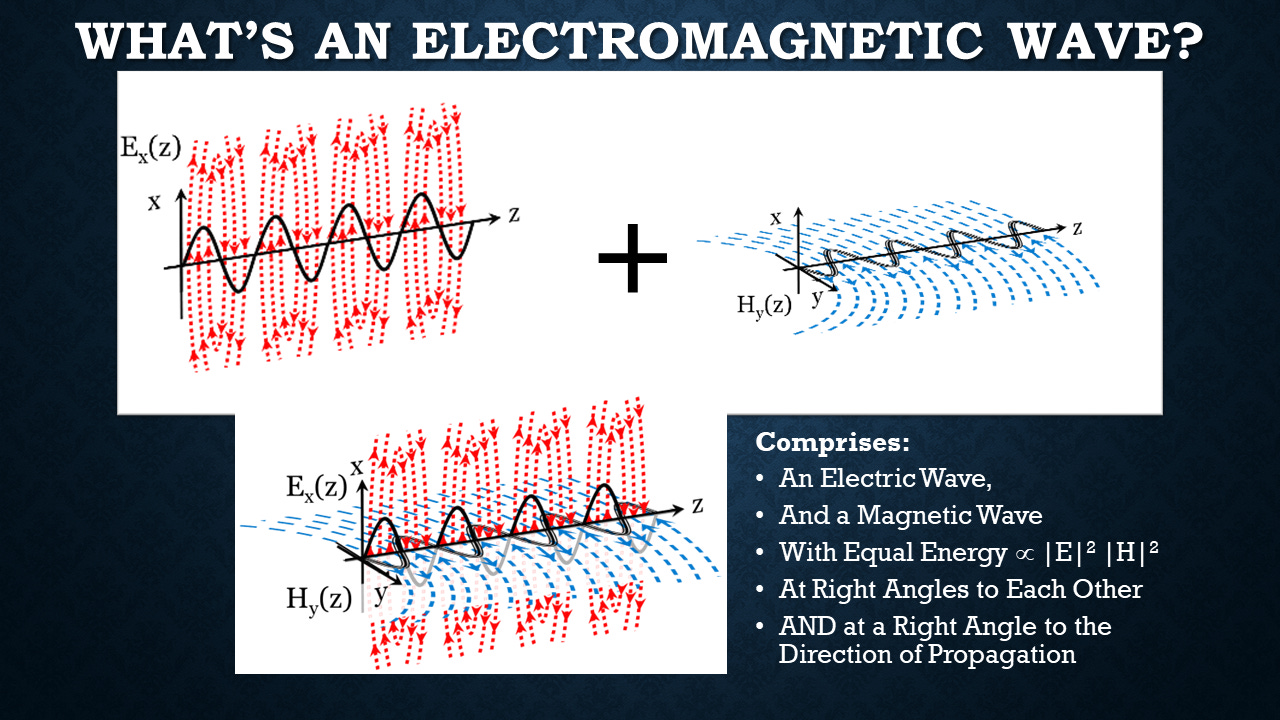
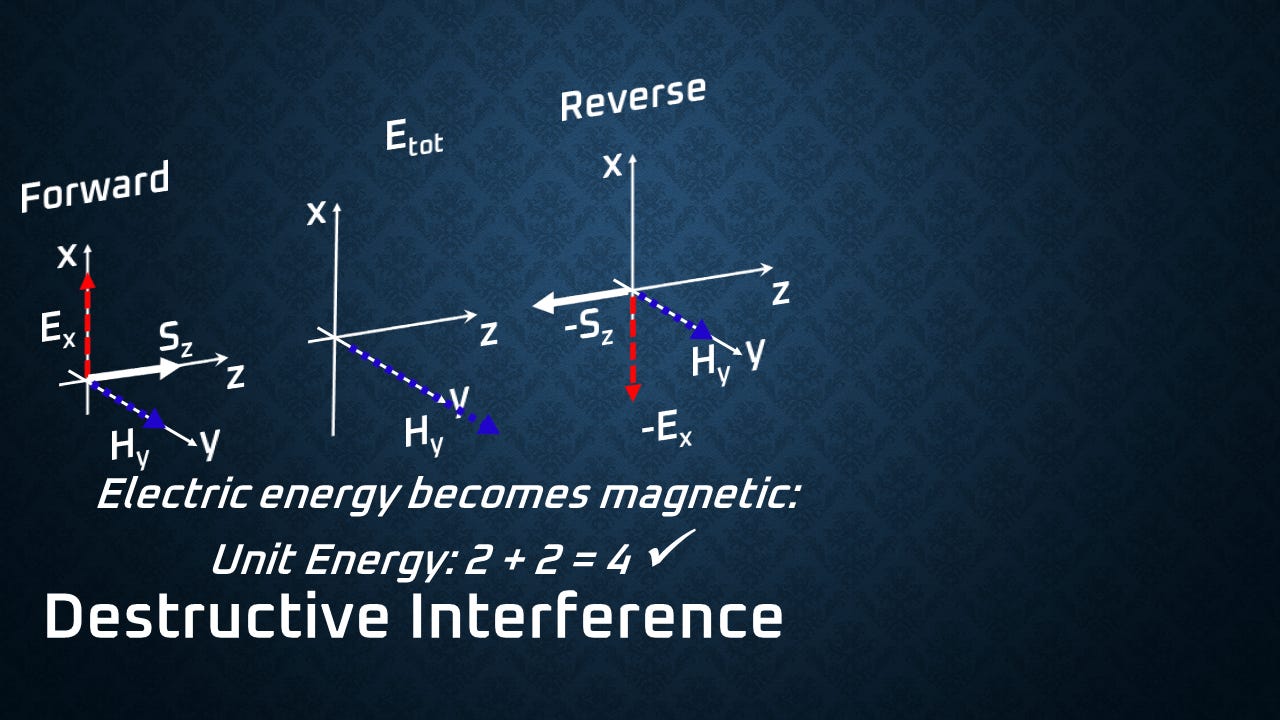
Well, I presented a little bit of this last time, but I want to review because, again, many people just don't understand what an electromagnetic wave is. It's, of course, a combination of an electric wave and a magnetic wave at right angles to each other. Normally, they have equal amounts of energy, equal electric and equal magnetic.
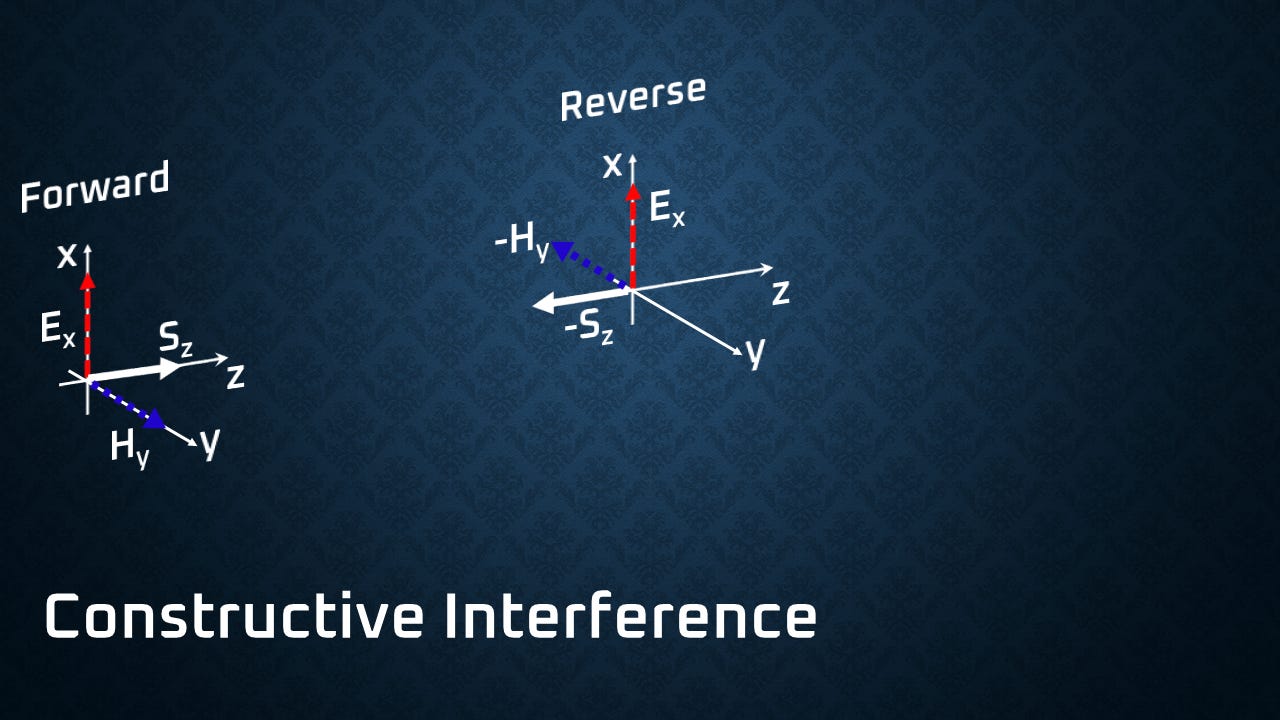
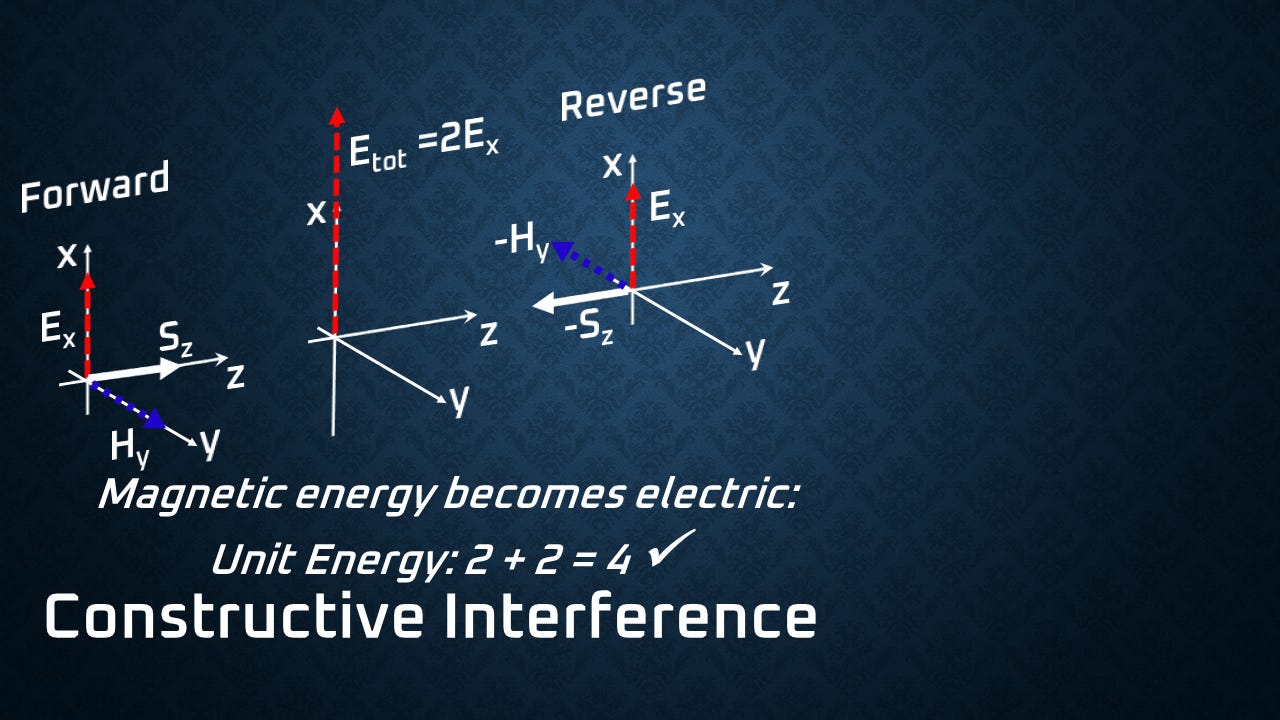
But when you start to interfere, you end up with concentrations of electric or magnetic energy. If you have a constructive interference of two waves coming together, you'll notice you have double the electric field. Well, the problem with that is the energy goes as the field squared, so you have four times the electric energy. But it's not the electric energy that's conserved, it's the total energy.
And you'll notice that the magnetic fields cancel out. Now, if you look at your right-hand rule, E cross H, you can see how the vectors work out there. So in a constructive interference, that balance of electric and magnetic energy becomes purely electric.
If you look at a destructive interference, so now the electric fields are going to cancel out, but what happens is the magnetic field is going to reinforce.
So you have the electric energy turning into magnetic energy. But the thing that's really interesting about this is that the energy is stopping when you have only one field. A static field means the energy isn't moving at all. You know, E cross H telling you the power flow, if E or H is zero, it's not going anywhere.
You can relate that back to the normalized energy velocity. And I had to put some equations in the chart, or they'd revoke my PhD.
The Great Circle of Electromagnetism
So this is an interesting observation that if you take this quantity called the normalized Lagrangian, the difference between the electric and magnetic field energy, and you divide it by the total energy, that is equal to plus one if you are electrostatic, and minus one if you are magnetostatic, and zero if you have a balance of energy that's associated with radiation.
And you can compare that to the normalized energy velocity, where the energy is either going backwards at the speed of light, minus 1, or forwards at the speed of light, plus 1. And if you square those two quantities and add them together, you get the equation of a unit circle.
So all of these one-dimensional problems where electric and magnetic fields are interfering with each other, you can plot on that great circle of electromagnetism. And physicists normally think only in terms of radiation or only in terms of electrostatics. And it's very rare that anyone actually traces exactly what's happening between going from an electrostatic case to radiation.
Or, for instance, a forward wave interacts with an open. It becomes electrostatic. It reflects off of it. It turns around and becomes a reverse wave bouncing off of that open. All that physics is not appreciated by most physicists.
So the key thing is the energy is not following the fields. It's following the superposition of the fields working together. So the waves and the fields always move at the speed of light. We can't have them stopping and then going faster than the speed of light to catch up. What's happening is the energy slows down, stops, and changes direction.
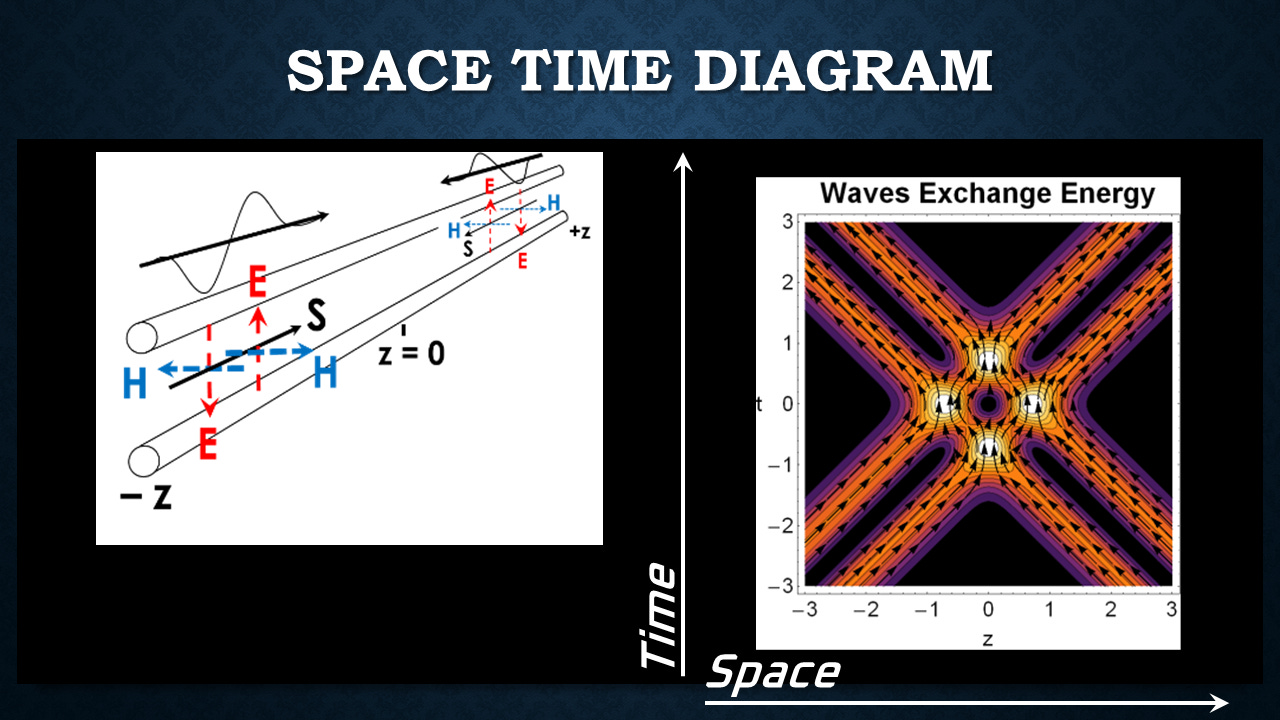
Two Waves Interfering
So, for instance, if we have two waves coming together and we look at how they interact on the space-time energy diagram, we have a goes-down, goes-up wave interfering with a goes-up, goes-down wave. As the two goes-ups interfere, we get an electrostatic node. The energy stops and changes direction. As the two waves align perfectly, they cancel out, and we have a magnetostatic node as the energy comes to a rest. As we pull them apart, the two goes-downs line up electrostatically.
And if you take a look at the energy flow, the two waves pass through each other at the speed of light, but in doing so, they are exchanging energy. And that is a concept that's completely foreign to thinking of electromagnetic waves in terms of just point photons that are moving with fields at the speed of light.
I'm going to run out of time here, so I'm going to have to kind of fast forward through some more complicated examples and just summarize that what physicists don't know about electromagnetism is concepts like impedance, Smith charts, antenna limits, and energy flow, how fields and energy are two different quantities that move in different ways.
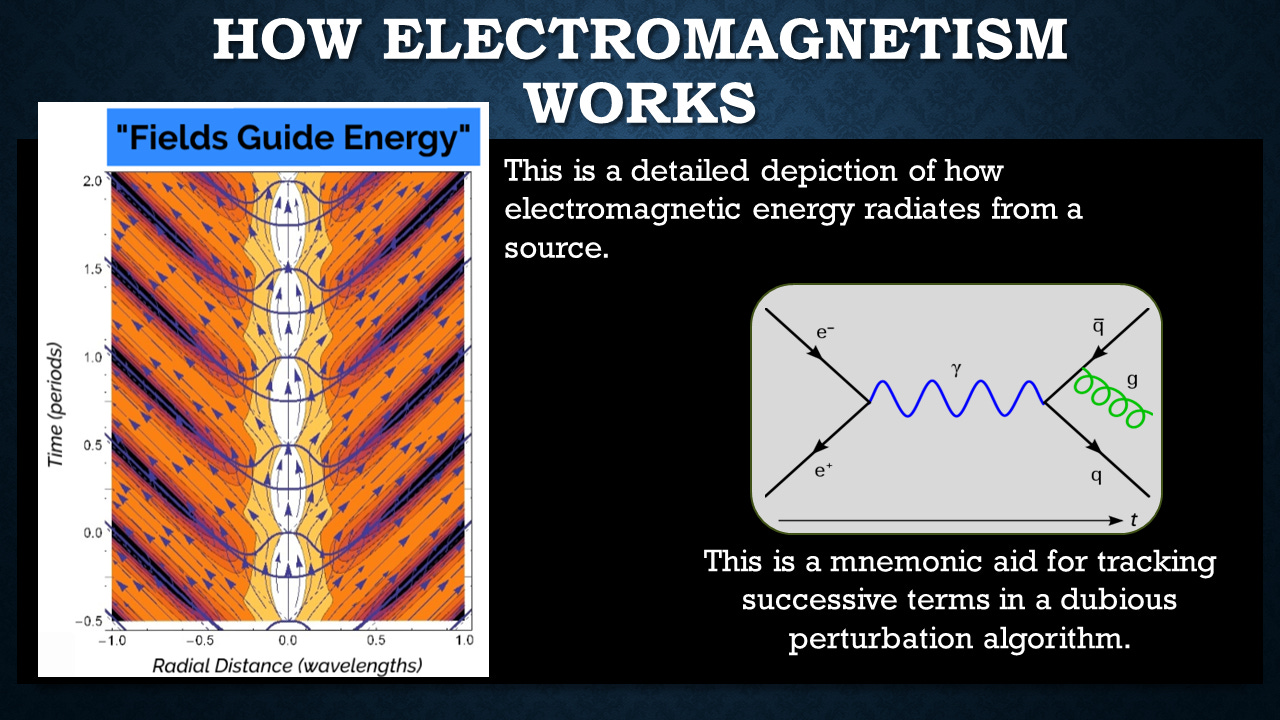
And so looking at something like this, we're looking at how the energy radiates away from a dipole. That's a detailed depiction of how electromagnetic energy radiates from a source. A Feynman diagram is a mnemonic aid for tracking successive terms in a dubious perturbation algorithm. It's not a fundamental picture of the underlying fundamental reality.
What About Quantum Mechanics?
So the key interesting thing here is how this addresses the problem of wave particle duality in the same way Louis de Broglie proposed way back in the 1920s with his pilot wave theory.
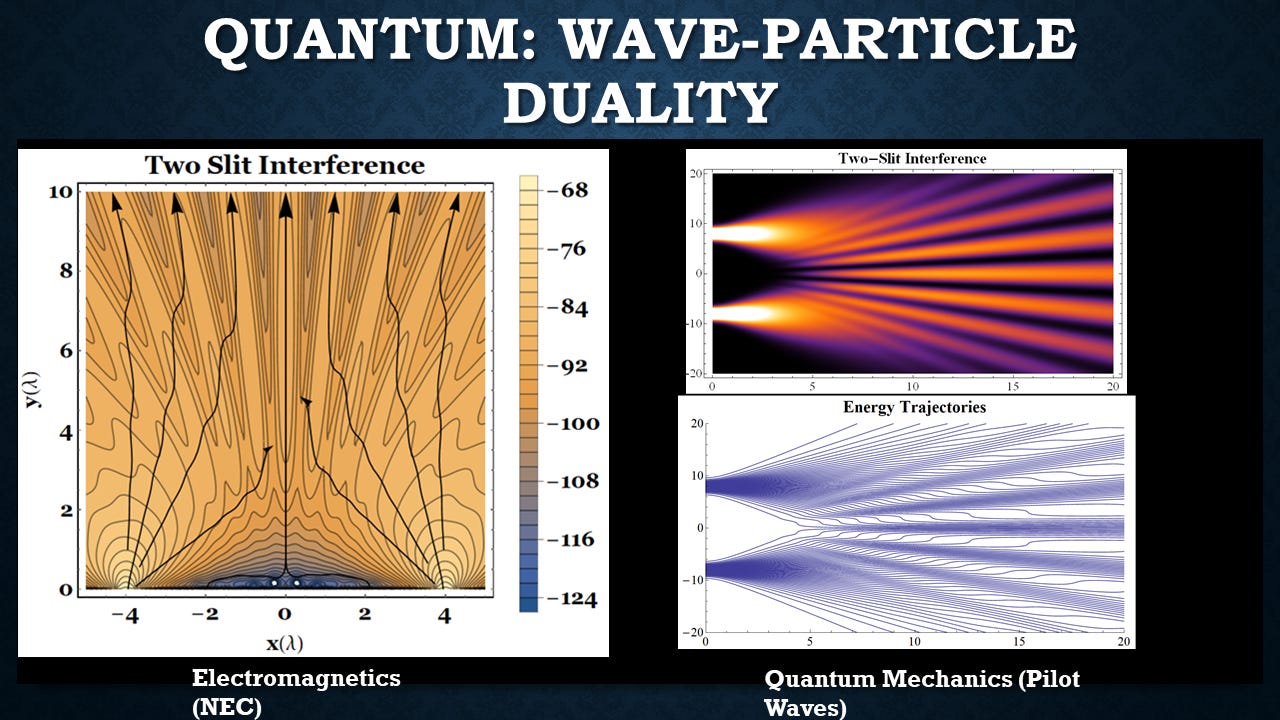
The concept that, as he described it, a photon coming from one laser or the other interfering is guided by the superposition of the waves emitted by the two lasers. And that solves, for instance, the paradox of the two-slit experiment. where you have the superposition of waves going through both slits, guiding the photon through one or the other on a particular distinct path.
You can see an electromagnetic calculation I did showing the energy flow in a two-slit interference and the predictions of the pilot waves for how those trajectories work in a two-slit experiment doing the calculation quantum mechanically. And they're qualitatively very similar.
So if you have the two slits, The fields go through both slits. They generate an interference pattern with many possible trajectories. And then as a photon goes through, it happens to pick one of those trajectories and end up in the interference pattern on the screen.
Want to Learn More?
So if you're interested in learning more about this novel take on physics, You can see a lot of this in my book, The Art and Science of Ultrawideband Antennas, which I probably should have subtitled An Introduction to Time Domain Electromagnetics and Energy Flow, because that's really the key concept that underlies that.
A lot of the fundamental ideas, including that great circle of electromagnetics and how that plays out in a variety of problems, are in this article from the Philosophical Transactions of the Royal Society of London from 2018. That's available free and online.
Again, I recommend Oliver Konza's article on the state of QED if you want to understand and go into more detail on the remarkable way in which that theory was devised.
I will plug my book sale that I coordinate that's running right now. You can go to my website, ethersar.com. There are almost 200 books there that are free or 99 cents from fellow indie authors, including the first book in my series, The Hidden Truth. If you like alternate history conspiracy techno thrillers, that's the series for you.
And more recently, my latest project is The Wise of Heart, a modern day reimagining of the Scopes trial amid the transgender mania. So a high school biology teacher decides to serve a test case for a law mandating not teaching the biology of sex in favor of having mandatory gender affirmation. And the resulting trial attracts national attention from Major politicians and a media circus reporting on it.
And ironically enough, this story about a high school teacher getting silenced for teaching the biology of sex kind of played out in real life. Because after the project was fully funded on Kickstarter, Kickstarter canceled it. So I replatformed on a site, “fundmycomic.” I can't say enough good things about those people. I ended up with well over double what I had when Kickstarter canceled me, thanks to the resulting publicity on everywhere from Fox News and The Blaze and bounding into comics and upstream reviews.
I'm glad to report that the books arrived yesterday just in time. And I'm going to begin fulfilling to the backers. I've already fulfilled two copies to backers who happen to be here. And there will be copies available on Author's Alley from 6 to 9 o'clock tomorrow, where I have my book sale and signing.
So if you're interested in contacting me, my contact information is here. And I'll leave that up while I ask if there are any questions. Yes?
Questions:
Am I the only one looking at the development of QED and thinking of circles and epicycles?
I had no idea when I went through grad school the shaky foundation that it was on. I mean, it's very few people, if any, can follow the calculations. They are not reported in enough detail in a journal article for anyone to be able to follow along and check their accuracy. Even back in the 1950s, we saw the simple calculations sliding past all the best physicists in the world for a half dozen years before anyone noticed there was a problem.
And really, they only noticed there was a problem because the experimental result was getting out of line with the theory, and that prompted a second look at it. I do not trust QED at all as being a fundamental theory of how electromagnetics works.
I guess we need a Kepler.
I'm sorry?
I guess we need a Kepler.
Yes, we do. Yes.
If you don't trust it, how do you break it?
Well, I think it's broken. You just need to come up with a better explanation for how it works.
This is HDI. How can you create an experiment where the QED people can't get the answer every time?
I don't think you can.
The muon data is already doing that.
Well, yeah. But you can arbitrarily fit at least one set of data, the electron data. But yeah, as Jeff points out, the muon data is inconsistent with how QED works. So there's clearly a problem with QED. The only question is, what's the replacement theory, or how can we fix that problem and come up with the right answer that will apply to both electrons and muons?
Yes?
Well, speaking of somebody who's a complete civilian, the one thing that strikes me is it's almost like they're trying to fit the equation to the experiment not understand what caused the experiment to have that value, and then from that divide...
And that is a long-standing problem in physics that I talked about in a little more detail last year in my talk, but when Heisenberg first came up with his matrix methods for dealing with quantum mechanics back in the 1920s, effectively you had an input or a starting state vector, you applied a matrix to it, you got an output state. There was no physical picture about what's going on. It was a mathematical black box, and it worked. It got the right answer.
And then de Broglie took a look at that, and he was having trouble following it, and he had the brilliant observation, you know, Einstein got the Nobel Prize for demonstrating the photoelectric effect for demonstrating that light had a particle-like nature. If light has a particle-like nature, maybe particles have a light or a wave-like nature. And he came up with his idea of a de Broglie wavelength associated with the electron. And yeah, that worked brilliantly.
And then Schrodinger took that and came up with the Schrodinger equation. And all of a sudden, you had a picture of quantum mechanics where you kind of sort of saw there's things that are happening in space that we can assign to particular locations in particular, probability densities, and so forth.
But it's kind of a long story that I don't have time to answer here that I addressed last time. But there was a profound philosophical prejudice against that perspective. I got to talk with John Wheeler, who was Feynman's PhD advisor and a noted expert on quantum measurement theory in his 80s, proudly proclaiming he would go anywhere to understand quantum theory. He doesn't have to worry about his reputation. He'll entertain any idea, no matter how wild, to try to answer the problems associated with quantum measurement.
And I asked him, so what do you think of pilot wave theory? And he said, the screwdriver theory of quantum mechanics. I kind of scratched my head about that and said, well, have you written some more analysis of this that I could read, understand why you don't like it? His answer to me was, you know, I really ought to look into that sometimes so I can tell what's wrong with it.
And I don't think he was alone in that attitude. I think a great many, in fact, most physicists had the attitude that Bohr and Heisenberg and the Copenhagen interpretation and all the quantum subjectivism was the rule of the day and it was only the poor reactionary people who could not grasp the wondrous nature of their mystical quantum interpretations who were having trouble with this and needed the screwdriver theory and the epicycles of pilot waves to explain it for them and make them have their security blanket to make them comfortable with quantum mechanics.
Yeah, that's definitely the case. Any other questions? Yes.
Unintelligible…
Yeah. Oh, it pops up all over the place. That's a very natural thing to do. Right, but it makes sense. But then... It is calculated from adding up contributions due to various Feynman diagrams. And I showed a picture of, was it the C C2 or C3, where it's a handful of a dozen or so diagrams. And it took some very brilliant people a couple years to crank through them all.
By the time you're getting to C4 and C5, I think it was something like 72,000 separate Feynman diagrams that you have to run through and catalog. And that's why it took a supercomputer to go and do that. And then you have to worry about, yeah, and are you being consistent in how you're removing your You know, renormalizing and removing the infinities. And if you do it a little different way, you're going to get a different answer. And what's the right way? Well, which way agrees with the experiment? That's the right way.
We have about five minutes left. Any other questions in the back? Yes.
There was a physical interpretation or a liquid drop version of pilot wave theory that people were looking at that subsequently had some issues. The reason most people, most physicists I've talked to about this reject pilot wave theory is when you start to try to apply it to many body problems. All of a sudden, it turns out to no longer be waves in three-dimensional space that make lots of intuitive sense. It's all kinds of waves added up in some abstract phase space representation.
And frankly, knowing how hard it is even classically to address what's called the three-body problem or the lunar problem. It took some very solid math, which frankly is beyond me, just to handle the three-body problem of correctly calculating the lunar orbit and all the perturbations that you get between the sun and the earth tugging on it.
Many body problems are very complicated. You know, the fact that a many body pilot wave problem is very complicated doesn't convince me that it's not the right approach.
Yes?
Are magnetic monopoles possible?
Not if, you know, Gauss's law of magnetism is correct, which has been tested to a pretty high degree of accuracy. Now I know people have come up or have found some anomalous results that they like to interpret as magnetic monopoles. So it's possible, but I don't think there's convincing evidence for it.
Yes?
It's more of an observation and a question. I mean, this issue of when you take a perturbation theory and you start adding terms and it sort of becomes, it gets a little better for a while and then if you have more terms, it gets a little worse is not unique to this franchise.
Yeah, that's, yeah.
To make an example, you know, when you take the major scope situations for fluid as well and you start looking at extending them into a lower or lower half of each regime, when you add the first direction terms, it makes it better. When you have the second correction, the fifth is a little better. When you have the third and beyond the correction, the fifth is dramatically worse.
Right. And that's just the universe telling you that that's because you're trying to extend the theory beyond the domain in which the assumptions of the theory apply and you should do something else.
Right. And I think what quantum electrodynamics is telling us is you should do something else.
Yeah.
Okay. Our time is up. Thank you for being such an attentive audience. Thank you.
Enjoyed the post, but maybe not quite enough to spring for a paid subscription?
Then click on the button below to buy me a coffee. Thanks!
Follow Online:
You may follow me online in other places as well:
Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞
Gab: @aetherczar
Twitter: @aetherczar
Amazon: Hans G. Schantz