5.2 Relativity

A Top-Down, or a Bottom Up Theory?

In this philosophic environment, an obscure German-born clerk working in the Swiss patent office had a clever idea. An enthusiastic reader of Poincaré’s 1902 treatise, Science and Hypothesis [[iii]], Albert Einstein (1879–1955) realized that the emerging discoveries in electrodynamics could be explained by two principles: first that the laws of physics are identical in all non-accelerating frames of reference, and second, that the speed of light (in a vacuum) is the same for all observers independent of the motion of the light source or observer [[iv]]. From these two principles, he derived the Lorentz transforms for which Hendrik Antoon Lorentz (1853–1928) had required eleven postulates.

Figure 5.7: In 1905, a young patent clerk, Albert Einstein (1879–1955), introduced the special theory of relativity [[i]], left, and Hermann Minkowski (1864–1909) [[ii]], right, Einstein’s math professor who pioneered the use of space-time diagrams.

In the new form of geometry Einstein proposed, lines of simultaneity (or constant time) and lines of co-spatiality (or constant position) depend upon the relative motion of the observer and change between different inertial reference frames. “Henceforth space by itself and time by itself are doomed to fade away into mere shadows and only a kind of union of the two will preserve an independent reality,” declared Einstein’s math professor, Hermann Minkowski (1864–1909), who followed up and extended upon his student’s work by formalizing the implied four-dimensional geometry [[v]].

Figure 5.8: Space-time diagrams showing relative motion of a moving observer from our rest frame (left), and the moving observer’s perspective from his own frame (right).

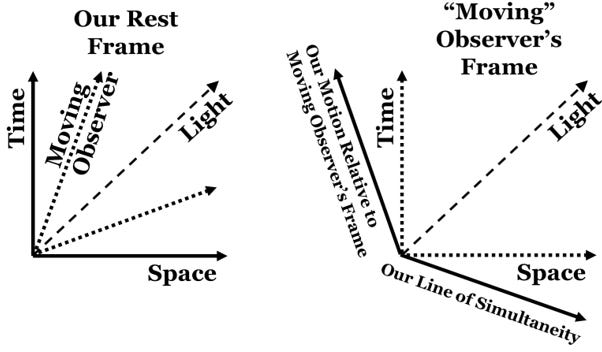
Figure 5.8 illustrates special relativity using space–time diagrams. By convention, the vertical axis denotes time and the horizontal axis, space. The axes are scaled so light travels at 45 degrees with unit slope. An observer at rest follows a vertical path in space-time, traversing time, but not space. A moving observer with constant velocity travels at less than the speed of light, with a space-time trajectory at a velocity slower than and a slope greater than light. From the moving observer’s perspective, he is at rest, and we are moving backwards with respect to him. Because of this relative motion, the moving observer sees different points in space–time as simultaneous. His space axis tilts relative to the space axis of our rest frame. The net effect is that the speed of light appears the same in both reference frames.

That is a very abstract way of looking at relativity and its implications, so consider a more down-to-earth example. A farmer asks his farm hand to make a 20-meter ladder fit in a 10-meter barn. Fortunately, his farm hand is a sprinter capable of running far faster than usual – so fast that he can run at 90% of the speed of light. The farm hand grabs the ladder, and runs toward the barn, at 90% the speed of light. What is the farmer’s perspective? And what does the farm hand see?

The farmer standing by the door sees the farm hand pass by with the ladder. Because the ladder is moving so quickly relative to the speed of light, the farmer doesn't perceive both ends of the ladder as they are simultaneously in the ladder’s frame. Instead, he sees them at slightly different times due to the ladder’s rapid motion. Whether the ladder is approaching or receding, from the farmer’s perspective, the ladder, 20 meters long when at rest, appears to have a length of only 8.7 meters.

Figure 5.9 Ladder-and-barn paradox from the perspective of the farmer standing next to the barn (left), and from the perspective of the swift farm hand carrying the ladder (right) [[vi]]. Process times, below.

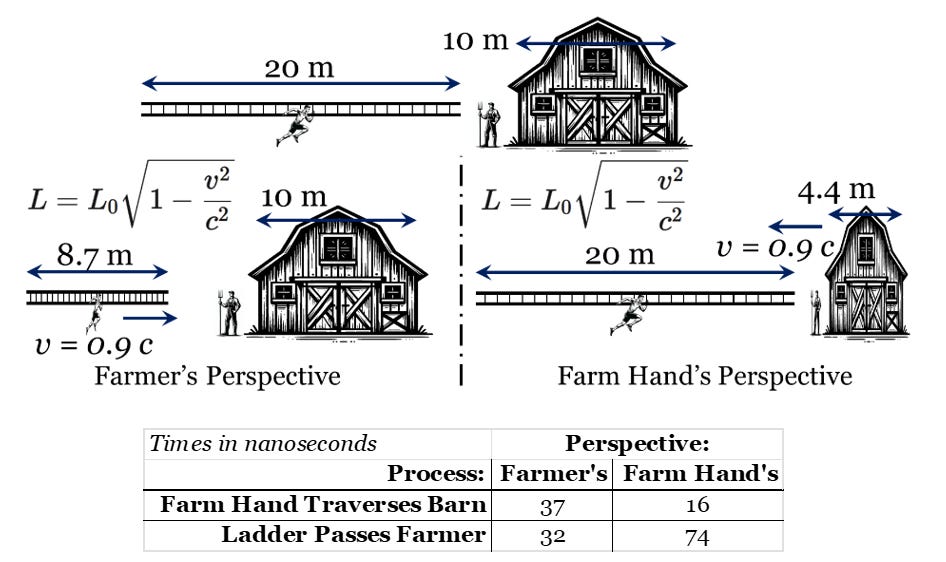
Of course, the farm hand perceives a different scenario in which the barn appears far shorter than the ladder. Because the barn is moving at 90% of the speed of light from the farm hand’s perspective, the 10-meter barn now appears only 4.4 meters wide, far too small to contain the ladder. Since the farmer pays his salary, if it makes his boss happy, the farm hand won’t complain.

Notice that this length contraction is also associated with a time dilation. The farmer sees his farm hand traverse the 10-meter barn in 37 nanoseconds, and the ladder passes by the farmer in 32 nanoseconds. From the farm hand’s perspective, he traverses the 4.4-meter barn in 16 nanoseconds and the ladder passes by the farmer in 74 nanoseconds. One clock says one process takes less time than the other. The other clock says the other process takes less time. Whose clock is correct?

The ladder-and-barn paradox illustrates how different observers perceive different events at different relative times [[ix]]. The clock paradox is arguably the most controversial and troublesome aspect of relativity. In 1963, the American Association of Physics Teachers compiled a volume on special relativity theory [[x]], including sixteen papers on relativity theory – half of which specifically addressed the clock paradox or a particularly dramatic example of it, the twin paradox [[xi]]. Premise of some excellent science fiction [[xii]], Einstein alluded to it in his original paper.

Figure 5.10: Spacetime diagram for the twin paradox [[vii]], left, and astronauts make ready to depart in a giant projectile to be shot to the moon from a gun in Jules Verne’s 1865 classic, From the Earth to the Moon [[viii]].

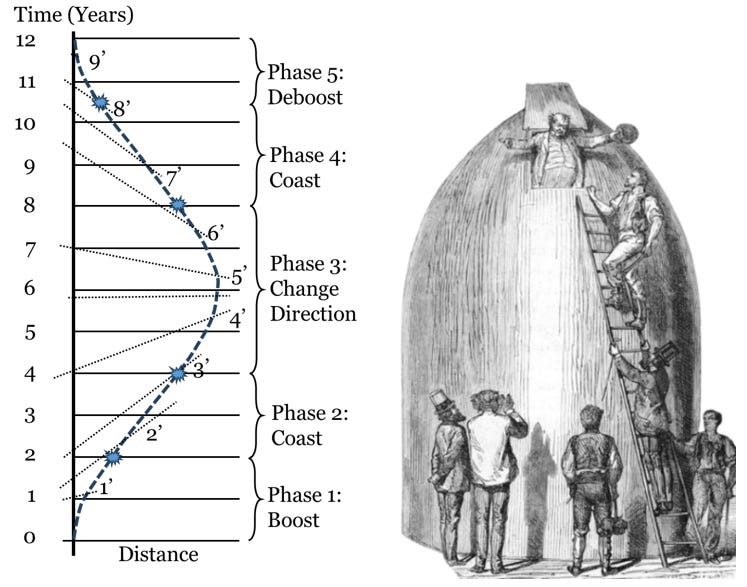
Consider an astronaut who bids his twin brother farewell and departs for a journey on a very fast rocket ship at time zero. From the perspective of his Earth-bound twin brother, the astronaut accelerates or boosts for two years, coasts for two years, decelerates to change direction and return home for four years, coasts for a little more than two years, and deboosts for just under two years, coming to a rest in orbit around the Earth for a total journey of a dozen years. From the astronauts’ perspective, however, the trip required only nine years, and his twin brother has aged three additional years on his return.

Recently, real-life astronaut, Scott Kelley (1964 –   ), spent a year on the International Space Station and returned an estimated 13 milliseconds younger than the twin brother he left behind [[xiii]]. Such a small difference may not appear to be of any practical significance. However, the Global Positioning System (GPS) and similar systems like the European Galileo, Russian GLONASS, and Chinese BeiDou systems rely on precise timing of radio-wave signals. Light travels a foot (30 cm) in a nanosecond, and an error in timing of 13 milliseconds could correspond to a location error of ten kilometers or six miles. Thus, satellite navigation systems must worry about maintaining timing accuracy of nanoseconds or better.

We've already seen how Fitzgerald, Larmor, Poincaré, Lorentz, and others had already worked out the fundamentals of special relativity before Einstein submitted his paper. In fact, until 1920 or so, it was often called the "Lorentz-Einstein" theory of special relativity, because of Lorentz's earlier publication of the mathematical transforms at the heart of the theory. What was Einstein's contribution? Why did he ultimately end up with the bulk of the credit?

We can start with two reasons. First, Einstein deduced the theory in a novel way: top-down from two fundamental principles. Further, he validated it with a host of thought experiments. Many found his approach more compelling than the traditional bottom-up approach of looking to electrodynamic experiments and theory to infer electrodynamic behavior at speeds approaching the speed of light. Second, while the conventional wisdom was to look at relativity in the context of electrodynamic behavior, Einstein argued that relativity was a fundamental principle of all physics. He argued relativity described the fundamental observer dependence of the space-time geometry of reality. His predecessors looked at relativistic effects more narrowly as the consequence of electrodynamic effects in motion at high velocities with respect to the fixed æther of space.

What was the meaning of relativity? What were the implications for how reality works and the mechanism by which light propagates through free space? Not even Einstein was consistent on those questions. His 1905 paper included a bold claim: “The introduction of a ‘luminiferous æther’ will prove to be superfluous inasmuch as the view here to be developed will not require an ‘absolutely stationary space’ provided with special properties… [[xiv]]”

Many years later in 1919 (when he had become famous), he confirmed this position to a New York Times reporter:

There is no æther, as hitherto conceived by science, which is proved by the well known experiment of the celebrated American savant, Michelson, showing that no influence by the motion of the earth on the æther is perceptible through change in velocity of light, such as ought to be produced if the old conception were true” [[xv]].

Einstein’s friend, Paul Ehrenfest (1880–1933), invited Einstein to become a visiting professor at the University of Leiden (in the Netherlands) [[xvi]]. In Einstein’s inaugural lecture, delivered October 27, 1920, he revived the æther, that “sick man of theoretical physics” [[xvii]]. Einstein declared:

“Recapitulating, we may say that according to the general theory of relativity space is endowed with physical qualities; in this sense, therefore, there exists an æther. According to the general theory of relativity, space without æther is unthinkable; for in such a space there not only would be no propagation of light, but also no possibility of existence for standards of space and time (measuring rods and clocks), nor therefore any space-time intervals in the physical sense [[xix]].”

Perhaps it wasn’t the electromagnetic æther “as hitherto conceived by science,” but in 1915, Einstein, himself, had resurrected a very similar æther of sorts in his theory of general relativity (about which we will have more to say shortly). A lecture in Leiden, Lorentz’s hometown, at the behest of Lorentz’s successor, Ehrenfest, was a good opportunity for Einstein to emphasize his version, perhaps in deference to Lorentz who still subscribed to the older æther theory.

Figure 5.11: Paul Ehrenfest (1880–1933), left, his son, Paul Junior, center, and Albert Einstein, right, circa 1920 [[xviii]]. Not pictured is Ehrenfest’s other son, Vassily, who was disabled by Down syndrome.

Einstein’s flirtation with an analogy between the curvature of space and the æther did not last, however. Einstein and his collaborator, Leopold Infeld (1898–1968), writing in The Evolution of Physics in 1938 declared:

The result [of the Michelson-Morley experiment] was a verdict of 'death' to the theory of a calm-ether-sea through which all matter moves... More artificial theories have been tried out... But they all failed ! ... All assumptions concerning ether led nowhere ! The experimental verdict was always negative... Our attempts to discover the properties of the ether led to difficulties and contradictions. After such bad experiences, this is the moment to forget the ether completely and to try to never mention its name [[xx]].

Physicist Gerald James Holton (1922–  ) noted “…everyone – from the extreme positivist to the critical realist – can find some part of Einstein’s work to nail to his mast as a battle flag against the others” [[xxi]]. Let’s take a deeper dive into these contradictory pronouncements to understand how the theory of relativity arose and what were its philosophical influences.

Next time: 5.2.1 Origins of Relativity: Or How to Hide Your Sources

Enjoyed the article, but maybe not quite enough to spring for a paid subscription?
Then click on the button below to buy me a coffee. Thanks!

Full Table of Contents [click here]

Follow Online:

You may follow me online in other places as well:

• Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞

• Gab: @aetherczar

• Twitter: @aetherczar

• Amazon: Hans G. Schantz

• Wise of Heart Substack

• ResearchGate

• Google Scholar

• ORCID

---

References

---

[[i]]         By Lucien Chavan [1] (1868 - 1942), a friend of Einstein's when he was living in Domain, https://commons.wikimedia.org/w/index.php?curid=16699199

[[ii]]        Photograph of Hermann Minkowski. This is a detail of page 5 of the historical document: Raum und Zeit (Jahresberichte der Deutschen Mathematiker- Vereinigung, Leipzig, 1909). See: https://en.wikipedia.org/wiki/File:De_Raum_zeit_Minkowski_Bild.jpg

[[iii]]       Darrigold, Oliver, “The Mystery of the Einstein- Poincaré Connection,” Isis, 95(4), December 2004, pp. 614-626. DOI: 10.1086/430652.

[[iv]]        Einstein, Albert, “Zur Elektrodynamik bewegter Körper,” (“On the Electrodynamics of Moving Bodies”), Annalen der Physik, vol. 17 no. 10, 1905, pp. 891–921.

[[v]]        Lorentz, Hendrik Antoon; Albert Einstein; Hermann Minkowski; Arnold Sommerfeld; Hermann Weyl; The Principle of Relativity: A Collection of Original Memoirs on the Special and General Theory of Relativity, New York: Dodd, Mead and Company, 1923, p. 75. “Space and Time,” by H. Minkowski, A Translation of an Address delivered at the 80th Assembly of German Natural Scientists and Physicians at Cologne, 21 September 1908

[[vi]]        Weideman, Tom, “The Ladder & Barn Paradox,” LibreTexts: Physics. “The LibreTexts libraries are Powered by NICE CXone Expert and are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739.” See: https://phys.libretexts.org/Courses/University_of_California_Davis/UCD%3A_Physics_9D__Modern_Physics/2%3A_Foundations_of_Special_Relativity/2.4%3A_Paradoxes .

[[vii]]       “Twin paradox employing a rocket following an acceleration profile in terms of coordinate time T and by setting c=1: Phase 1 (a=0.6, T=2); Phase 2 (a=0, T=2); Phase 3-4 (a=-0.6, 2T=4); Phase 5 (a=0, T=2); Phase 6 (a=0.6, T=2). The twins meet at T=12 and τ=9.33. The blue [unprimed] numbers indicate the coordinate time T in the inertial frame of the stay-at-home-twin, the red [primed] numbers the proper time τ of the rocket-twin, and "a" is the proper acceleration. The thin red lines represent lines of simultaneity in terms of the different momentary inertial frames of the rocket-twin. The points marked by blue [primed] numbers 2, 4, 8 and 10 indicate the times when the acceleration changes direction.” After: https://en.wikipedia.org/wiki/Twin_paradox#/media/File:TwinParadoxProperAcceleration.svg

[[viii]]      Verne, Jules, De la terre à la lune, 1865. See: https://upload.wikimedia.org/wikipedia/commons/2/20/Delaterrelalun00vern_0155_1.png

[[ix]]       Taylor, Edwin F., John Archibald Wheeler, Spacetime Physics: A Brief, Readable Exposition of Modern RELARVITY THEORY Illustrated and Amplified by a Wealth of PROBLEMS, PUZZLES, and PARADOXES and Their Detailed Solutions, 1^st ed., New York: W.H. Freeman & Company, 1966, p. 70, solution on p. 9 of solutions appendix. See the 2^nd ed, here: https://amzn.to/4gYEWFM

[[x]]        Holton, Gerald, Special Relativity Theory, Selected Reprints, New York: American Association of Physics Teachers, the American Institute of Physics, 1962. See the Table of Contents, p. 9.

[[xi]]       Lasky, Ronald C., “How Does Relativity Theory Resolve the Twin Paradox?” Scientific American, March 17, 2003. See: https://www.scientificamerican.com/article/how-does-relativity-theor/

[[xii]]       Heinlein, Robert A., Time for the Stars, New York: Charles Scribner’s Sons, 1956. See: https://amzn.to/4eKusIy

[[xiii]]      Anthony, Andrew, “Interview – Scott Kelley: ‘I came back from space younger than my twin,’” The Guardian, October 29, 2017. See: https://www.theguardian.com/science/2017/oct/29/scott-kelly-astronaut-interview-space-younger-twin-endurance

[[xiv]]      Einstein et al, The Principle of Relativity: A Collection of Original Papers on the Special and General Theory of Relativity. Notes by A. Sommerfeld, New York: Dover Publications, p. 38. Reprint of 1923 Meuthen & Company edition. Translated from “On the Electrodynamics of Moving Bodies,” by Albert Einstein.

[[xv]]       Anon., “Einstein Expounds His New Theory: It Discards Absolute Time and Space, Recognizing Them Only as Related to Moving Systems; Improves on Newton; Whose Approximations Hold for Most Motions, but Not Those of the Highest Velocity; Inspired as Newton Was; But by the Fall of a Man from a Roof Instead of the Fall of an Apple,” New York Times, December 3, 1919.

[[xvi]]      van Delft, Dirk, “Albert Einstein in Leiden,” Physics Today, April 2006, pp. 57-62. See: https://www.lorentz.leidenuniv.nl/history/einstein/vol59no4p57_62.pdf. Note, Sidelights in Relativity,

[[xvii]]      Einstein, Albert, The Collected Papers of Albert Einstein, Edited by Michael Janssen, Robert Schulmann, József Illy, Christoph Lehner, and Diana Kormos Buchwald, Volume 7: The Berlin Years: Writings, 1918-1921, Princeton: Princeton University Press, 2002, p. 105. See: https://einsteinpapers.press.princeton.edu/vol7-doc/153.

[[xviii]]     “Twin paradox employing a rocket following an acceleration profile in terms of coordinate time T and by setting c=1: Phase 1 (a=0.6, T=2); Phase 2 (a=0, T=2); Phase 3-4 (a=-0.6, 2T=4); Phase 5 (a=0, T=2); Phase 6 (a=0.6, T=2). The twins meet at T=12 and τ=9.33. The blue [unprimed] numbers indicate the coordinate time T in the inertial frame of the stay-at-home-twin, the red [primed] numbers the proper time τ of the rocket-twin, and "a" is the proper acceleration. The thin red lines represent lines of simultaneity in terms of the different momentary inertial frames of the rocket-twin. The points marked by blue [primed] numbers 2, 4, 8 and 10 indicate the times when the acceleration changes direction.” After: https://en.wikipedia.org/wiki/Twin_paradox#/media/File:TwinParadoxProperAcceleration.svg

[[xix]]      Einstein, Albert, Sidelights on Relativity, New York: Dover Publications, 1983, p. 23. Reprinting a lecture: Ether and the Theory of Relativity, An Address delivered on May 5, 1920, University of Leyden. Note the more typical spelling is “Leiden,” and although originally scheduled for May 5, difficulties in securing the visiting professorship delayed the inaugural lecture until October 27, 1920 (see van Delft’s account).

[[xx]]       Einstein, Albert, Leopold Infeld, The Evolution of Physics, Cambridge: Cambridge University Press, 1938, pp. 183-184.

[[xxi]]      Holton, Gerald, “Origins of Relativity,” Am. J. Phys., Oct. i960, pp. 627-636.