5.2.3 The Search for Vulcan

And What Was Going On With Uranus?

Uranus was not where it was supposed to be, according to Newton’s theory. William Herschel (1738–1822) identified Uranus as a planet in 1781, however the seventh planet had been captured in earlier star charts by astronomers who failed to recognize it as a planet. Those earlier positions were difficult to reconcile with the planet’s location in the decades following its discovery. Even relying only upon the most modern and accurate measurements, Uranus kept getting ahead of schedule, moving a bit faster than it ought to, until about 1822 when the situation changed, and Uranus started moving a bit slower than expected [[i]].

French astronomer, Urbain Le Verrier (1811–1877), surmised the solution was a hitherto unknown eighth planet. In 1846, he calculated the current position of his unknown planet. Having trouble persuading a French astronomer to take a look, Le Verrier sent a note to German astronomer Johann Gottfried Galle (1812–1910). Having access to excellent and recently updated star charts, Galle and his assistant discovered Neptune within one degree of Le Verrier’s predicted position in less than an hour. Le Verrier had “discovered the planet with the point of his pen” in the words of François Arago (1786–1853), director of the Paris Observatory and Le Verrier’s supervisor and mentor [[ii]].

Le Verrier’s 1846 achievement was soon clouded by Astronomer Royal, George Biddell Airy (1801–1892), who we last met in Chapter 3 contemptuously dismissing Faraday’s field lines. Airy’s story was that John Couch Adams (1819–1892), an English mathematician and astronomer, had made a similar prediction even earlier than Le Verrier, and astronomer James Challis (1803–1882) had been looking for the eighth planet in almost the same location Le Verrier had predicted. Airy argued that Adams and Le Verrier deserved equal credit for the discovery [[iii]].

In more recent times, scholars went looking to document the story, only to be told the file was “unavailable.” Missing from the Royal Greenwich Observatory for thirty years, a staff member took the file with him to a Chilean observatory. The historical records only reappeared when colleagues in Chile searched through his personal effects after his death in 1998 [[iv]].

Figure 5.17: Comparison of Le Verrier’s and J.C. Adams’ claimed predictions of a hypothetical eighth planet with Neptune’s actual position. After [[v]].

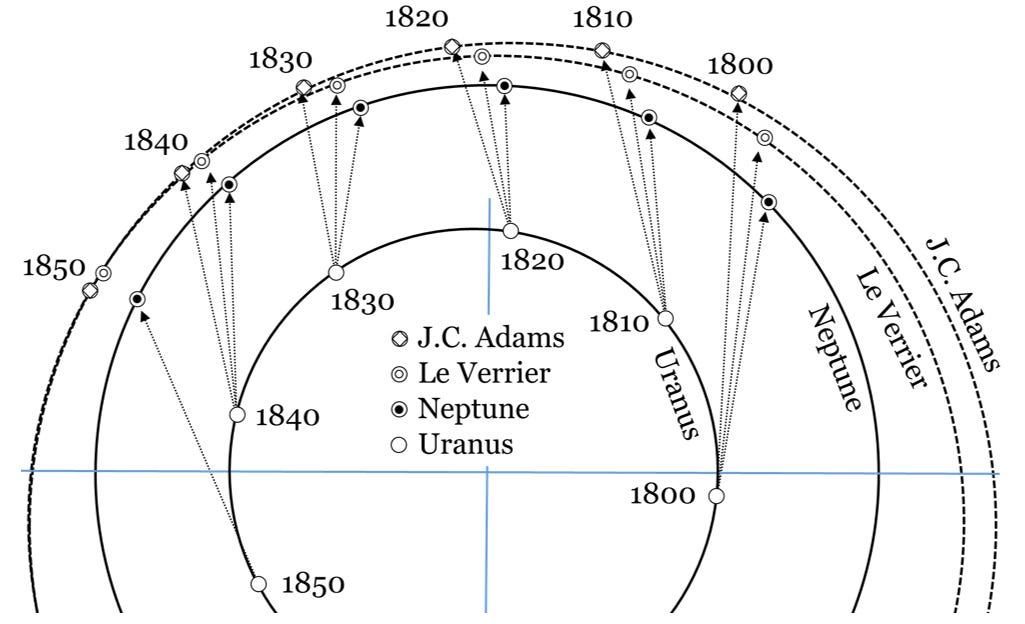
The truth appears to be that Adams did send Airy a note with predictions on an eighth planet, but when Airy requested more details, Adams didn’t answer, and both let the matter drop until Airy learned of Le Verrier’s prediction the following year. Noting the similarity to Adams’ prediction, Airy tasked Challis with the search. The close agreement of Adams’ prediction with Le Verrier’s (shown in Fig. 5.17) was only refined after the discovery; Adams’ search parameters were much wider. The search that took Galle merely an hour once he got started consumed months of Challis’ time. Lacking detailed star charts, Challis painstakingly mapped about 3000 stars in the broad region Adams targeted. Challis then returned a couple of weeks later to see if any stars he charted had moved. In fact, Challis’ records showed he had observed Neptune twice, but he had not completed his comparisons to identify his observation as a planet before Galle’s discovery [[vi]].

According to a recent article on the controversy…

“…we can affirm that Adams does not deserve equal credit with Le Verrier for the discovery of Neptune. That credit belongs only to the person who succeeded both in predicting the planet’s place and in convincing astronomers to search for it. The achievement was Le Verrier’s alone [[vii]].

Figure 5.18: Urbain Le Verrier (1811–1877) [[viii]], left, and perihelion advance of an elliptical orbit with the sun at one focal point, center. Both orbit eccentricity (0.6) and the magnitude of the advance (20^o/orbit) are grossly exaggerated. Mercury’s orbital eccentricity is ~0.21, and its total precession advances 5600”/century (1.56^o/century), during which time Mercury will have made 241 orbits at 88 Earth days/orbit. Note there are sixty arcseconds per arcminute (60”/’) and 60 arcminutes per degree (60’/deg). Mercury and any other planets inside Earth’s orbit, may be tracked by observing their occasional solar transits. Here, Mercury appears as a small black dot as it transits the sun [[ix]], right.

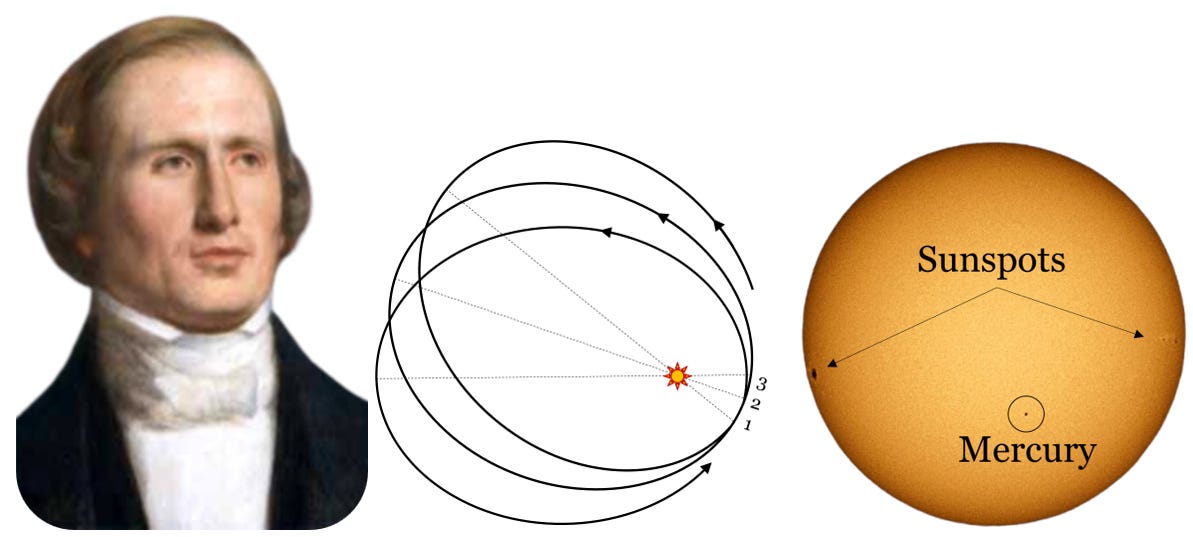
With Neptune discovered, Le Verrier returned to the problem he’d been working on before the distraction. Astronomers had noted an anomalous perihelion advance of the planet Mercury. The discovery of Neptune validated both Newton’s theory of universal gravitation and the approach of inferring the existence of hitherto unknown planets from perturbations in the orbits of known planets. Mercury’s perihelion (closest approach to the sun) advances at 5600 arcseconds (about 1.56 deg) every century. Precession of Mercury’s equinox – tidal forces acting upon the unequal quadrupole distribution of Mercury’s mass – accounts for 5025 arcseconds/century. Perturbations from other planets account for 532 arcseconds/century. That leaves a residue of 43 arcseconds/century unaccounted for [[x]].

An accuracy of 99% wasn’t enough for a perfectionist like Le Verrier. Newton’s clockwork universe had to operate precisely on time. How accurate was the Newtonian model? Writing in 1852, Scottish astronomer Robert Grant (1814–1892) declared:

The moon in the present day is about two hours later in coming to the meridian than she would have been if she had retained the same mean motion as in the time of the earliest Chaldean observations. It is a wonderful fact in the history of science that those rude notes of the priests of Babylon should escape the ruin of successive empires, and, finally, after the lapse of nearly 3,000 years, should become subservient in establishing a phenomenon so refined and complicated a character as the inequality we have just been considering [[xi]].

Accurate enough that subtle perturbations slowing the moon a couple of hours over 3,000 years were being readily calculated.

Some unknown and unaccounted for factor was perturbing the orbit of Mercury, and Le Verrier’s experience with Neptune gave him a good idea what it had to be. Somewhere lost in the glare of the Sun inside the orbit of Mercury there must be an unknown planet responsible for the perturbations. That was the inevitable conclusion of then well-settled science. This unknown planet, dubbed “Vulcan” (because of its toasty orbit close to the Sun), could easily have been overlooked due to the difficulty of spotting such a small planet in close proximity to the Sun [[xii]].

Vulcan was literally “dark matter.” Astronomers searched for Vulcan by observing the solar disk for the transit of a tiny unknown planet blocking a small portion of the Sun’s light. As the fruitless search continued, astronomers placed tighter and tighter limits on the size of the supposed planet Vulcan until it became obvious no such planet of the size necessary to perturb Mercury’s orbit could possibly exist [[xiii]].

Others sought a different explanation. In 1898, Paul Gerber (1854–1909), a German high school teacher living in Poland, calculated the perihelion advance assuming gravity propagated at the speed of light [[xiv]], through a somewhat questionable method [[xv]]. His result did not attract much attention at the time.

Special relativity applies only to inertial reference systems – to systems and observers moving with constant velocities. A more general theory of relativity was needed to encompass accelerating reference frames and gravitation. The new theory would rely upon an important clue.

Next time: 5.2.4 The Equivalence Principle: Everything Falls Together

Enjoyed the article, but maybe not quite enough to spring for a paid subscription?
Then click on the button below to buy me a coffee. Thanks!

Full Table of Contents [click here]

Follow Online:

You may follow me online in other places as well:

• Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞

• Gab: @aetherczar

• Twitter: @aetherczar

• Amazon: Hans G. Schantz

• ResearchGate

• Google Scholar

• ORCID

---

References

---

[[i]] Krajnović, Davor, “The contrivance of Neptune,” Astronomy & Geophysics, vol. 57 no. 5, October 2016, pp. 5.28–5.34. doi:10.1093/astrogeo/atw183

[[ii]] Danjon, A., “Le centenaire de la découverte de Neptune,” Ciel et Terre, Vol. 62, 1946, p. 369.

[[iii]] Royal Astronomical Society, vol. VII, no. 9, November 13, 1846.

[[iv]] Anonymous, “British Neptune-Disaster File Recovered NOAO-DIO Preservation Project Succeeds Long-Hidden RGO File on 1846 Planet-Chase: Safe At Last Adams’ Final Prediction Missed by Over Ten Degrees Britain’s “Discoverer”: Perfect Simp or Conniving Babe?” DIO: The International Journal of Scientific History, vol. 9, no. 1, June 1999, pp. 3-25. See: http://www.dioi.org/vols/w91.pdf

[[v]] After Danjon, A., “Le centenaire de la découverte de Neptune,” Ciel et Terre, Vol. 62, 1946, p. 369. See: https://articles.adsabs.harvard.edu//full/1946C%26T....62..369D/0000380.000.html

[[vi]] Sheehan, William, Nicholas Kollerstrom, Craig B. Waff, “The Case of the Pilfered Planet,” Scientific American, vol. 291 no. 6, December 2004, pp. 92–99. doi:10.1038/scientificamerican1204-92

[[vii]] Sheehan, William, Nicholas Kollerstrom, Craig B. Waff, “The Case of the Pilfered Planet,” Scientific American, vol. 291 no. 6, December 2004, pp. 92–99. doi:10.1038/scientificamerican1204-92

[[viii]] Painting of Le Verrier from the records of Paris Observatory. See: https://en.wikipedia.org/wiki/Urbain_Le_Verrier#/media/File:Le_Verrier_colored.jpg

[[ix]] Courtesy, Wikipedia. “The Historical Transit of Mercury on November 8, 2006. Please note that sunspot #923, which is just below the equator at the left-hand side, is much bigger than Mercury is. You could also see two more sunspots at the right-hand side at the equator. You could see Mercury as a small black dot in the lower middle of the solar disk. Limb darkening is clearly seen at the image. The picture was taken with a white filter and prime focus. The grainyness in the Sun is called granulation.” See: https://en.wikipedia.org/wiki/File:Mercury_transit_2.jpg

[[x]] Bowler, M.G., Gravitation and Relativity, Oxford: Pergammon Press, 1976, p. 98.

[[xi]] Grant, Robert, History of physical astronomy from the earliest ages to the middle of the nineteenth century, London: HENRY G. BOHN, YORK STREET, COVENT GARDEN, 1852, p. 63-64. See: https://archive.org/details/historyofphysica00granrich/page/62/mode/2up

[[xii]] Baum, Richard, and William Sheehan, The Ghost in Newton’s Clockwork Universe: In Search of Planet Vulcan, Springer Science, 1997.

[[xiii]] Levenson, Thomas, The Hunt for Vulcan: How Albert Einstein Destroyed a Planet and Deciphered the Universe, New York: Random House, 2015.

[[xiv]] Beckmann, Petr, Einstein Plus Two, Boulder, CO: Golem Press, 1987, pp. 170-175. The speed of gravity is a fascinating concept. Laplace argued gravity had to be many millions of times faster than the speed of light. Heaviside claimed to demonstrate that wasn’t so. Also, If the Earth were attracted to the apparent instead of the actual position of the sun, it would spiral outward – which obviously doesn’t happen. I worked through Gerber’s calculation in graduate school and concluded he made some erroneous simplifications. So, I accept Pauli’s argument that Gerber’s calculation was based on “false deductions.”

[[xv]] Pauli, Wolfgang, Theory of Relativity, New York: Dover, 1981, p. 169. A reprint of the 1958 edition by Pergamon Press; originally published in German as Relativitätstheorie, 1921.