5.2.4 The Equivalence Principle

Everything Falls Together

Aristotelian physics holds that all bodies move according to their nature and their natural place. Stones fall to the earth; fire rises to the sky. Thus, Aristotle’s adherents assumed heavy bodies fell faster than lighter bodies. This was disputed as early as the sixth century by the Byzantine Church Father, John Philoponus (~490–~570), who noted, we presume from experiment, “that two unequal weights dropped from a given height strike the ground at almost the same time” [[ii], [iii]].

If that sounds familiar, you may be thinking of the famous demonstration Galileo (1564–1642) conducted at the Leaning Tower of Pisa. There are some subtleties omitted from the usual popular account of the event, however. In particular, the experiment was done by Simon Stevin (1548–1620) and Jan Cornets de Groot (1554–1640), not by Galileo, and they conducted the experiment from the Niewe Kerk [New Church] in Delft, the Netherlands, not from the Leaning Tower of Pisa [[iv]].

Figure 5.19: The conventional description of Galileo’s experiment [[i]].

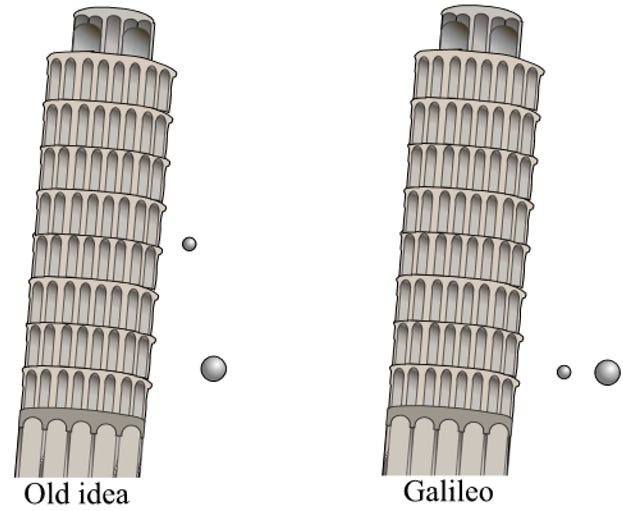
It is possible that Galileo did conduct the fabled experiments from the Tower of Pisa, however, the only documentation we have of this comes from one report in a biography published by his student, Vincenzo Viviani (1622–1703), published in 1654 [[v]]. Galileo did, though, explain the paradoxes involved in the assumption heavier bodies fall faster in his 1638 work, Dialogues Concerning Two New Sciences [[vi]], and his pendulum experiments suggested that different materials swung at the same rate.

Figure 5.20: The Reverend Marin Mersenne (1588–1648) [[vii]], top left, Christiaan Huygens (1629–1695) [[viii]], top right, Huygens’s 1657 spring driven pendulum clock, bottom left, and a copy of Huygens’s Horologium Oscillatorium (1673) open to the page describing the clock [[ix]].

The inertial mass that determines the ratio of force to acceleration is the same mass as the gravitational mass determines gravitational interactions. In other words, all bodies of every kind fall the same way. This observation, the “equivalence principle,” suggests gravitation may be indistinguishable from acceleration.

Father Marin Mersenne (1588–1648) built on Galileo’s foundation to perfect the theory of pendulum motion, and Christiaan Huygens (1629–1695) (about whom we will learn much more when our attention turns to optics in Chapter 7) designed the first spring driven pendulum clock which was built in 1657 [[x]].

Precise time is essential to the determination of longitude, in particular, and navigation in general. Creating a version of Huygens’s clock that could reliably keep time on board a ship was a vexing problem that required an additional century to untangle. That story is told elsewhere [[xi]].

Isaac Newton (1642–1727), Friedrich Wilhelm Bessel (1784–1846), and others refined Galileo’s pendulum experiment, as perfected by Mersenne and Huygens, to achieve tighter limits on the equivalence principle [[xii], [xiii]]. By comparing the periods of pendulums hung with the same length but different materials in the bob, they further confirmed that the motion of any freely falling object is independent of its mass, composition, or structure, provided it is only influenced by gravity.

The Hungarian physicist, Baron Loránd Eötvös de Vásárosnamény (1848–1919), took the precision of these experiments to the next level in 1891, by extending upon the torsion balance concept Henry Cavendish (1848–1919) and others had used to measure subtle gravitational forces [[xiv]]. By mounting a mirror to the suspending wire and shining a collimated beam of light at the mirror, Eötvös greatly amplified even small deflections, creating a remarkably sensitive torsion balance. Any difference in the gravitational mass with respect to the inertial mass would introduce a noticeable twist in the torsion balance over the course of a day, due to the varying gravitational attraction of the sun. Eötvös was able to demonstrate the equivalence of gravitational and inertial mass to a precision of about 5 × 10^-8 for a wide variety of materials.

Figure 5.21: Simple Eötvös torsion balance [[xix]], left, double torsion balance [[xx]], center, Baron Loránd Eötvös de Vásárosnamény (1848–1919) [[xxi]], right.

An Eötvös torsion balance with one weight suspended lower than the other also proved a very sensitive instrument for detecting local gravity gradients. They were able to identify both buried ore deposits much more dense than surrounding rock, or lower density salt domes (associated with oil deposits) [[xv], [xvi]].

Robert H. Dicke (1916–1997) and his collaborators improved further upon Eötvös’s technique, achieving a null result to a precision of < 1.3 × 10^-11 in 1964 [[xvii]], and in 1971, Vladimir Borisovich Braginsky (1931–2016) refined the precision further to < 9 × 10^-13 [[xviii]].

Figure 5.22: Summary of select equivalence measurements.

Braginsky used elements with different ratios of protons (p⁺), electrons (e^-), and neutrons (n⁰). He compared platinum (¹⁹⁵Pt with 78 p⁺, 78 e^-, and 117 n⁰) to aluminum (²⁷Al with 13 p⁺ and 14 n⁰). For instance, Pt is 65% n⁰ while Al is 52% n⁰. His result thus confirmed the equivalence of inertial to gravitation mass for neutrons versus protons, and for electrons versus nucleons. Similar arguments can be made for nuclear, atomic, and even gravitational binding energies, the ratios of which also differ between the two elements [[xxii]]. More recent experiments have demonstrated equivalence for matter versus antimatter [[xxiii], [xxiv], [xxv]].

At the end of the Apollo 15 moon walk in 1971, Commander David Scott repeated the experiment less precisely, but more dramatically, by dropping a hammer and a falcon feather simultaneously in the lunar vacuum to demonstrate they both fell at the same rate [[xxvii]].

Figure 5.23: David Scott’s 1971 test of the equivalence principle on the moon. Courtesy, Greta Schantz [[xxvi]].

These more refined demonstrations and experimental tests of the Equivalence Principle came too late to influence the initial development of General Relativity, however. Arguing from the results of Eötvös, in 1907 Planck reasoned that because all energy has inertial properties, it must gravitate as well. A few months later, Einstein authored a paper noting the equivalence of inertial and gravitational acceleration, introducing what he would later dub the Principle of Equivalence [[xxviii]]. Also in 1907, Einstein wrote to a friend that he was working on a relativistic theory of gravity by which he hoped to explain the anomalous perihelion precession of Mercury [[xxix]]. Despite these preliminary indications, Einstein didn’t begin working in earnest on gravitation until 1911 [[xxx]], when he first suggested that perhaps light could be bent by the gravitational attraction of the sun [[xxxi]].

Next time: 5.2.5 Can Gravity Bend Light? Making a Scientific Superstar

Enjoyed the article, but maybe not quite enough to spring for a paid subscription?
Then click on the button below to buy me a coffee. Thanks!

Full Table of Contents [click here]

Follow Online:

You may follow me online in other places as well:

• Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞

• Gab: @aetherczar

• Twitter: @aetherczar

• Amazon: Hans G. Schantz

• ResearchGate

• Google Scholar

• ORCID

---

References

---

[[i]] Pisa experiment by Galileo Galilei. Drawn by Theresa Knott. See: https://commons.wikimedia.org/wiki/File:Pisa_experiment.png

[[ii]] Wolff,Michael, “Philoponus and the Rise of Preclassical Dynamics,” collected in Philoponus and the Rejection of Aristotelian Science, Richard Sorabji, ed., Ithaca, New York: Cornell University Press, 1987, p. 94. “It is just this assumption that Philoponus tries to justify by the observation ‘that two unequal weights dropped from a given height strike the ground at almost the same time’ (zn Phys 683,16-25). From this observation Philoponus does not derive what Galileo assumed to be true, namely that bodies of different absolute weight fall equally fast in the same medium (or in the void). Instead Philoponus, like Aristotle, thinks that velocity increases with heaviness. ‘The more heavy bodies are combined, the greater will be the speed at which they move’ (in Phys 420,13f). And ‘the same space will consequently be traversed by the heavier body in a shorter time and by the lighter body in a longer time, even though the space be void’ (in Phys 679,20-21). Philoponus even denies the additivity of weights, saying that the weight of two bodies combined is greater than the sum of the weights of the individual bodies (in Phys 420,8ff). For this reason, his observation explicitly excludes consideration of weights which differ considerably from each other (in Phys 683,21f). If the difference is small, the (merely resistant) medium will almost entirely compensate for the difference of velocities resulting from the difference of weights. Philoponus’ observation, as he interprets it, confirms precisely this compensation.”

[[iii]] Sorabji, Richard, “John Philoponus,” collected in Philoponus and the Rejection of Aristotelian Science, Richard Sorabji, ed., Ithaca, New York: Cornell University Press, 1987, p. 14. “We must not exaggerate Philoponus’ contribution. It has been pointed out’ that his positive account of velocity in a vacuum falls short of Galileo’s on at least two counts. First, he thinks, wrongly, that there will be a marginal difference in speed of fall according to the weight of the body. For this he refers to experiments with dropping weights such as were subsequently credited to Galileo. Secondly, in talking of weight, he is thinking of gross weight, not of Galileo’s concept of specific weight which takes into account the volume of a body and permits a direct mathematical comparison between the falling body and the medium through which it falls. None the less, it must be said that at the time of the de Motu, Galileo himself had not yet reached the idea of the equal velocity of freely falling bodies in a vacuum.”

[[iv]] Plaice, John, “Galileo Galilei's and Simon Stevin's Tower Experiments,” Fiat Lux, January 21, 2024. See:

Galileo Galilei's and Simon Stevin's Tower Experiments

[[v]] Plaice, John, “Galileo Galilei's and Simon Stevin's Tower Experiments,” Fiat Lux, January 21, 2024. See:

Galileo Galilei's and Simon Stevin's Tower Experiments

[[vi]] Plaice, John, “Galileo Galilei on Falling Bodies,” Fiat Lux, January 22, 2024. See:

Galileo Galilei on Falling Bodies

[[vii]] Marin Mersenne. See: https://en.wikipedia.org/wiki/Marin_Mersenne#/media/File:Marin_mersenne.jpg Credit: http://www.york.ac.uk/depts/maths/histstat/people/ Abb.4 from H Loeffel, Blaise Pascal, Basel: Birkhäuser 1987. DSB 9, 316-322.

[[viii]] Huygens by Caspar Netscher (1671), Museum Boerhaave, Leiden. See: https://en.wikipedia.org/wiki/Christiaan_Huygens#/media/File:Christiaan_Huygens-painting.jpeg

[[ix]] Spring-driven pendulum clock, designed by Huygens and built by Salomon Coster (1657), with a copy of the Horologium Oscillatorium (1673), at Museum Boerhaave, Leiden. Credit Rob Koopman (Flickr profile) - https://www.flickr.com/photos/koopmanrob/3775343287/sizes/o/; see: https://en.wikipedia.org/wiki/Christiaan_Huygens#/media/File:Christiaan_Huygens_Clock_and_Horologii_Oscillatorii.jpg “One of the first pendulum clocks designed by Christiaan Huygens, and his treatise on the pendulum, Horologium Oscillatorium published in 1673, on display in Museum Boerhaave in Leiden, Netherlands. This may be Huygens's second pendulum clock, which was also finished in 1673 and is shown on the open page of the book. In it, Huygens demonstrated how to make the swing of the pendulum isochronous using "cycloidal" cheeks of metal (shown on page) to confine the suspension cord and give the pendulum a cycloidal trajectory. Huygens claimed an accuracy of 10 seconds per day.”

[[x]] Poynting, John Henry, and Joseph John Thomson, A Textbook of Physics, vol. 1, 4^th ed., London: Charles Griffin and Company, Limited, 1907, pp. 8-9.

[[xi]] Sobel, Dava, Longitude: The True Story of a Lone Genius Who Solved the Greatest Scientific Problem of His Time, New York: Walker and Company, 1995. See: https://amzn.to/3CKC3Ji.

[[xii]] Newton, Isaac, Principia, Book II, Section VI, Proposition XXIV, pp. 303-304. “And hence appears a method both of comparing bodies one among another, as to the quantity of matter in each ; and of comparing the weights of the same body in different places, to know the variation of its gravity. And by experiments made with the greatest accuracy, I have always found the quantity of matter in bodies to be proportional to their weight.”

[[xiii]] Ciufolini, Ignazio, and John Archibald Wheeler, Gravitation and Inertia, Princeton: Princeton University Press, 1995, p. 91.

[[xiv]] Szabó, Zoltán, “The history of the 125 year old Eötvös torsion balance,” Acta Geodaetica et Geophysica, 24 July 2015. Doi:10.1007/s40328-015-0126-4

[[xv]] E.R.F., “The ‘Eötvös’ Torsion Balance,” Nature, vol. 118, no. 18 September 1926, p. 406. Doi: 10.1038/118406a0.

[[xvi]] Howarth, Richard, “Gravity Surveying in Early Geophysics. II. From Mountains to Salt Domes,” Earth Sciences History, 26, 2007, pp. 229-261.

[[xvii]] P.G Roll; R Krotkov; R.H Dicke. (1964). The equivalence of inertial and passive gravitational mass. Annals of Physics, 26(3), 442–517. doi:10.1016/0003-4916(64)90259-3

[[xviii]] Bowler, M.G., Gravitation and Relativity, New York: Pergamon Press, 1976, pp. 27-35.

[[xix]] Eötvös, Dr. Baron Roland, “Die Niveauflächen und die Gradienten der Schwerkraft Am Balatonsee,” Budapest, 1908, p. 24. See: https://real-eod.mtak.hu/7919/1/Tmtan_Qu_391_001036869.pdf

[[xx]] Wilson, John H., “Geophysical Prospecting: Part Three – Torsion Balances,” The Colorado School of Mines Magazine, Vol. XVIII, no. 6, October 1928, pp. 17-23. See: https://books.google.com/books?id=schkPR9aqW0C&newbks=1&newbks_redir=0&dq=eotvos%20torsion%20balance%20illustration&pg=RA10-PA17#v=onepage&q=eotvos%20torsion%20balance%20illustration&f=false

[[xxi]] Portrait by Gustav Morelli (1889) of Dr. Baron Roland Eötvös. See https://en.wikipedia.org/wiki/Lor%c3%a1nd_E%c3%b6tv%c3%b6s#/media/File:E%C3%B6tv%C3%B6s_Lor%C3%A1nd_Morelli.jpg

[[xxii]] Bowler, M.G., Gravitation and Relativity, New York: Pergamon Press, 1976, pp. 27-35.

[[xxiii]] Nieto, Michael Martin and T. Goldman, “The arguments against ‘antigravity’ and the gravitational acceleration of antimatter,” Physics Reports 205, no. 5, 1991, pp. 221–281. doi:10.1016/0370-1573(91)90138-c

[[xxiv]] Borchert, M.J., Devlin, J.A., Erlewein, S.R. et al., “A 16-parts-per-trillion measurement of the antiproton-to-proton charge–mass ratio,” Nature, vol. 601, 5 January, 2022, pp. 53–57. doi: 10.1038/s41586-021-04203-w

[[xxv]] Speake, Clive, C.M. Will, “Tests of the weak equivalence principle,”.Classical and Quantum Gravity, vol. 29, no. 18, September 2012, p. 1. doi: 10.1088/0264-9381/29/18/180301

[[xxvi]] Courtesy, Greta Schantz.

[[xxvii]] Williams, David R., “The Apollo 15 Hammer-Feather Drop,” 31 March, 2023, See: https://nssdc.gsfc.nasa.gov/planetary/lunar/apollo_15_feather_drop.html

[[xxviii]] Whittaker, Edmund, A History of the Theories of Æther and Electricity, vol. 2, New Tork: Harper and Brothers, 1960, see Chapter V, pp. 151-152. Originally published 1953.

[[xxix]] Jungnickel, Christa, and Russell McCormmach, Intellectual Mastery of Nature: Theoretical Physics from Ohm to Einstein Volume 2: The Now Mighty Theoretical Physics 1870-1925, Chicago: University of Chicago Press, 1986, p. 324.

[[xxx]] Pais, Abraham, ‘Subtle is the Lord…’ The Science and Life of Albert Einstein, Oxford: Oxford University Press, 1982, p. 187.

[[xxxi]] Jungnickel, Christa, and Russell McCormmach, Intellectual Mastery of Nature: Theoretical Physics from Ohm to Einstein Volume 2: The Now Mighty Theoretical Physics 1870-1925, Chicago: University of Chicago Press, 1986, p. 324.