5.2.5 Can Gravity Bend Light?

The Creation of General Relativity

The notion that gravitation might bend light rays was not original to Einstein (as his detractors would soon point out). In his 1704 Opticks, Newton himself asked:

Do not Bodies act upon Light at a distance, and by their action bend its Rays; and is not this action (cæteris paribus) strongest at the least distance?

In 1783, English natural philosophers John Michell (1724–1793) and Henry Cavendish (1731–1810) corresponded about the possibility of using the deflection of light to determine the mass of stars and speculated that light might not escape from a sufficiently massive body [[iii], [iv]].

Figure 5.25: Johann Georg von Soldner (1776–1833) [[i]], left, and his 1801 diagram of a light ray bent by the sun [[ii]], right.

In 1801, Johann Georg von Soldner (1776–1833) used a Newtonian physics approach to calculate deflection of light by the sun [[v]].

Hopefully no one finds it problematic, that I treat a light ray almost as a ponderable body. That light rays possess all absolute properties of matter, can be seen at the phenomenon of aberration, which is only possible when light rays are really material. And furthermore, we cannot think of things that exist and act on our senses, without having the properties of matter [[vi]].

In the conventional telling of the story, Soldner used classical Newtonian methods to calculate a result for the angular deflection of light grazing the sun [[vii]], half the value that would ultimately be observed.

More recently, one researcher argued that “…contrary to what we read since about 100 years, he found the right value” [[viii]]. Others point out “[a] direct comparison of Soldner’s and Einstein’s works is obscured by a confluence of various factors of two, arising both from different conventions and from printing errors” [[ix]]. Elsewhere, “[t]he formula Solder derived is shown to be equivalent to the classical formula. The formula only looks different because he used a different concept to describe the strength of the gravitational field than we do today” [[x]]. Interested readers may pursue this further, but the conclusion is that a Newtonian or classical calculation predicts light would bend about 0.875” as it grazes the sun. Since there are 3600” per degree, this is a very subtle deflection, and Soldner correctly concluded that the result “has no perceptible influence in practice” [[xi]].

Einstein began his quest for a more general theory of relativity from two premises. His first starting point was his 1907 insight regarding the equivalence of inertial and gravitational acceleration. His second starting point was the Principle of General Covariance, the notion that the laws of physics must remain unchanged under arbitrary coordinate transformations – whether inertial or accelerating. In 1911, he suggested that gravity might affect the speed of light [[xii], [xiii]].

Figure 5.26: The eclipse of August 21, 1914 cut across a continent at war in a contemporary illustration [[xiv]].

A colleague in Prague put Einstein in touch with Erwin Finlay-Freundlich (1885–1964), a young German astronomer eager to put Einstein’s prediction to the test [[xv], [xvi]]. In his first attempt, Finlay-Freundlich travelled to Brazil for the October 10, 1912 eclipse, and was rained out. One astronomer reported, “We suffered an eclipse instead of observing one” [[xvii]]. Undaunted, Finlay-Freundlich traveled to Crimea to observe the eclipse of August 21, 1914. The outbreak of World War I led to the Russians interning Finlay-Freundlich as an enemy alien. That left the field open for a concurrent American expedition from Lick Observatory. Unfortunately, they were rained out and had to leave their equipment behind in Russia [[xviii], [xix]]. These misfortunes were ultimately good news for Einstein, whose initial erroneous calculation of light deflection by the sun was identical to the Newtonian prediction. The difficulties involved in successfully executing the eclipse observations were such that Freundlich ultimately participated in a total of six such expeditions while successfully capturing data only once [[xx]].

Figure 5.27: Marcel Grossmann (1878–1936) [[xxiii]], left, and Erwin Finlay-Freundlich (1885–1964) [[xxiv]], right.

Einstein left Prague and returned to Zürich where long-time friend, Marcel Grossmann (1878–1936), was now a professor of mathematics specializing in non-Euclidean geometry at the Federal Polytechnic Institute [[xxi]]. The friend whose notes allowed Einstein to skip class, now became his mathematical collaborator. In 1913, Einstein and Grossmann offered an initial “covariant” relativistic theory of gravity [[xxii]].

Einstein’s intuition was good, but the mathematical implementation had problems. Their theory suggested a curvature of time, but not space, and their theory violated conservation of energy [[xxv]]. Worse, the Einstein-Grossmann theory only predicted about half of the Mercury perihelion anomaly [[xxvi]].

Later that year, Max Planck (1858–1947) and Walther Nernst (1864–1941) traveled from Berlin to Zürich to convey an enticing offer: an invitation for Einstein to join the Prussian Academy of Sciences, become a professor at the University of Berlin, and Director of the (soon-to-be-founded) Kaiser Wilhelm Institute of Physics [[xxvii]]. Einstein accepted the offer.

The outbreak of World War I may have impacted attempts to observe the eclipse in the Crimea, but Einstein continued working on his theory. In November 1915, with the war raging on, he made his breakthrough – but he faced stiff competition to be first.

Einstein’s math professor, Hermann Minkowski (1864–1909), had left Zürich in 1902 for Göttingen, “the Valhalla of mathematicians. It was here that Gauss and his student Riemann had explored the non-Euclidean geometries of curved surfaces and multidimensional spaces, and here that young geniuses like David Hilbert were reinventing mathematics” [[xxviii]].

In 1900, David Hilbert (1862–1943) presented a list of twenty-three unsolved problems, many of which were influential in guiding mathematical development in the twentieth century [[xxix]].

Hilbert, best known for his axiomatic foundations of mathematics and his formalist viewpoint, knew the value of important problems. As his disciple and biographer Otto Blumenthal (1876-1944) put it: “Hilbert is the man of problems. He collects and solves existing problems; he poses new ones.” Indeed, it is just by the solution of concrete problems that mathematics will be developed; in the end, problem solving and theory building go hand in hand. That's why Hilbert risked offering a list of unsolved problems instead of presenting new methods or results, as was usually done at meetings. “He who seeks for methods without having a definite problem in mind seeks for the most part in vain,” Hilbert told his Paris audience [[xxx]].

Figure 5.28: David Hilbert (1862–1943) [[xxxi]], left, and Gustav Mie (1869–1957) [[xxxii]], right.

Hilbert would not only become Einstein’s greatest rival in the quest to create a general relativistic theory of gravity [[xxxiii]], but also led Göttingen to mathematical pre-eminence. Another mathematician explains:

Under Hilbert, Göttingen reached its peak as one of the great mathematical centres of the world. No one in recent years has surpassed his dual capacity, for seeing and overcoming the central difficulty of some major topic, and for propounding new problems of vital importance [[xxxiv]].

Einstein and Hilbert raced down to the wire. “Einstein presented his two papers ‘On general relativity theory’ to the Berlin Academy on November 11 and 25; Hilbert presented his first note on ‘The foundations of physics’ to the Royal Society of Science in Gottingen on November 20, 1915” [[xxxv]].

Einstein and Hilbert were in close correspondence, and the virtual simultaneity of their conclusions led to disputes over priority. Their approaches were profoundly different, however.

Hilbert worked mathematically, starting from a unified field theory of gravitation and electromagnetism proposed by the German physicist Gustav Mie (1868–1957) in 1912-1913 [[xxxvi]]. Hilbert derived the correct result from variational principles [[xxxvii]].

Einstein’s more roundabout method started with the correct intuition relating the curvature of space to the distribution of mass and energy but an incorrect mathematical representation from his earlier 1913 theory [[xxxviii]]. He ultimately came to the correct equation a few days after Hilbert [[xxxix]].

The two were initially acrimonious, as Einstein struggled to understand how Hilbert achieved the same result. He thought Hilbert had stolen his work. One of Einstein’s biographers noted:

While Hilbert claimed to understand Einstein’s work better than Einstein himself, Albert still didn’t understand Hilbert’s work at all. He found it obscure, even after Hilbert had coached him through it, and he complained to Ehrenfest that Hilbert had “pretensions of being a superman” [[xl]].

“The people in Gottingen sometimes strike me, not as if they want to help one formulate something clearly,” Einstein grumbled, “but as if they want only to show us physicists how much brighter they are than we” [[xli]]. Hilbert in return offered Einstein this ironic and backhanded compliment:

Do you know why Einstein said the most original and profound things about space and time in our generation? Because he had learned nothing at all about the philosophy and mathematics of time and space! [[xlii]].

Hilbert was clear on the priority dispute:

Every boy in the streets of Göttingen understands more about four-dimensional geometry than Einstein. Yet, Einstein did the work and not the mathematicians [[xliii]].

It is difficult to justify the argument that Einstein plagiarized a mathematical theory that he did not understand. As another physicist aptly put it:

Einstein and Hilbert had the moral strength and wisdom – after a month of intense competition, from which, in a final account, everybody (including science itself) profited – to avoid a lifelong priority dispute (something in which Leibniz and Newton failed). It would be a shame to subsequent generations of scientists and historians of science to try to undo their achievement [[xliv]].

Figure 5.29: Einstein-Hilbert Field Equation for General Relativity.

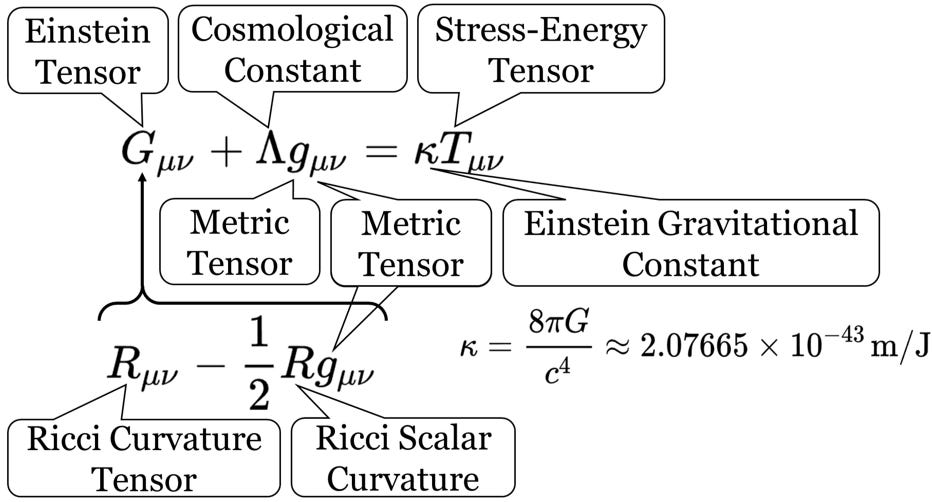
The Einstein-Hilbert theory itself may be expressed in a deceptively simple looking equation. Heaviside expressed Maxwell’s theory using vectors: mathematical constructs comprising three spatial quantities. Relativity deals in four-vectors: mathematical constructs comprising not only three spacial quantities but also time. Describing the interactions of those four-vectors with each other requires four-by-four tensors with sixteen components. The Einstein-Hilbert theory captured the curvature of space in a four-by-four tensor later called the “Einstein Tensor.” The Einstein Tensor may be broken down further into the difference of Ricci Curvature Tensor and half the Ricci Scalar Curvature times the Metric Tensor. The Metric Tensor captures the geometric properties of spacetime.

Interestingly, Einstein found he had to add a cosmological constant to counteract the attraction of gravity and ensure space remained static. As an expanding universe became the accepted hypothesis, Einstein told the physicist George Gamow (1904–1968) that the cosmological term was the “biggest blunder” he ever made in his life [[xlv]].

Finally, these spacetime parameters relate to the stress-energy tensor that captures the energy and momentum density, pressure and momentum flux.

Figure 5.30: Karl Schwarzschild (1873–1916) [[xlvi]], left, Johannes Droste (1886–1963) [[xlvii]], center, and Pierre Gassendi (1592–1655) [[xlviii]], right.

Einstein’s approximate solutions for the perihelion precession of Mercury and light deflection near the sun were quickly made rigorous by Karl Schwarzschild (1873–1916) [[xlix]], who died soon thereafter of an illness while serving on the Eastern Front [[l]]. A few months after that, Johannes Droste (1886–1963), a student of Hendrik Antoon Lorentz (1853–1928) at the University of Leiden, obtained the same solution [[li], [lii]].

But what is the physical meaning of General Relativity?

Pierre Gassendi (1592–1655), a French philosopher, Catholic priest, astronomer, and mathematician, rejected the notion of Descartes (1596–1650) that space was a plenum, and reintroduced the Greek atomists’ view that space was a void partially occupied by particles of matter and through which they move [[liii]].

Newton would adopt this view of a Euclidian space as the vacuum of the atomists, a “mere emptiness into which things could be put” [[liv]]. Edmund Whittaker (1873–1956) explains:

[Einstein] discarded Gassendi’s assumption that space was a uniform characterless vacuum, and postulated that it had a property of curvature, varying from point to point; and that just as (to make use of a rough analogy) a paramagnetic body when placed in a magnetic field tends to move from the weaker to the stronger places in the field, so a massive body in space might be pictured as moving from places of weak to places of strong curvature. The curvature, in fact, performs in General Relativity the same kind of function as the density and rigidity of the æther did in classical physics; but, unlike the æther properties, it does not come into conflict with the principle of relativity. In Einstein’s conception, space is no longer the stage on which the drama of physics is performed: it is itself one of the performers; for gravitation, which is a physical property, is entirely controlled by curvature, which is a geometrical property of space [[lv]].

Whittaker adds, “…gravitation represents a continual effort of the universe to straighten itself out: a statement so completely teleological that it would have delighted the hearts of schoolmen” [[lvi]].

John Archibald Wheeler (1911–2008) who, together with Russian physicist Yakov Zeldovich (1914–1987), [[lvii]] was one of the architects of the revival of general relativity in the 1950s, summed up General Relativity in a memorable quip:

Spacetime tells matter how to move;
matter tells spacetime how to curve [[lviii]].

Figure 5.31: John Archibald Wheeler (1911–2008) [[lix]] (Courtesy, Blackstone-Shelburne, New York, AIP Emilio Segrè Visual Archives, Wheeler Collection).

Einstein’s new 1915 theory predicted twice the deflection of light passing near the sun compared to his original 1911 prediction. An accurate measurement of this deflection during a solar eclipse, however, would await the end of World War I. The result of the observations would lead to Einstein becoming a scientific superstar. However, Einstein’s newly manufactured fame sparked lasting controversy.

Next time: 5.2.6 The Great Eclipse of 1919: Unequivocal? Or Confirmation Bias?

Enjoyed the article, but maybe not quite enough to spring for a paid subscription?
Then click on the button below to buy me a coffee. Thanks!

Full Table of Contents [click here]

Follow Online:

You may follow me online in other places as well:

• Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞

• Gab: @aetherczar

• Twitter: @aetherczar

• Amazon: Hans G. Schantz

• ResearchGate

• Google Scholar

• ORCID

---

References

---

[[i]] Johann Georg von Soldner 1776-1833. Erster Direktor der Sternwarte Bogenhausen, nach einem Porträt von 1816. See: https://en.wikipedia.org/wiki/Johann_Georg_von_Soldner#/media/File:Johann_Georg_Soldner_2.jpg

[[ii]] von Soldner, J.G., “Über die Ablenkungeines Lichtstrahls von seiner geradlinigen Bewegung, durch die Attraktion eines Weltkorpers, an welchem er nahe vorbei geht,” Berliner Astronomisches Jahrbuch, 1801, pp. 161-172. See: https://de.wikisource.org/wiki/Ueber_die_Ablenkung_eines_Lichtstrals_von_seiner_geradlinigen_Bewegung.

(PDF) Gravitational Deflection of Particles of Light by the Earth and by the Sun: A Reconstruction of the Calculations Done by Soldner in 1801. Available from: https://www.researchgate.net/publication/367745437_Gravitational_Deflection_of_Particles_of_Light_by_the_Earth_and_by_the_Sun_A_Reconstruction_of_the_Calculations_Done_by_Soldner_in_1801 [accessed Dec 05 2024].

[[iii]] Michell, John, “On the Means of discovering the Diſtance, Magnitude, &c. of the Fixed Stars, in conſequence of the Diminution of the Velocity of their Light, in caſe ſuch a Diminution ſhould be found to take place in any of them, and ſuch other Data should be procured from Obſervations, as would be farther neceſſary for that Purpose,” Philosophical Transactions of the Royal Society of London: Volume 74, p. 37, 1784, pp. 35-57. See p. 37.

“Let us now ſuppoſe the particles of light to be attracted in the ſame manner as all other bodies with which we are acquainted ; that is, by forces bearing the ſame proportion to their vis inertiæ, of which there can be no reasonable doubt, gravitation being, as far as we know, or have any reason to believe, an univerſal law of nature. Upon this ſuppoſition then, if any one of the fixed ſtars whoſe denſity was known by the above-mentioned means, ſhould be large enough ſenſibly to affect the velocity of the light iſſuing from it, we should have the means of knowing its real magnitude, &c.” See: https://books.google.com/books?id=Dk9FAAAAcAAJ&newbks=1&newbks_redir=0&dq=michell%20philosophical%20transaction%201784&pg=PA36#v=onepage&q=michell%20philosophical%20transaction%201784&f=false

[[iv]] Will, Clifford M., “Henry Cavendish, Johann von Soldner, and the deflection of light,” American Journal of Physics, vol. 56, no. 5, 1988, pp. 413–415. doi:10.1119/1.15622

[[v]] Whittaker, Edmund, A History of the Theories of Æther and Electricity, vol. 2, (New Tork: Harper and Brothers, 1960), p. 180. Originally published 1953.

[[vi]] von Soldner, J.G., “Über die Ablenkungeines Lichtstrahls von seiner geradlinigen Bewegung, durch die Attraktion eines Weltkorpers, an welchem er nahe vorbei geht,” Berliner Astronomisches Jahrbuch, 1801, pp. 161-172. See: https://de.wikisource.org/wiki/Ueber_die_Ablenkung_eines_Lichtstrals_von_seiner_geradlinigen_Bewegung.

(PDF) Gravitational Deflection of Particles of Light by the Earth and by the Sun: A Reconstruction of the Calculations Done by Soldner in 1801. Available from: https://www.researchgate.net/publication/367745437_Gravitational_Deflection_of_Particles_of_Light_by_the_Earth_and_by_the_Sun_A_Reconstruction_of_the_Calculations_Done_by_Soldner_in_1801 [accessed Dec 05 2024].

[[vii]] Will, Clifford, Was Einstein Right? Putting General Relativity to the Test, New York: Basic Books, Inc., 1986, pp. 66-67.

[[viii]] Mignonat, M., “Soldner Had Found in 1802 the Deflection of the Light by the Sun as the General Relativity Shows,” Journal of Modern Physics, 9, 2018, pp. 1545-1558. doi: 10.4236/jmp.2018.98095.

[[ix]] Sauer, Tilman, “Soldner, Einstein, Gravitational Light Deflection and Factors of Two,” Annalen der Physik, vol. 533, no. 8, June 2021. Doi: 10.1002/andp.202100203.

[[x]] Kampen, Frans, “Gravitational Deflection of Particles of Light by the Earth and by the Sun: A Reconstruction of the Calculations Done by Soldner in 1801,” International Journal of Astronomy and Astrophysics, vol. 12, 2022, pp. 147-165. Doi: 10.4236/ijaa.2022.121009.

[[xi]] von Soldner, J.G., Op. Cit.

[[xii]] Jungnickel, Christa, and Russell McCormmach, Intellectual Mastery of Nature: Theoretical Physics from Ohm to Einstein Volume 2: The Now Mighty Theoretical Physics 1870-1925, Chicago: University of Chicago Press, 1986, p. 325.

[[xiii]] Whittaker, Edmund, A History of the Theories of Æther and Electricity, vol. 2, New Tork: Harper and Brothers, 1960, p. 153. Originally published 1953.

[[xiv]] The Graphic, August 22, 1914. Cropped. See: https://www.theyearthatwaspodcast.com/s1e23-relativity-part1.

[[xv]] Jungnickel, Christa, and Russell McCormmach, Intellectual Mastery of Nature: Theoretical Physics from Ohm to Einstein Volume 2: The Now Mighty Theoretical Physics 1870-1925, Chicago: University of Chicago Press, 1986, p. 325.

[[xvi]] Kennefick, Daniel, No Shadow of a Doubt, Princeton, NJ: Princeton University Press, 2019, pp. 58-63.

[[xvii]] Rothman, Tony, Everything’s Relative: and Other Fables from Science and Technology, New York: John Wiley & Sons, 2003, p. 83.

[[xviii]] Campbell, W.W., H.D. Curtis, H.D. “The Lick Observatory-Crocker Eclipse Expedition to Brovarý, Russia,” Publications of the Astronomical Society of the Pacific, vol. 26 no. 156, 1914, pp. 225–237. Bibcode:1914PASP...26..225C. doi:10.1086/122351. See: https://archive.org/details/jstor-40710439.

[[xix]] Ohanian, Hans, Einstein’s Mistakes: The Human Failings of Genius, New York: W.W. Norton & Company, 2008, p. 211-212.

[[xx]] Kennefick, Daniel, No Shadow of a Doubt, Princeton, NJ: Princeton University Press, 2019, p. 335.

[[xxi]] Janssen, M., Renn, J., “History: Einstein was no lone genius,” Nature 527, 16 November, 2015, pp. 298–300. doi: 10.1038/527298a. Today, the Federal Polytechnic Institute in Zürich is called the “Eidgenössische Technische Hochschule Zürich” or ETH Zürich. Translated to English, “Swiss Federal Institute of Technology.”

[[xxii]] Jungnickel, Christa, and Russell McCormmach, Intellectual Mastery of Nature: Theoretical Physics from Ohm to Einstein Volume 2: The Now Mighty Theoretical Physics 1870-1925, Chicago: University of Chicago Press, 1986, p. 328-9.

[[xxiii]] ETH-BIB-Grossmann, Marcel (1878-1936)-Portrait-Portr 01239. See: https://en.wikipedia.org/wiki/Marcel_Grossmann#/media/File:ETH-BIB-Grossmann,_Marcel_(1878-1936)-Portrait-Portr_01239.tif_(cropped).jpg

[[xxiv]] See: https://en.wikipedia.org/wiki/Erwin_Finlay-Freundlich#/media/File:242_Erwin_Freundlich_Der_Astronom_Erwin_Freundlich_1.jpg .

[[xxv]] Ohanian, Hans, Einstein’s Mistakes: The Human Failings of Genius, New York: W.W. Norton & Company, 2008, pp. 194-198.

[[xxvi]] Ohanian, Hans, Einstein’s Mistakes: The Human Failings of Genius, New York: W.W. Norton & Company, 2008, pp. 199.

[[xxvii]] Ohanian, Hans, Einstein’s Mistakes: The Human Failings of Genius, New York: W.W. Norton & Company, 2008, pp. 199-201.

[[xxviii]] Overbye, Dennis, Einstein in Love: A Scientific Romance, New York: Viking, 2000, p. 158.

[[xxix]] Hilbert, David, “Mathematical Problems,” Bulletin of the American Mathematical Society, vol. 8, no. 10, 1902, pp. 437–479. doi:10.1090/S0002-9904-1902-00923-3.

[[xxx]] Thiele, Rüdiger, “Hilbert and his twenty-four problems,” in Mathematics and the historian's craft, New York: CMS Books Math./Ouvrages Math. SMC, 21, Springer, 2005, pp. 243-295.

[[xxxi]] Source possibly Reid, Constance (1970) Hilbert, Berlin, Heidelberg: Springer Berlin Heidelberg Imprint Springer, p. 230. See: https://en.wikipedia.org/wiki/File:Hilbert.jpg

[[xxxii]] Gustav Mie, source unknown. See: https://en.wikipedia.org/wiki/File:GustavMie.gif

[[xxxiii]] Todorov, Ivan T., “Einstein and Hilbert: The Creation of General Relativity,” arXiv:physics/0504179, April 25, 2005. See: https://arxiv.org/abs/physics/0504179

[[xxxiv]] Broadbent, Thomas Arthur Alan, “Review: Gesammelte Abhandlungen. II by David Hilbert; Gesammelte Abhandlungen. III by David Hilbert 1965,” The Mathematical Gazette, vol. 52, no. 379, February 1968, pp. 61-62. DOI: https://doi.org/10.2307/3614475 See: https://www.cambridge.org/core/journals/mathematical-gazette/article/abs/gesammelte-abhandlungen-by-david-hilbert-pp-xiv-539-ii-pp-viii-453-iii-pp-vii-435-rep-1965-chelsea-publishing-co-new-york/703AEABDDB2BF79E445D6CF3FB659063

[[xxxv]] Reid, Constance, Hilbert, New York: Springer Science, 1996, p. 142.

[[xxxvi]] Reid, Constance, Hilbert, New York: Springer Science, 1996, p. 142.

[[xxxvii]] Pais, Abraham, ‘Subtle is the Lord…’ The Science and Life of Albert Einstein, Oxford: Oxford University Press, 1982, pp. 257-258.

[[xxxviii]] Ohanian, Hans, Einstein’s Mistakes: The Human Failings of Genius, New York: W.W. Norton & Company, 2008, pp. 215-217.

[[xxxix]] Overbye, Dennis, Einstein in Love: A Scientific Romance, New York: Viking, 2000, pp. 290-293.

[[xl]] Overbye, Dennis, Einstein in Love: A Scientific Romance, New York: Viking, 2000, p. 295.

[[xli]] Reid, Constance, Hilbert, New York: Springer Science, 1996, p. 142.

[[xlii]] Reid, Constance, Hilbert, New York: Springer Science, 1996, p. 142.

[[xliii]] Reid, Constance, Hilbert, New York: Springer Science, 1996, p. 142.

[[xliv]] Todorov, Ivan T., “Einstein and Hilbert: The Creation of General Relativity,” arXiv:physics/0504179, April 25, 2005. See: https://arxiv.org/abs/physics/0504179

[[xlv]] Ohanian, Hans, Einstein’s Mistakes: The Human Failings of Genius, New York: W.W. Norton & Company, 2008, pp. 251.

[[xlvi]] Karl Schwarzschild, Deutscher Astronom und Physiker. See: https://commons.wikimedia.org/wiki/File:Karl_schwarzschild.portrait.jpg

[[xlvii]] Johannes Droste. 11 december 1925. Bibliotheek van de Hollandse Maatschappij der Wetenschappen, Haarlem. De huldiging van Professor Lorentz bij zijn gouden doctoraat (zijn promotie was in 1875 in Leiden op het proefschrift Over de theorie der terugkaatsing en breking van het licht) met 52 van de 54 dinergasten. Van links naar rechts (identificatie voltooid dankzij p. 67 in Frits Berends: Verhalen rond een foto. Lorentz’ gouden doctoraat: een huldiging zonder weerga, Koninklijke Hollandsche Maatschappij der Wetenschappen, Haarlem, z.j., waarvan de nummers worden vermeld bij de personen: https://www.khmw.nl/wp-content/uploads/verhalen_rond_een_foto.pdf. See: https://commons.wikimedia.org/wiki/File:Johannes_Droste._De_huldiging_van_Professor_Lorentz_bij_de_Hollandse_Maatschappij_der_Wetenschappen_in_1925_(cropped).jpg

[[xlviii]] Robert Nanteuil: portrait of Pierre Gassendi, Encyclopædia Britannica. See: https://www.britannica.com/topic/atomism/Modern-atomic-theory#/media/1/226651/253554

[[xlix]] Whittaker, Edmund, A History of the Theories of Æther and Electricity, vol. 2, New Tork: Harper and Brothers, 1960, see Chapter V, pp. 175-179. Originally published 1953.

[[l]] Pais, Abraham, ‘Subtle is the Lord…’ The Science and Life of Albert Einstein, Oxford: Oxford University Press, 1982, pp. 255.

[[li]] Rothman, Tony, “Editor’s Note: The Field of a Single Centre in Einstein's Theory of Gravitation, and the Motion of a Particle in That Field,” General Relativity and Gravitation, vol. 34, no. 9, pp. 1541–1543, doi:10.1023/a:1020795205829. See: https://www.lorentz.leidenuniv.nl/IL-publications/dissertations/biographies/Droste.pdf

[[lii]] Rothman, Tony, Everything’s Relative: and Other Fables from Science and Technology, New York: John Wiley & Sons, 2003, p. 81.

[[liii]] Whittaker, Edmund, Space and Spirit : theories of the Universe and the arguments for the existence of God, Hinsdale, Illinois: Henry Regenery Company: 1948, pp. 76-78. See: https://amzn.to/3ZFJWYh or https://archive.org/details/spacespirit0000unse/page/102/mode/2up?q=paramagnetic Note, there are some minor differences including in pagination in the 1946 English edition with respect to the 1948 U.S. edition.

[[liv]] Whittaker, Edmund, Space and Spirit : theories of the Universe and the arguments for the existence of God, Hinsdale, Illinois: Henry Regenery Company: 1948, p. 98. See: https://amzn.to/3ZFJWYh or https://archive.org/details/spacespirit0000unse/page/102/mode/2up?q=paramagnetic Note, there are some minor differences including in pagination in the 1946 English edition with respect to the 1948 U.S. edition.

[[lv]] Whittaker, Edmund, Space and Spirit : theories of the Universe and the arguments for the existence of God, Hinsdale, Illinois: Henry Regenery Company: 1948, pp. 99-100. See: https://amzn.to/3ZFJWYh or https://archive.org/details/spacespirit0000unse/page/102/mode/2up?q=paramagnetic Note, there are some minor differences including in pagination in the 1946 English edition with respect to the 1948 U.S. edition.

[[lvi]] Whittaker, Edmund, Space and Spirit : theories of the Universe and the arguments for the existence of God, Hinsdale, Illinois: Henry Regenery Company: 1948, p. 100. See: https://amzn.to/3ZFJWYh or https://archive.org/details/spacespirit0000unse/page/102/mode/2up?q=paramagnetic Note, there are some minor differences including in pagination in the 1946 English edition with respect to the 1948 U.S. edition.

[[lvii]] Collected in The Renaissance of General Relativity in Context, edited by Alexander S. Blum, Roberto Lalli, Jürgen Renn, Cham Switzerland: Springer Nature Switzerland, 2020, p. 287. See: https://amzn.to/4ge8L4B
“In the 1950s, two physicists—John Wheeler in the United States and later Yakov Zeldovich in the Soviet Union—emerged from their respective hydrogen bomb efforts and took up where Oppenheimer and his collaborators had left off in 1939, at the outburst of the war. Wheeler rediscovered Oppenheimer’s forgotten papers and was led to a systematic study of general relativity.”

[[lviii]] Wheeler, John Archibald, Geons, Black Holes, and Quantum Foam: A Life in Physics, New York: W.W. Norton & Company, 2000, p. 235. See: https://amzn.to/41zxwU4

[[lix]] Informal portrait of John Archibald Wheeler, 1911-2008. Credit Line: Blackstone-Shelburne, New York, courtesy of AIP Emilio Segrè Visual Archives, Wheeler Collection. Catalog ID: Wheeler John Archibald B23. Collection info:fedora/nbla:287972 See: https://repository.aip.org/islandora/object/nbla%3A312126