3.3 Potentials, Energy, & Fields
The Concepts Emerged From Crowdfunded & Self-Published Science
Potentials, energy, and fields: these concepts emerged from crowdfunded and self-published science. And despite Faraday’s success, many favored more mathematically elaborate approaches to electromagnetism. Read on!
Despite Faraday’s remarkable successes, there were those who preferred the mathematical descriptions of the action-at-a-distance school over Faraday’s qualitative conceptions. Sir George Biddell Airy (1801–1892), the astronomer royal of Great Britain and one-time Lucasian Professor of Mathematics argued, “I can hardly imagine anyone (who knows the agreement between observation and calculation based on action at a distance) to hesitate an instant between this simple and precise action on the one hand and anything so vague and varying as lines of force on the other” [[i]].

Meanwhile however, others had been working on a parallel approach. Joseph Louis Lagrange (1736–1813) introduced a mathematical function, “Σ,” whose derivative gives the gravitational force at any point in space [[ii]]. Pierre-Simon de Laplace (1749–1827) developed the function further, but denoted it, “V” [[iii]]. Siméon Denis Poisson (1781–1840) applied a similar function to electrostatics [[iv]]. At any given point in space, this function is the quantity of charge over its distance from the point summed up for every charge. This relationship was named the “electric potential” by a most unlikely physicist: a self-taught baker from Nottingham named George Green (1793–1841) [[v]].
Green’s mathematical skill prompted his father to send him to school for a year at age eight, but the following year he left school to work in the family business. When George was fourteen, his father apprenticed George to work for his mill manager. Little is known of George Green’s career until 1823 when at age thirty he joined a subscription library in Nottingham – effectively a gentlemen’s club (no, not THAT kind of gentlemen’s club!) that catered to the literary interests of its members.
Five years later, in 1828, Green crowdfunded the publication of a hundred copies of his work: An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism [[viii]]. Green’s discoveries included “Green’s Identities”–fundamental relations in vector calculus that relate the behavior in a volume to the behavior on the boundary of the volume. He also discovered “Green’s Functions,” which offer a way to calculate the physical behavior of a system by systematically adding contributions of its constituent parts to calculate the potential.
Disappointed at the lack of attention his erudite and innovative work received, he went back to milling. In 1830, the death of his father left Green with the income to pursue his studies full time. He wrote three more papers before enrolling as an undergraduate at Cambridge in 1833, at age forty. Becoming a Fellow at the college upon his graduation, he wrote a few additional papers, but died in 1841.
In his youth, Green took up with Jane, the daughter of the mill manager, despite his father’s disapproval. They were never married, and he officially never acknowledged his common-law wife, perhaps because only single men were eligible to become Cambridge Fellows. Although he provided generously for his seven children in his will, they suffered under the stigma of illegitimacy. Green’s son followed in his father’s footsteps, receiving a mathematics degree, but died by suicide. His last surviving daughter died in 1919, in the heavily mortgaged ruins of Green’s once prosperous estate. Helpful neighbors cleaned the place out, burning any rubbish and surviving letters or papers.

No photo or portrait of Green is known to exist, but Figure 3.9 shows the windmill he owned and managed, which was restored and became a monument to his memory in 1985. Figure 3.9 also presents a photo of William Thomson (1824–1907), later Lord Kelvin. As an undergraduate at Cambridge, Thomson worked out many fundamental results in what came to be called potential theory. He noticed a footnote mentioning Green’s essay. Intrigued, he set out to find a copy of Green’s monograph. At long last a friend gave him a couple copies in 1845 while Thompson was visiting Paris.
Thomson’s discovery of Green’s essay caused a great commotion in academic circles in Paris, because Green had anticipated, not only Thomson’s work, but also the results of such eminent mathematicians as Michel Chasles (1793–1880), Jacques Charles François Sturm (1803–1855), Joseph Liouville (1809–1882), and even Johann Carl Friedrich Gauss (1777–1855). In each case, Green had already worked out what they thought were their own original discoveries [[xi]].
The potential theory of Green and others provided the mathematical framework within which electromagnetism would be studied in the early nineteenth century.
In 1847, a young physician with an interest in physics, Hermann von Helmholtz (1821–1894), presented the first comprehensive theoretical treatment of conservation of energy to the Berlin Physical Society. Although well-received, Helmholtz’s epic paper, “On the Conservation of Force,” was rejected as “too speculative” to be published in the Annalen – the leading German physics journal of the day. He self-published his work as a pamphlet, instead. Helmholtz’s analysis also included a study of electrical energy, in which the energy was assumed to be associated with individual charges [[xiii], [xiv]]. In this theory, as two charge distributions interact, they exert forces on each other. In the application of these forces, one charge distribution loses energy while the other gains energy. From the action-at-a-distance perspective, energy vanishes in one place and instantaneously reappears in another.

A few years later, Thomson (Kelvin) came up with another way to calculate energy, one using fields instead of charges and potentials [[xv], [xvi]]. In Kelvin’s approach, electric energy is proportional to the square of the field intensity. The proportionality constant involves the electric permittivity – we’ll discuss that in a later section. Kelvin’s theory suggests that electric energy resides, not in charges, but rather in the surrounding space, making it easier to imagine that energy might be able to flow from one place to another. Figure 3.10 compares Kelvin’s approach to the Helmholtz approach.
In the early days of electromagnetic theory development, concepts remained in a state of flux. Terms like “potential,” “potential difference,” “voltage,” “electromotive force,” and “electric tension” were used by investigators in contradictory and inconsistent fashions [[xvii]]. More on those ambiguities later. For now, consider the two fundamentally different models we see emerging.
On the one hand, we have valid formulas from Coulomb, Ampère, Green, and others that suggest electromagnetic action propagates instantaneously from one place to another without any specific process or intermediate steps. This is the action-at-a-distance model inspired by Isaac Newton (1642–1727) and brought to fruition by Roger Boscovich (1711–1787). On the other hand, we have Faraday’s fields which suggest electromagnetic action propagates gradually through processes distributed throughout the surrounding space. This field model is a successor to the Aristotelian plenum and the Cartesian vortices in the æther. We also have the first hints that there may be a mathematical model for describing them, thanks to William Thomson.
The situation is not as clear-cut as this broad distinction between action-at-a-distance and field models might make it appear. For instance, we will see attempts to account for a finite speed of propagation within the action-at-a-distance model, and we will see attempts – like those of Faraday – to explain fields in terms of an æther comprising Boscovich’s point-particles interacting with their adjacent neighbors.
One may demonstrate the mathematical equivalence of action at a distance and fields using some of the basic principles of potential theory identified by George Green (specifically, Green’s First Identity) [[xviii]]. Both approaches are mathematically correct and correspond to the results of measurement. The two approaches are both correct, but offer profoundly different implications for how electromagnetism works.
How these two fundamentally different approaches to electromagnetism were mathematically reconciled is a story for the next section. However, we can develop an intuition for how Faraday’s fields behave that will serve us in our understanding of electromagnetic phenomena just as they served Faraday.
What are some of the basic principles of field theory?
(1) Electric field lines show the direction of the force that would act on a small “test charge.” A test charge is a hypothetical point charge with such a small magnitude that it does not appreciably perturb the surrounding fields or nearby charge distribution.
(2) Magnetic field lines show the direction of the torque that would align a small compass needle. By convention, a “north pole” is a locus from which field lines diverge, while a “south pole” is a locus towards which field lines converge.
(3) The field line density is proportional to the field intensity and the magnitude of the corresponding force. In other words, a denser concentration of field lines indicates a stronger field. The magnitude of the force experienced by a charge or the torque experienced by a magnetic dipole is also proportional to this intensity.
(4) Field lines distribute themselves to maximize space between lines. The field lines spread out as one moves away from a source, corresponding to the decreased intensity with distance.
(5) Electric field lines begin on positive charge and end on negative charge, or form closed loops. By convention, they point out from positive charge and into negative charge. In an isolated free-space electromagnetic wave, the electric field lines form closed loops. There are no positive and negative electric charges traveling with the wave.
(6) Electric field lines are perpendicular to conductors at equilibrium. If there were a field component parallel to the surface of a conductor, it would cause the charges to move and rearrange themselves until equilibrium was restored.
(7) Magnetic field lines always form closed loops. They don't have starting or ending points. This indicates that there are no magnetic monopoles. Isolated north or south poles have not been observed. A north magnetic pole is always paired with a south magnetic pole.

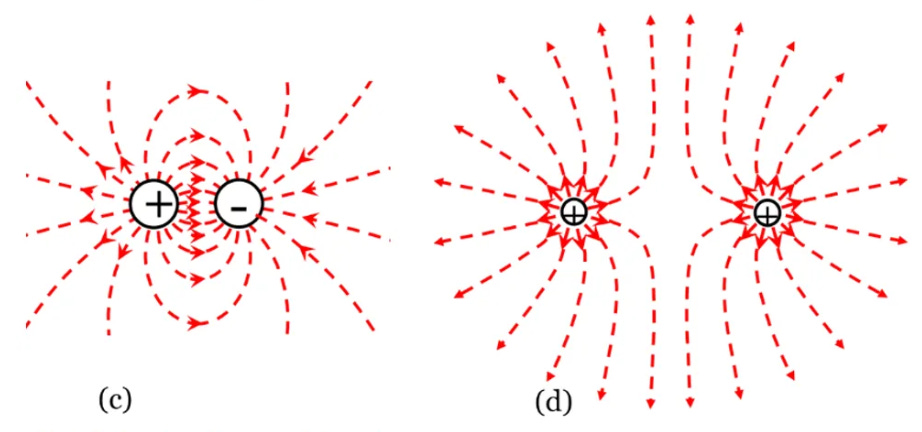
Figure 3.11 shows some simple cases of electric field lines. Positive charges are the source of electric field lines; the field lines radiate away from positive charge as in (a). Negative charges are the sink for electric field lines; the field lines converge toward negative charge, as in (b). These diagrams are a bit misleading or at least incomplete, because they show field lines spreading out into space with no termination, as in (a), or no source, as in (b).
The actual situation is more like (c), a diagram of the field lines around equal and opposite charges. Although we cannot know for certain if this is universally true, at least locally there always exists a balance of charge – equal amounts of positive and negative charge. In a complete, comprehensive, and accurate diagram, every field line begins on a positive charge and terminates on a negative charge. In the diagram of (c), for every field line leaving the diagram, there is another field line entering. The diagram crops the distant field-line geometry.
The field line pattern around two like charges looks something like (d). We have to imagine that somewhere outside the diagram bounds we have some unseen negative charges to serve as a sink for the field lines radiating out from the two positive charges.
A more practical field distribution appears in (e), showing the field lines for a conducting sphere in an applied electric field. Although the conductor is electrically neutral, the applied field induces a charge separation that exactly cancels out the field inside the sphere. Positive charge concentrates on one end of the sphere and an equal and opposite amount of negative charge concentrates on the opposite end of the sphere. The sphere becomes a “Faraday Cage:” a closed conducting shell which excludes any external field. In 1836, Faraday created a 12-foot wire-covered cube in the lecture hall at the Royal Institute in London [[xix]]. He used it to demonstrate that charge redistributes itself on the conducting walls in such a way as to cancel out the fields within.
Finally, we see a cross-section of a parallel plate capacitor in (f). This device concentrates electric fields and stores energy between parallel conducting plates. We may imagine a small positive charge at the source of each field line and a small negative charge at each arrowhead termination on the conductor. The field lines concentrate between the plates and spread out beyond and outside the plates. Charges concentrate at the edges of the plates as the charges on each individual plate repel each other to get as far apart as possible while being attracted to the opposite charge on the opposing plate. The higher density of field lines means there’s a corresponding higher concentration of charge there. The field lines are always perpendicular to the conductors.

Figure 3.12 shows surface plots of the corresponding potentials along with equipotential contours for each of the field plots of Figure 3.11. Fields show the electric force per charge. Potentials show the electric energy per charge. The equipotential lines are like elevation contours on a map: the higher up you are, the greater your gravitational potential energy. Similarly, the higher your electric potential, the greater your electric potential energy. A ball will roll down a hill in the direction of greatest slope, at a right angle to the altitude contour. An electric charge will feel a force that moves it perpendicular to the equipotentials. Electric field lines are always perpendicular to equipotential lines.
In (a), we see the equipotential peak associated with a positive charge. In (b), we see an equipotential hole associated with negative charge.
In (c), we combine opposite charges and observe the pattern of equipotentials as a positive peak yields to a negative hole. In each case, the plots are truncated, because the peaks or troughs would get infinitely high in the limit as we approached the positive or negative charge. In (d), we see the twin potential peaks of two positive charges in close proximity to each other.
The uniform field of (e) is a sloped plane in potential space. The surface of the sphere is a level equipotential. The figure might suggest that the inside of the sphere is at the same potential as the outside, but the inside potential is undefined. The inside of the sphere is electrically isolated from whatever might be happening outside.
Finally, the potential surface for the parallel plate capacitor of (f) looks like the equal and opposite charges of (c), only stretched and distorted since the entire plate is an equipotential. The white lines in (f) extending parallel to the plates are a mathematical artifact called a “branch cut” where the potential is undefined because the potential formula requires taking the logarithm of a negative number.
Potentials and fields are both correct – and complementary – ways of looking at and understanding how electricity and magnetism work. This discussion emphasized electric fields and potentials, but similar depictions are possible for magnetic fields and potentials.
Faraday’s ingenious field approach to electromagnetism lacked a thorough analytical exposition, however. New mathematical discoveries were necessary to cope with the problems Faraday’s fields posed. The genius most responsible for coloring in Faraday’s lines of force with a rigorous mathematical treatment was a physicist from Scotland, whose name would become synonymous with electromagnetism: James Clerk Maxwell.
Next time, 3.4 James Clerk Maxwell.
Follow Online:
You may follow me online in other places as well:
Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞
Gab: @aetherczar
Twitter: @aetherczar
Amazon: Hans G. Schantz
References
[[i]] As quoted by Ivan Tolstoy, James Clerk Maxwell: A Biography, (Chicago: The University of Chicago Press, 1981, p. 69.
[[ii]] Lagrange, J L, Oeuvres 6 (Paris: Gauthier-Villars) 1873, pp 349-50, 355, 775-8.
[[iii]] Laplace, P-S, Mécanique celeste, Engl. transl. N Bowditch 4 vols, (Boston,MA: Hillard, Gray, Little and Wilkins) 1 1829 – 1834 p. 280.
[[iv]] Poisson, S D, Mémoire sur la distribution de l’électricité à la surface des corps conducteurs, Mémoires de la classe des sciences mathématiques et physiques de I’lnstitut de France Année 1811 1811, 14, 30
[[v]] Cannell, D.M., “George Green: An Enigmatic Mathematician,” The American Mathematical Monthly, vol. 106, no. 2, February, 1999, pp. 136-155. doi:10.2307/2589050
[[vi]] By François Séraphin Delpech - http://www.sil.si.edu/digitalcollections/hst/scientific-identity/CF/display_results.cfm?alpha_sort=P http://www.sil.si.edu/digitalcollections/hst/scientific-identity/fullsize/SIL14-P005-06a.jpg , Public Domain, https://commons.wikimedia.org/w/index.php?curid=378439
[[vii]] By Morgan & Kidd - [1], CC BY 4.0, https://commons.wikimedia.org/w/index.php?curid=33243878
[[viii]] Green, George, 1828 An Essay on the Application of Mathematical Analysis to the Theory of Electricity and Magnetism (Nottingham: Privately published) pp vii, 1-2.
[[ix]] https://commons.wikimedia.org/wiki/File:Green%27s_windmill.jpg
[[x]] Gray, Andrew, Lord Kelvin: An Account of his Scientific Life and Work, New York: E.P. Dutton, 1908, p. 74.
[[xi]] Thompson, Silvanus Phillips, Life of William Thomson, Baron Kelvin of Large, Volume 1, London: Macmillan and Co., 1910, pp. 84, 108- 119, 141. See: https://archive.org/details/b31360403_0001/page/140/mode/2up?view=theater
[[xii]] Portrait of H. L. F. von Helmholtz, by Jeans. Credit: Wellcome Collection. CC BY
[[xiii]] Whittaker, Op. Cit., p. 218.
[[xiv]] von Helmholtz, Herman, “On the Conservation of Force,” collected in Scientific Memoirs selected from the Transactions of Foreign Academies of Science and from Foreign Journals – Natural Philosophy; John Tyndall and William Francis, editors. London: Taylor & Francis, Printers and Publishers to the University of London, 1853, p. 138-139. See: https://books.google.com/books?id=C1i4AAAAIAAJ&newbks=1&newbks_redir=0&dq=helmholtz%20on%20the%20conservation%20of%20force%201847&pg=PA138#v=onepage&q=electric&f=false .
[[xv]] Whittaker, Op. Cit. pp. 221-224.
[[xvi]] Thomson, William, “On the Mechanical Values of Distributions of Electricity, Magnetism, and Galvanism,” Proceedings of the Philosophical Society of Glasgow, Vol. III 1848-1855, Glasgow: Richard Griffin & Company, 1855, pp. 231-235. Paper originally read January 19, 1853. See: https://books.google.com/books?id=z-0UAAAAIAAJ&newbks=1&newbks_redir=0&dq=proceedings%20glasgow%20philosophical%20society%201853&pg=PA281#v=onepage&q=thompson&f=false
[[xvii]] Roche, John, “A perfect semantic storm? Attempting to resolve the ambiguities in the terms ‘potential’ and ‘voltage,’” January 21, 2019. See: https://www.academia.edu/38762138/A_perfect_semantic_storm_Attempting_to_resolve_the_ambiguities_in_the_terms_potential_and_voltage
[[xviii]] Schantz, Hans G., The Art and Science of Ultrawideband Antennas, 2nd ed., Boston: Artech House, 2015, pp. 279-281. See: https://amzn.to/4a4C4D9.
[[xix]] Faraday, Michael, Experimental Researches in Electricity, vol. 1, London: Bernard Quaritch, 1839, §1173, p. 365








I had never heard of George Green. Nevermind his Identities or Functions.
The fact that he worked out the discoveries that Chasles, Strum, Liouville, and Gauss all viewed as their own original work, implies a formidable intellect of his own .
Perhaps on a level with Tesla?
So it was William Thomson, later known as Baron Kelvin, who introduced the concept of free energy?