Yes, this is a long post, and it may have been truncated by your email client. Click on the title to be transported to the complete web-hosted version.
The most recent Fields & Energy post on Ampère’s Law represents a milestone in my development of how electricity and magnetism work. Up until this point, I’ve been presenting the historical foundations of physics in general and electromagnetism in particular as developed by other people: Newton, Coulomb, Ampère, Faraday, Ohm, Gauss, Maxwell, and all the rest. In the last post, however, I introduced a very fundamental concept that is original to me: the right-hand rule for radiation. At least, I think it’s my discovery. Unless John A. Wheeler knew it all along. I can’t be certain.
Don’t worry, history fans. There’s much more of the historical fundamentals to cover. I thought it would be interesting, however, to digress a moment and explain where I started from, and how my first (possibly) original electromagnetic discovery was the key that unlocked my doctoral research and made it all obvious (at least to me).
Further this is another great example of how something very simple and yet very profound was overlooked by generations of physicists.
I’ll begin at the beginning and set the stage. The year is 1993, and I’m a graduate student at the University of Texas at Austin. At one point in my doctoral program in theoretical physics, I resolved to figure out how gravitational energy works. My advisor, Professor E.C. George Sudarshan (1931-2018) was skeptical. “No one understands how energy works in electromagnetism,” he explained. “Why don’t you start there?”
I did not appreciate how good his advice was, at first. After all, every student of electromagnetism knows exactly how radiation works, right? Maxwell figured it all out, we have his equations, and there’s nothing left to discover, right?
I was wrong and Sudarshan was right.
I’ve managed to make an entire career out of uncovering hidden truths and neglected physics to learn how electromagnetism works. In doing so, I figured out a host of simple but overlooked principles that, taken together, led me to my model of fields guiding energy.
Let’s begin with the conventional but erroneous wisdom: that the kinked-field-line model of radiation explains how it works.
When I was in grad school, I was working from the second (1985) edition of Purcell’s excellent Electricity and Magnetism. The third edition has an identical figure explaining very clearly how radiation is just a transverse kink in a field line. Here’s the concept:
Field lines radiate outward from a charge.
We change the motion of the charge, somehow.
The change involves a field line with a transverse component (Eθ in the figure, below) connecting the field lines as they were to the field lines as they are, now.
The shell caused by that change ripples outward at the speed of light.
Voilà, radiation.
Purcell’s figure illustrates this.
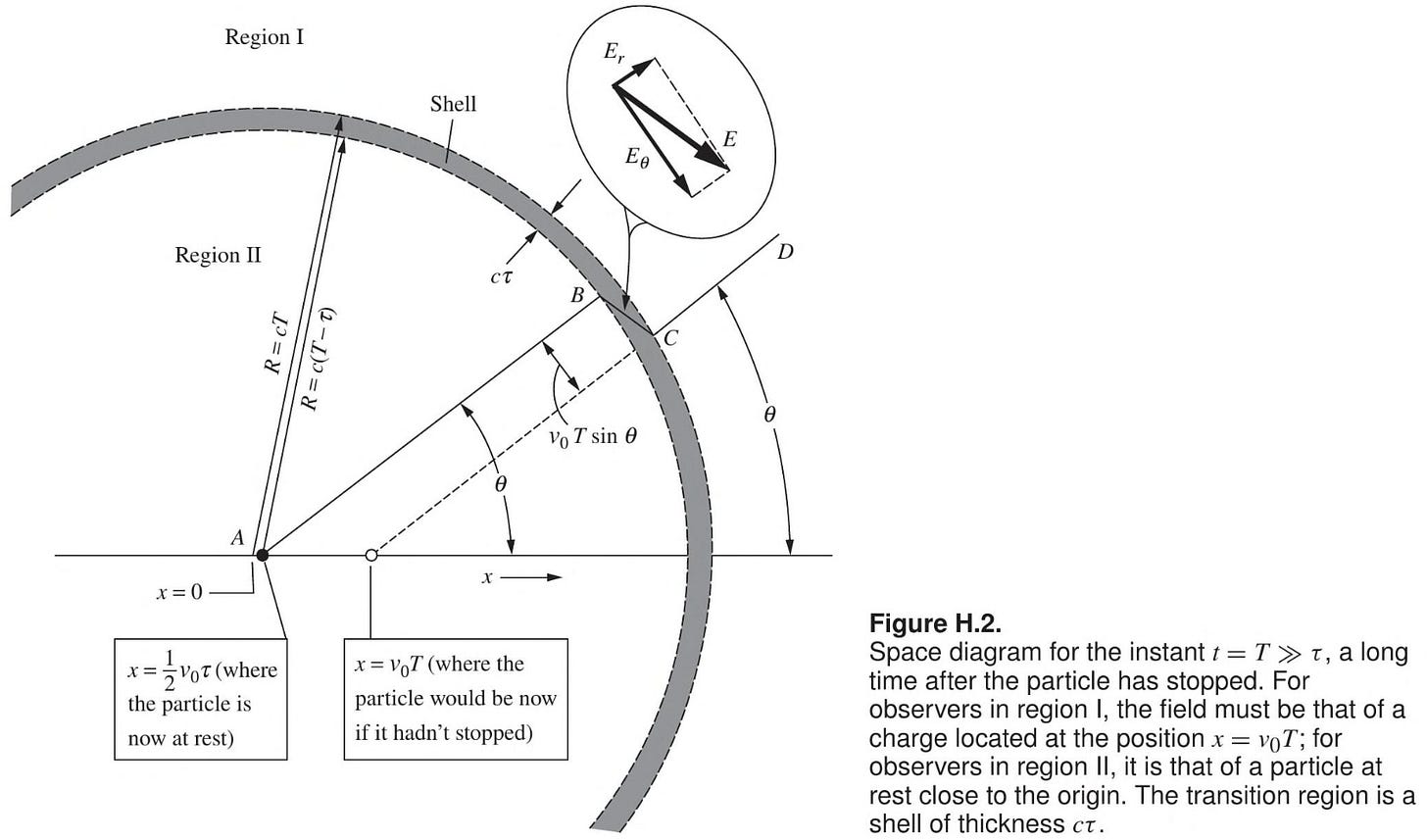
The concept is so fundamental that it’s on the cover of the book.

This “radiation-is-a-kinked-field-line” thinking is almost ancient history as far as physics is concerned. The earliest very clear depiction of this kind I’ve found is from Electricity and Matter in 1904, written by the discoverer of the electron, himself, J. J. Thomson (1856-1940).
Imagine a charge originally at a point O' with a field line O' P' Q'. Suddenly the charge is snapped to point O. What would have been the O' P' Q' field line adapts to the change, becoming field line O P Q. The transition is not instantaneous, however, because electromagnetic fields propagate at the speed of light. Thus, if we examine the field line not long after the charge halts, we will observe a transverse component P P' propagating out. This transverse field line P P' is the locus where the O' P' Q' field line becomes the O P Q field line.
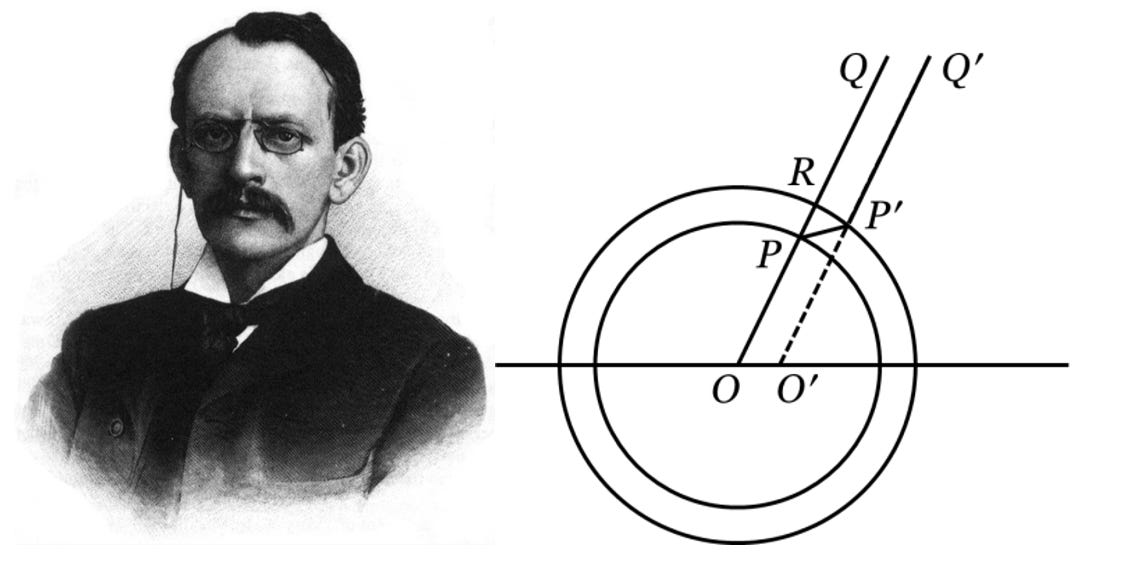
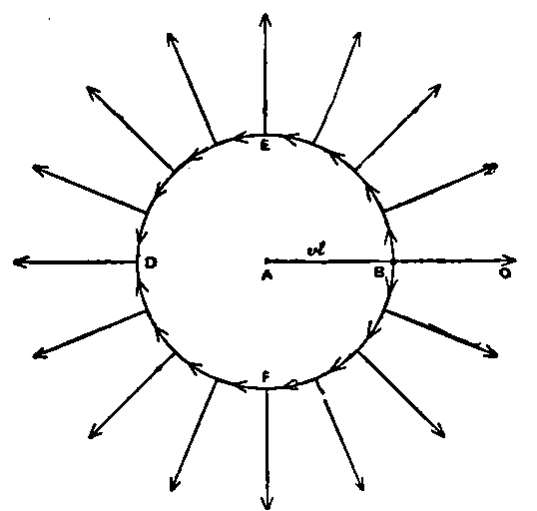
Arguably, Oliver Heaviside (1850-1925) pioneered this kinked-field-line thinking. In 1893, he imagined a charge originally at a point A suddenly accelerated to the speed of light in a direction AC [[i]]. Heaviside argued that the field lines would be analogous to lines of longitude on the sphere described by B, D, E, and F, centered at A and with an axis traversing B and D.
In 1912, George Adolphus Schott (1868-1937) wrote his Adams Prize Essay, “Electromagnetic radiation and the mechanical reactions arising from it,” with quite elaborate diagrams of kinked field lines.
Schott is notable for his proof that there exist oscillatory periodic motions of charge distributions that do not emit radiation, but that is a topic for a different post.
I soon realized that the kinked-field-line model is deeply flawed, however.
Radiation isn’t kinky!
Put simply, an isolated charge never radiates by itself. It must be acted upon by another charge. All those field lines radiating off to infinity? They have to terminate in an equal and opposite charge distribution. In free space, in the absence of a charge or current distribution, Gauss’ Law demands that electric field lines form closed loops. If the field lines don’t form closed loops, you are looking at field details within a source distribution, not radiation.
The kinked-field-line model focuses on the trees of individual point charges to the exclusion of the forest of the larger electromagnetic system within which those point charges operate. In so doing it delivers a partial, distorted, and misleading picture of what’s happening. It conflates the part with the whole. This is the fallacy of composition: an informal fallacy that arises when you infer that something is true of the whole because it is true of some part of the whole.

The flaws of the kinked-field-line model are just the beginning.
Oliver Heaviside (1850-1925) and John Henry Poynting (1852-1914) worked out the basics of how electromagnetic energy moves from place to place in 1884-1885, but the details can be tricky. Except for some of the most simple cases, like far-field links between antennas, their theory remains more a curiosity than an everyday practical engineering tool. Those confusions and their resolutions are a topic for future posts.
The challenge Sudarshan posed was for me to show how electrostatic energy becomes radiation energy. The easiest way to do that is to start with a dipole: equal and opposite electric charge. Imagine a capacitor of capacitance (C) with equal and opposite charge (±Q) that we discharge through a resistance (R). The capacitor may be thought of as a dipole with equal and opposite charge (±Q) or equivalently, once it begins discharging, as a short current (I) with length L. The discharge current of the capacitor depends on how much charge there is to set up a voltage difference to drive the current. Initially, the large amount of charge pushes a large amount of current through the resistor. As the capacitor discharges, less and less charge remains. The current decreases further and further, so the change in current is in the opposite direction of the current. Mathematically this is an exponential decay, and further mathematical details I’ll leave to the caption below.
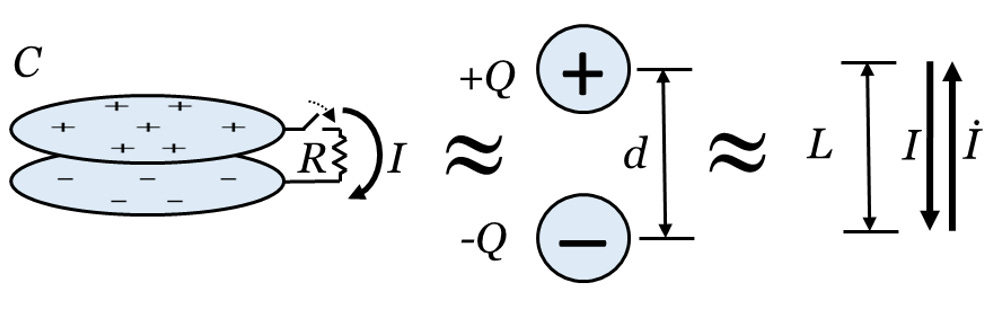
This is a beautifully simple yet profound example. We start with purely electrostatic energy. We end with radiation. We can example the process step-by-step to see exactly how the bound, static energy decouples and becomes radiation.
I found something remarkable. There is a bubble around the exponential decay whose radius (r) is the speed of light (c) times the time constant (τ): r = c τ = c RC. Here’s an animation of the electric field lines. The horizontal and vertical distance units are scaled in units of c τ and the time (at top center) is in units of τ.
Inside the bubble, energy is absorbed and converted to heat in the resistor. Only outside the bubble does energy start flowing away. I dubbed this bubble a “causal surface,” since it separates the two causally distinct energy zones.
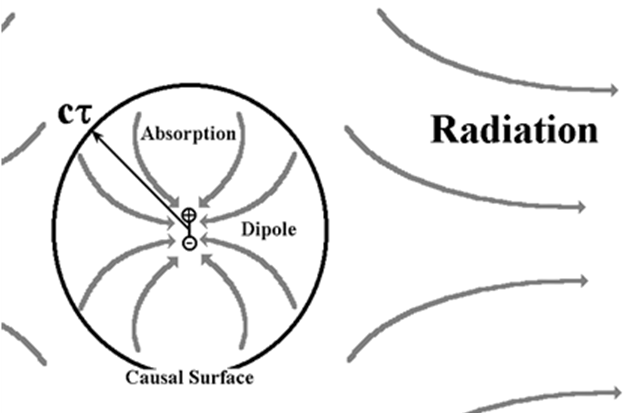
In fact, a more detailed calculation shows that the radiated energy in the tail of the exponential decay is exactly equal to amount of electrostatic energy stored outside the bubble. The radiation fields ripple out through an in-falling flux of energy. Only past the bubble do the radiation fields couple to and guide outward flowing energy. And the energy they convey is the energy that was originally stored outside the bubble.
These results cannot easily be reconciled with the conventional perspective that radiation is a cloud of photons streaming away from accelerating charges. In the wake of the wave front’s passage within the bubble, energy is moving in. Outside the bubble, the energy begins moving out, and the total amount of radiation energy is exactly the same as the amount of static field energy stored outside the bubble. The conclusion that the radiation energy did not come from the accelerating charges but instead was picked up by the radiation fields outside the bubble appears inescapable.
The final challenge I had was how to understand and explain what was going on when I was grilled by my dissertation committee. I had help from one of the other members of my committee, John A. Wheeler (1911-2008).
Wheeler was an emeritus professor at UT Austin by that point. He still lived in Princeton, but he came to Austin a few times a year, and he was very generous with his time. We talked about my research in particular, physics in general, and history. He had a wonderful Socratic style of leading me on. And that’s why I’m not entirely sure whether the right-hand-rule for radiation was my idea or whether it was really Wheeler’s idea and he just nudged me toward it. It’s such a clever and useful concept, I’d think if it were Wheeler’s idea, famous as he was, more people would have heard of it. Or maybe it truly was a collaborative effort.
The right-hand rule for radiation pops out immediately when you look at an expression for the magnetic field pioneered by Oleg Jefimenko (1922-2009). What’s more, you don’t have to understand vector calculus or the retarded evaluation implied by the square brackets to see what’s going on. The left term in his Biot-Savart Law? That’s the induction magnetic fields around an elemental bit of current density (J). It’s the mathematical form of the right-hand rule. What’s with the term on right side? It has a nearly identical form except it depends on the rate of change of the current and it goes as inverse distance (1/x) instead of the inverse distance square (1/x2) dependence of the induction term. That means the magnetic radiation field also follows a similar right-hand rule that depends on the rate of change of the current.
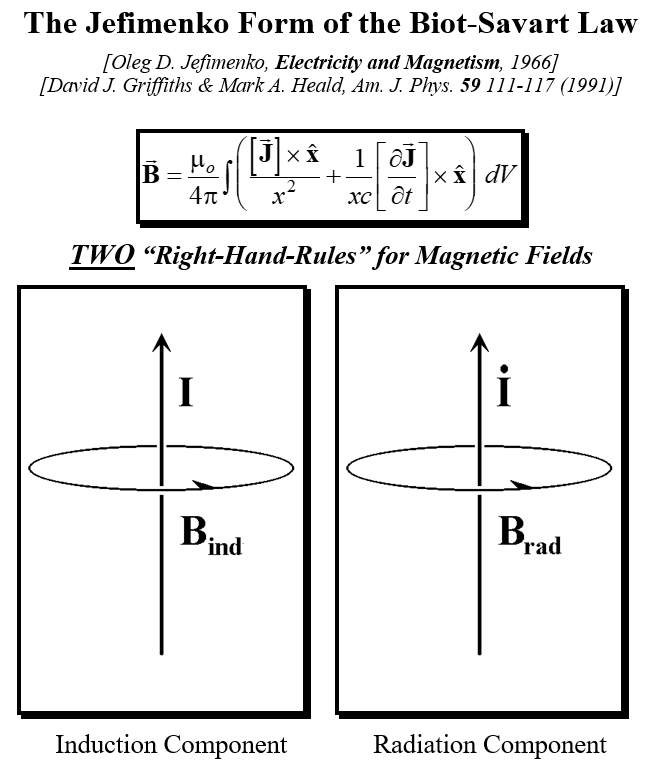
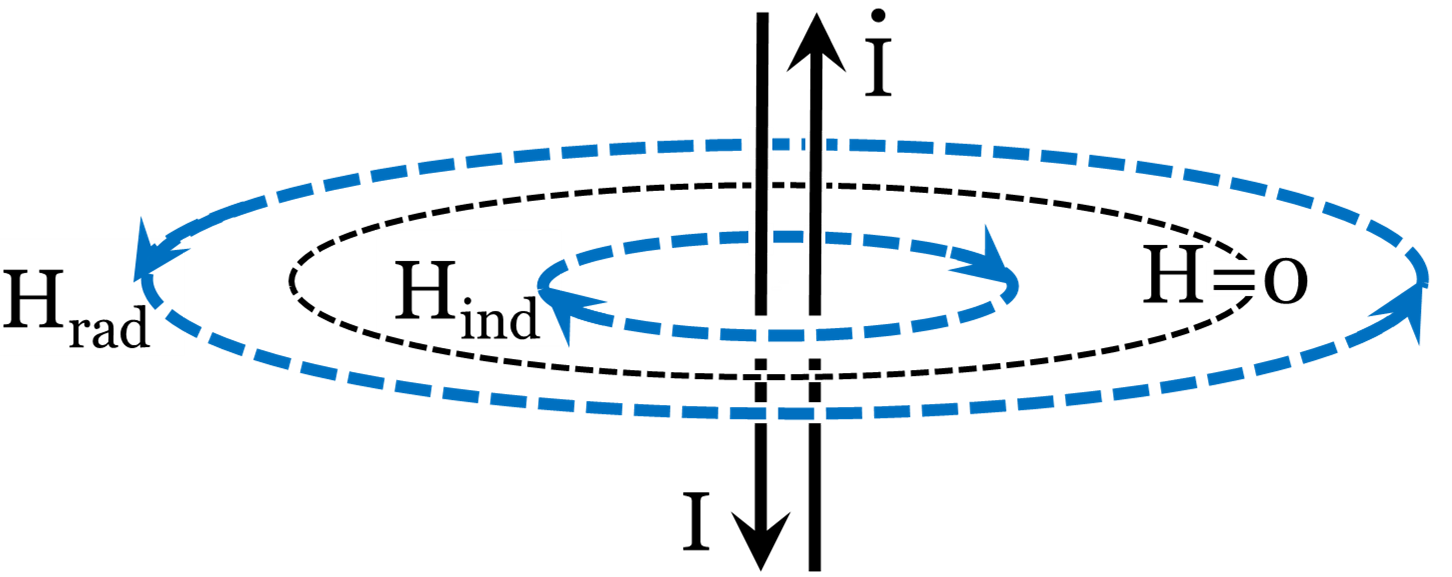
The right-hand rule for radiation makes it easy to understand what’s happening. Suppose the current is down for a particular discharge, and the induction magnetic field - which dominates close to the source - is clockwise. The change in current points in the opposite direction, so the radiation magnetic field is counter-clockwise. The radiation magnetic field dominates further away. The two components of the magnetic field are in different directions, so at some intermediate distance, the magnetic field has to be zero. Calculate the magic distance (r) where the magnetic field goes to zero, and you get r = c τ. Since the magnetic field goes to zero (H = 0), the Poynting vector (S = E x H = 0). The diagram below uses “H” for magnetic field instead of “B” for magnetic flux, but the distinction doesn’t matter for our purposes, here.
Further details of the exponential dipole decay including the exact expressions for the fields and their impedance are equations 3.1-3.3 in my 2018 paper on “Energy velocity and reactive fields.”
The kinked-field-line model isn’t particularly useful for solving practical problems. The right-hand rule for radiation, on the other hand, can be applied to obtain an intuitive understanding of some complicated problems. Here’s a problem Wheeler had me work through with him in private discussion. He then asked me to solve this in the oral questioning period of my final defense.
Problem: Suppose a solenoid is radially compressed inward in a sudden compression at a particular point along its length. Describe the radiation pattern.
Solution: At the point of compression, the change in current is radially inward in a disk. Above the disk of radially compressing current, the radiation magnetic field rotates one way. Below the disk, it rotates the other way.
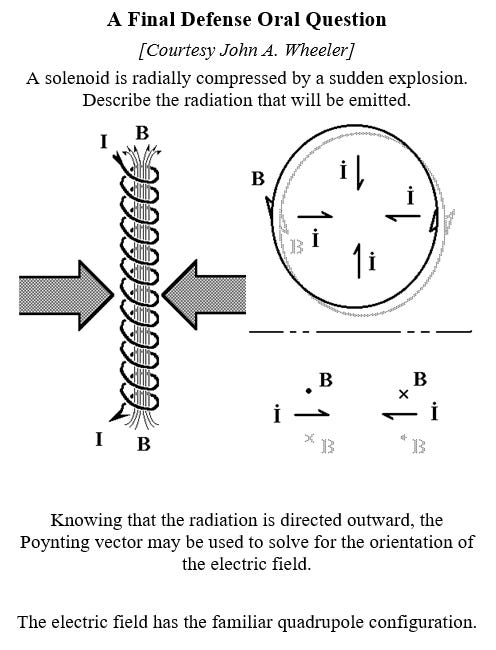
The resulting radiation pattern is below. I used this as a worked example in my UWB antenna textbook (2nd ed.).
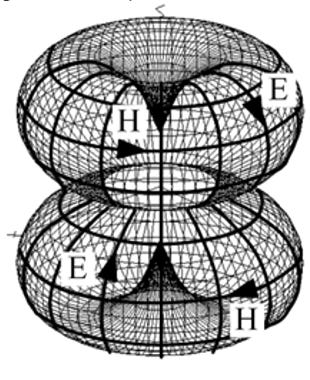
This entire post is a preview of material from Chapter 8 of Fields & Energy, but I thought it would be interesting to explain the right-hand-rule for radiation in more detail, now that I’ve introduced it.
The example of this post is one of many simple electromagnetic problems that defies explanation using the currently understood model. Contemporary physicists are quick to jump to solving problems under the assumption of the point-charges-emitting-point-photons model. When challenged, they then fall back to “shut-up and calculate,” and deny they are using a model or interpretation whatsoever. They admonish researchers and students alike to do the math, and ignore models and interpretations. No physical interpretation or simple picture is possible, they claim.
And yet, the example of the exponentially decaying dipole becomes easy to understand when you realize that fields and energy are two complementary yet distinct and different phenomena, with different behavior and different trajectories. They cooperate to give rise to electromagnetism, but they may be looked at individually and on their own terms as separate phenomena.
Back to the mainstream of the Fields & Energy narrative Wednesday May 1 with 3.4.5 Faraday’s Law & Electromagnetic Waves: Maxwell’s Theory Suggests Light is an Electromagnetic Wave.
Follow Online:
You may follow me online in other places as well:
Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞
Gab: @aetherczar
Twitter: @aetherczar
Amazon: Hans G. Schantz







Sure! Run it past me though, if you don't mind, so I can make sure it makes sense.
Excellent post! Yes, the two right-hand rules makes so much sense, and highlights why the phrase "the important stuff tends to happen at the boundaries". Your animation is worth half-a-dozen hour lectures on the topic.
This is why my notebooks from graduate school were filled with drawings, diagrams, and speculative pictures. To deny that images and doodles cannot help you, even in the esoteric world of QM, speaks to attempts to deny the benefits of imagination to the fields of Science.