4.4.2 The Catt Question
How Does a Net Charge Get On A Wire?
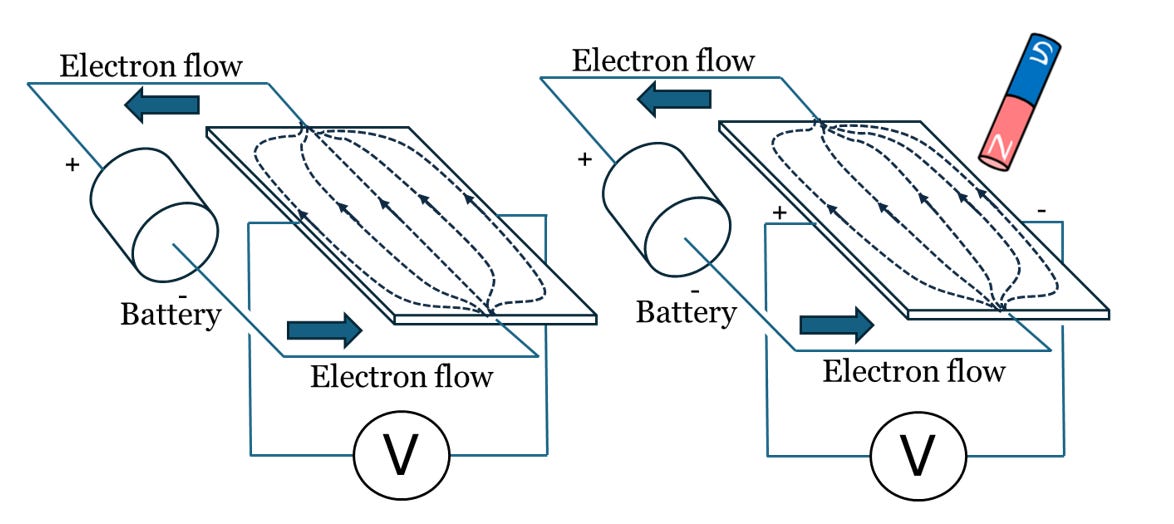
Ivor Catt (1935– ) posed the question “When a voltage step travels down a transmission line at the speed of light guided by two conductors, where does the negative charge come from on the bottom conductor to terminate the electric field between the conductors?” [[i]]
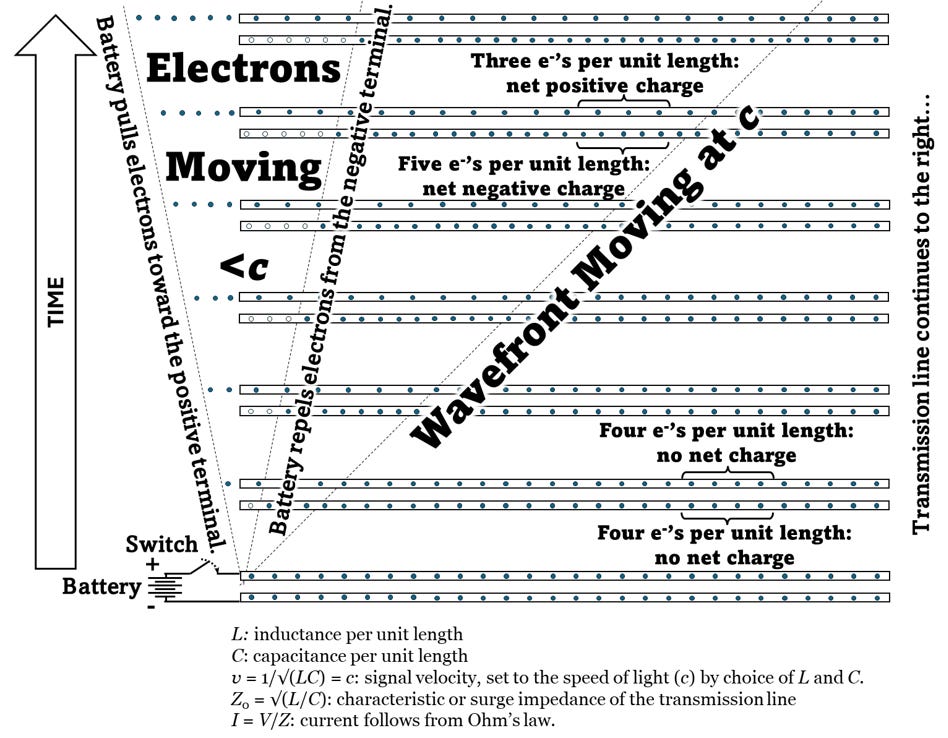
Typical transmission lines have a signal velocity less than the speed of light, but we will assume ours, shown in Figure 4.43, is in a vacuum and designed so fields propagate at the speed of light. The transmission line is initially electrically neutral with four free electrons per unit length (shown as dots) balanced out by an equal and opposite amount of positive charge (not depicted) which remains unmoved. A battery at one end applies the voltage step and sets fields in motion down the line at the speed of light. In the wake of the step (not sinusoidal!) wavefront, the transmission line has a net positive charge on the top wire (with three electrons per unit length) and a net negative charge on the bottom wire (with five electrons per unit length. The positive battery terminal pulls electrons out of the top conductor while the negative terminal pushes them into the bottom conductor.
This deceptively simple-looking problem has caused much controversy. Some claim it refutes the concept of charge because it implies charge must move at the speed of light to keep up with the wavefront [[ii], [iii]]. To the contrary, a charge density step wave follows the field step wavefront at the speed of light. Slight increases or decreases in electron density yield a net negative or net positive charge. Electrons themselves move much more slowly.
This example does offer an interesting illustration of the fluid-only model’s shortcomings. Charges are not billiard balls that must lurch forward at the speed of light to bump into the next charges along the line. They do not act alone. Instead, as demonstrated by the phenomenon of skin depth, the fields propagating outside the wire set the charges in motion within the wire, starting at the surface and permeating inward. A fluid model comprising only charges acting mechanically with contact forces cannot account for the behavior of a voltage step applied to the transmission line. However, the charge carriers or electrons are a critical part of electromagnetic phenomena. How do we know this?
In 1879, a young graduate student at Johns Hopkins University, Edwin Herbert Hall (1855-1938), reasoned that if magnetic fields specifically act upon current, then an applied field acting upon a current-carrying wire should cause a slight voltage difference as charge crowds on one side of the wire in response to the applied magnetic force. He successfully measured what came to be known as the Hall Effect for his doctoral research [[iv]].
In 1916, Thomas Dale Stewart (1890–1958) and Richard Chase Tolman (1881–1948) provided a comprehensive study of the electromotive force or voltage associated with the acceleration of metals.
The modern theories of electricity have led to the belief that the passage of an electric current through a metal really consists in the progressive motion of “free” electrons contained in the body of the metal itself. If this be true we may now expect a number of effects arising from the mass of these electrons which were not predictable on the basis of older theories which thought of electricity as a sort of intangible massless fluid. As examples of such effects, we should expect the rear end of an accelerated rod of metal to become negatively charged owing to the lagging behind of the relatively mobile electrons which the metal contains, and should expect the periphery of a rotating disk to become negatively charged owing to the action of centrifugal force on the electrons in the disk [[viii]].
The ”Stewart-Tolman” effect [[ix]] is easier to detect in electrolytes, because their charge carriers are relatively massive ions, but Stewart and Tolman were able to provide a series of sensitive experimental results with conducting metals demonstrating that electricity is conveyed by small, lightweight charge carriers we’ve identified as electrons.
By the early years of the twentieth century the fluid theory of electricity was in its proper place as an adjunct to fields guiding energy. Paul Karl Ludwig Drude (1863–1906) modeled conduction charges as an ideal charged gas moving within a positively charged lattice, Joseph John “J.J.” Thomson (1856–1940) identified those charge carriers as the “electrons” in his cathode rays, and Hendrik Antoon Lorentz (1853–1928) combined their ideas with those of Maxwell to create his electron theory [[x]]. Although a more precise and detailed picture would soon emerge, particularly with respect to semiconductors and superconductors, quantum physics only refined the pre-existing model of electrical conduction. Quantum physicist John C. Slater (1900–1976) declared:
…it turns out to work in such a way that the results we have been stating, regarding the conductivity, effect of scattering, and so on are still substantially correct. It is this fact which made it possible for a considerable period to use the classical theories of Drude and Lorentz, without serious trouble [[xi]].
The transmission line of our example shows a one part in four decrease or increase in charge density. The electrons are moving at about a quarter of the speed of light. In a real transmission line, the changes in charge density are much, much smaller, proportionally. Consider a hefty 10-Amp current flowing in a copper battery cable. An “Amp” or “Ampère” is a unit of current equal to one Coulomb of charge per second. A Coulomb is a unit of charge equivalent to the charge of 6.242 × 1018 electrons. A cubic centimeter of copper has just under 14,000 Coulombs of conduction charges assuming one free electron per atom of copper. In a second, 10 Coulombs of charge pass out of that cubic centimeter of copper, 10 Coulombs pass in, and the balance of 13,900 Coulombs remain. It takes 23 minutes for a 10-Amp current to completely refresh the conduction electrons in a cubic centimeter of copper and move them to the next cubic centimeter down the battery cable. Even a large current by everyday standards involves the actual charges moving a few tenths of a millimeter per second [[xii]].
The examples of Figure 4.40 and 4.43 show how the more mobile electrons are compressed a bit relative to the fixed background of positive atomic ions to yield a net negative charge or stretched out a bit to yield a net positive charge. Fields and energy propagate along the wires at the speed of light. In the wake of the wave front’s passage, the slow drift of charge in the wire compressing or rarefying the charge density accounts for both the current and the net charge. Charge does not travel with the wave. Instead, the wave’s passage rearranges the charge. The answer to Catt’s question on the origin of the charge is that the charge was already there.
Charge is not a passive participant in the process. The interaction of charges with the lattice absorbs and dissipates energy giving rise to resistance. Conduction is a complex process in which charges, currents, fields, and energy are coupled to give rise to physical effects.
A wave is a progressive transference of energy, not necessarily of matter. Even when a tsunami propagates across an ocean in a matter of hours, no water moves the entire distance. Locally, the potential and kinetic energy of the water near the source of the tsunami impart energy to adjacent water imparting energy in turn.
All these examples give us a foundation to understand how electromagnetism works and what models explain its behavior. Let’s look at those models and see which ones we need and how they work together.
Next time: 4.5 An Introduction to Electromagnetic Models: How Does it Work?
Full Table of Contents [click here]
Chapter 4 Electromagnetism Comes of Age
4.5 An Introduction to Electromagnetic Models
4.5.1 Potentials and Actions at a Distance
4.5.2 Jefimenko & Lorentz
4.5.3 A Synthesis
4.6 Hertz & Radiation Fields
4.7 How Does Radiation Work?
4.8 Summary & Conclusions
Follow Online:
You may follow me online in other places as well:
Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞
Gab: @aetherczar
Twitter: @aetherczar
Amazon: Hans G. Schantz
References
[[i]] Catt, Ivor, “The Catt Question,” Electronics World, May 2009, p. 16. See: http://www.ivorcatt.co.uk/91.htm
[[ii]] Bishop, Forrest, “The Forbidden Equation,” Proceedings of the CNPS, vol. 10, pp. 1-14. See: http://www.naturalphilosophy.org/pdf/abstracts/abstracts_paperlink_7395.pdf
[[iii]] Bishop, Forrest, “Reforming Electromagnetic Units, Equations, and Concepts: An Extension of Ivor Catt’s Theory,” Proceedings of the NPA, vol. 9, 2012, pp. 38-49. See: http://www.naturalphilosophy.org//pdf//abstracts/abstracts_6554.pdf
[[iv]] Hall, Edwin, “On a New Action of the Magnet on Electric Currents,” American Journal of Mathematics, vol. 2, 1879, pp. 287–292.
[[v]] Photo of Ivor Catt, courtesy Forrest Bishop.
[[vi]] Photo of Edwin Herbert Hall. See: https://en.wikipedia.org/wiki/Edwin_Hall#/media/File:Edwin_Herbert_Hall_(1855-1938).jpg
.jpg){kind=link}
[[vii]] Cropped from Richard C. Tolman and Albert Einstein standing in front of blackboard at California Institute of Technology in 1932. Handwriting on negative states “Dr. Richard Tolman & Dr. Einstein.” See: https://infogalactic.com/info/File:Tolman_%26_Einstein.jpg
[[viii]] Tolman, R.C., and Stewart, T.D., “The electromotive force produced by the acceleration of metals,” Physical Review, Second Series, Vol. VIII, No. 2, August 1916, pp. 97–116.
[[ix]] Landau, L.D. E.M. Lifshitz, L.P. Pitaevskii, Electrodynamics of Continuous Media. Course of Theoretical Physics, Vol. 8., 2nd ed., translators: J.B. Sykes, J.S. Bell and M.J. Kearsly, 1984. Landau et al are credited with calling this the “Stewart-Tolman effect,” although others had successfully predicted and measured the effect in electrolytes, earlier.
[[x]] Whittaker, Edmund, A History of the Theories of Æther and Electricity, vol. 1, New Tork: Harper and Brothers, 1960, pp. 418-428. Originally published 1910.
[[xi]] Slater, John, Quantum Theory of Matter, New York: McGraw-Hill, 1951, see Chapter 12: Electrical Conductivity. The quote comes from p. 350.
[[xii]] Schantz, Hans G., The Art and Science of Ultrawideband Antennas, 2nd ed., Boston: Artech House, 2015, pp. 285-286. This example is worked out in detail.
[[xiii]] Hokusai, Katsushika, “The Great Wave off Kanagawa.” Although it is often used in tsunami literature, there is no reason to suspect that Hokusai intended it to be interpreted in that way. The waves in this work are sometimes mistakenly referred to as tsunami (津波), but they are more accurately called okinami (沖波), great off-shore waves. See: https://upload.wikimedia.org/wikipedia/commons/thumb/a/a5/Tsunami_by_hokusai_19th_century.jpg/1280px-Tsunami_by_hokusai_19th_century.jpg
The way I visualize it, working at grasping the concepts your research has developed, is that electromagnetic fields are propagating reactions in an ether due to moving charges, and energy is the wave progression? Fields are a process, not a structure? Energy is the effect? (And if you don't like it, I'm not responsible for this outlandish characterization.)