4.5.1 Potentials and Actions at a Distance
Does a Body Act Where It Is Not? Weberian Electrodynamics
Potentials: We may be running short on hands, but not theories, because we may alternatively consider potentials as primary. The previous chapter looked at scalar electric potentials as an equivalent way to understand how electrostatics works. It’s trickier to understand magnetic fields as the result of potentials, because the magnetic potential is a vector field. Furthermore, nearly all the physical effects we perceive from electricity and magnetism are due to the forces: the slope of the potential. That slope is the same if you add or subtract an arbitrary constant from the potential, making it difficult to claim any particular value is the “true” potential. This so-called “gauge invariance” is a fundamental concept in modern field theory.
Action at a Distance: It is entirely possible to describe electromagnetism in terms of forces acting on charges at a distance in analogy to Newtonian central forces. This was the original method of Coulomb and Ampère. However, to capture the behavior of magnetism, forces then become functions not only of distance, but also of velocity and acceleration. Further, the forces are no longer “central,” pointing to and from the charges in question, but instead may point in other directions. This approach has a long history dating back at least to 1857 when Gustav Robert Kirchhoff (1824–1887) expounded “On the Motion of Electricity in Wires” [[i]], and when Wilhelm Eduard Weber (1804–1891), who we met previously as a collaborator with famed geophysicist Johann Carl Friedrich Gauss (1777–1855), proposed his electrodynamics in 1864 [[ii]]. These works and explanatory notes are compiled in an excellent volume edited by André Koch Torres Assis (1962– ) [[iii]]. Weber’s model deserves further discussion.
In Weber’s model, force (F) between two charges (Q and q) depends upon free space permittivity (εo) and is a function of the charges’ relative distances (r), relative velocity (v), and relative acceleration (a), normalized by the speed of light (c). Emerging evidence that the transmission of electromagnetic effects is causal, progressive, and propagates at the speed of light eroded confidence in action-at-a-distance models, like Weber’s. Even today, work is underway to revive and apply Weberian thinking.
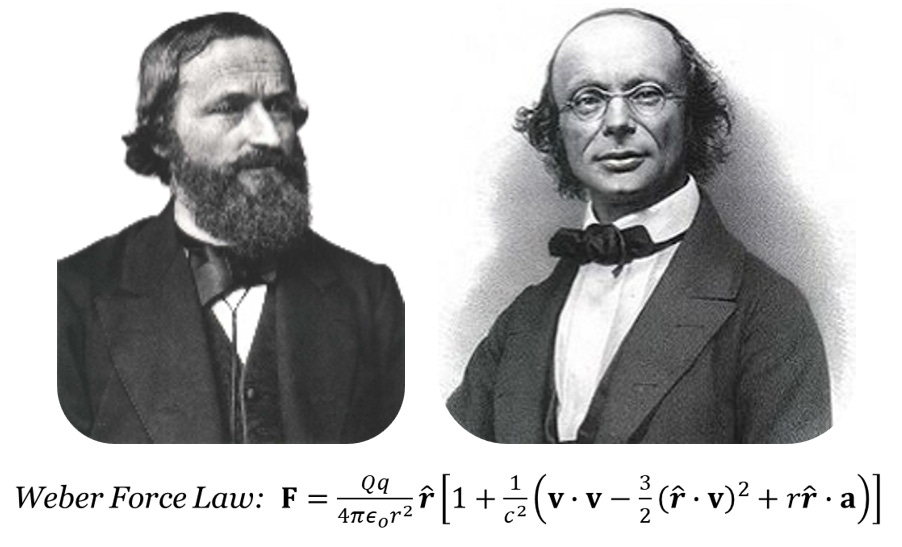
One can derive a telegrapher’s equation [[vii]] and wave equations from Weber’s electrodynamics [[viii], [ix]]. Steffen Kühn and others seek a synthesis between Weber and Maxwell [[x]].
There is no reason I know of why expressing electromagnetic interactions as direct forces between particles could not be mathematically equivalent to the Maxwellian field approach, provided the actions are retarded to account for the speed of light. The action-at-a-distance model, by focusing on interactions on charged particles enforces Newtonian action and reaction and may help expose weaknesses or flaws in the Maxwellian paradigm.
My personal objection to the action-at-a-distance model is that while it may be mathematically equivalent and useful in certain contexts, it prevents an understanding of the causal mechanism by which one charge influences another. Like Newton’s Universal Theory of Gravitation, Weber’s electrodynamics and similar theories describe what happens but frame no hypothesis for why. I find this story unsatisfying. The Maxwellian field model, as extended by Poynting and Heaviside to describe the flow of energy, holds the promise of understanding, at least in part, electromagnetism by meticulously following the progressive motion of energy from a starting cause to an ending effect as fields guide the flow of energy.
Next time: 4.5.2 Jefimenko & Lorentz: A Middle Ground Between Maxwell & Weber?
Full Table of Contents [click here]
Chapter 4 Electromagnetism Comes of Age
4.5 An Introduction to Electromagnetic Models
4.5.1 Potentials and Actions at a Distance
4.5.2 Jefimenko & Lorentz
4.5.3 A Synthesis
4.6 Hertz & Radiation Fields
4.7 How Does Radiation Work?
4.8 Summary & Conclusions
Follow Online:
You may follow me online in other places as well:
Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞
Gab: @aetherczar
Twitter: @aetherczar
Amazon: Hans G. Schantz
References
[[i]] Kirchhoff, Gustav, “On the motion of electricity in wires,” Philosophical Magazine, 13, 1857, pp. 393–412. See: https://archive.org/stream/londonedinburghp13maga#page/392/mode/2up.
[[ii]] Weber, Wilhelm, “Elektrodynamische Maassbestimmungen insbesondere über elektrische Schwingungen. Abhandlungen der Königlich Sächsischen Gesellschaft der Wissenschaften zu Leipzig, mathematisch-physischen Classe,” vol. 6, 1864, pp. 571–716. Reprinted in Wilhelm Weber’s Werke, Vol. 4, H. Weber (ed.), Berlin: Springer, 1894, pp. 105-241.
[[iii]] Assis, André Koch Torres, ed., Wilhelm Weber’s Main Works on Electrodynamics Translated into English Volume III: Measurement of Weber’s Constant c, Diamagnetism, the Telegraph Equation and the Propagation of Electric Waves at Light Velocity, Montreal: Apeiron, 2021. See: https://www.ifi.unicamp.br/~assis/Weber-in-English-Vol-3.pdf and https://amzn.to/3yyVBOL for very reasonably priced hardcopies.
[[iv]] Portrait of Gustav Kirchhoff, Smithsonian libraries (SIL-SIL14-k002-03). See: https://infogalactic.com/info/File:Gustav_Robert_Kirchhoff.jpg
[[v]] See: https://upload.wikimedia.org/wikipedia/commons/5/55/Wilhelm_Eduard_Weber_II.jpg
[[vi]] Assis, A.K.T.; Tajmar, M. Rotation of a superconductor due to electromagnetic induction using Weber’s electrodynamics. Ann. Fond. Louis Broglie 2019, 44, 111–123. From Li & Maher, Op. Cit.
[[vii]] Assis, A.K.T.; Hernandes, J., “Telegraphy equation from Weber’s electrodynamics,” IEEE Trans. Circuits Syst. II Express Briefs 2005, 52, pp. 289–292.
[[viii]] Kühn, Steffen, “Inhomogeneous wave equation, Liénard-Wiechert potentials, and Hertzian dipoles in Weber electrodynamics,” Electromagnetics, vol. 42, no. 8, 2022, pp. 571-593. DOI: 10.1080/02726343.2022.2161709
[[ix]] Li, Qingsong, and Simon Maher, “Deriving an Electric Wave Equation from Weber’s Electrodynamics,” Foundations 2023, 3, pp. 323-334. DOI: 10.3390/foundations3020024.
[[x]] Kühn, Steffen, “Weber–Maxwell electrodynamics: classical electromagnetism in its most compact and pure form,” Electromagnetics, 29 July, 2024. DOI: 10.1080/02726343.2024.2375328



Action at a distance is real for massless fields like gravity and EM and perhaps all mass less fields! Experiments and theory now show that massless fields like gravity and EM propagate instantaneously in the nearfield for regions less than one wavelength from the source, and reduce to about speed c at about 1 wavelength. After that the fields reduce asymptotically toward speed c, but are never exactly speed c even at astronomical distances from the source. They only become exactly speed c at infinite distance which does not exist. So nowhere in this universe do massless fields like gravity and EM propagate at speed c! Theoretically this has been proved by setting the wave equation to a source term in both these theories, and solving for the resultant fields. Then extracting the phase vs distance from the source relation (dispersion curve), shows that it is non linear in the nearfield, with a clear minima, and becomes approximately linear in the farfield, about 1 wavelength from the source. Applying well known phase speed and group speed operators to the curve, which are proportional to the inverse of the slope of the curve, show that the fields propagate instantaneously in the nearfield, and reduce to the speed of light in the farfield, and about 1 wavelength from the source. See the following paper for details:
https://arxiv.org/abs/physics/0603240
Since Relativity assumes the speed of light is constant for all inertial frames, then it is absolutely wrong, and so is any theory based on it it, which affects all of modern physics! Once this is understood, unification is possible. When are scientists going to wake up and look at the experiments and theory that prove that the speed of light is not a constant speed as once thought, which has now been verified by many independent researchers. Often it is stated that Relativity has been verified by so many experiments, how can it be wrong. Well no experiment can prove a theory, and can only provide evidence that a theory is correct. But one experiment can absolutely disprove a theory, and the new speed of light experiments proving the speed of light is not a constant is such a proof. So what does it mean? Well a derivation of Relativity using instantaneous nearfield light yields Galilean Relativity. This can easily seen by inserting c=infinity into the Lorentz Transform, yielding the Galilean Transform, where time is the same in all inertial frames. Also Relativity is based on 2 postulates: Galilean Relativity, and that the speed of light is a constant c for all inertial frames. If the 2nd postulate is not true, all that is left is Galilean Relativity! So a moving object observed with instantaneous nearfield light will yield no Relativistic effects, whereas by changing the frequency of the light such that farfield light is used will observe Relativistic effects. But since time and space are real and independent of the frequency of light used to measure its effects, then one must conclude the effects of Relativity are just an optical illusion.
Since General Relativity is based on Special Relativity, then it has the same problem. A better theory of Gravity is Gravitoelectromagnetism which assumes gravity can be mathematically described by 4 Maxwell equations, similar to to those of electromagnetic theory. It is well known that General Relativity reduces to Gravitoelectromagnetism for weak fields, which is all that we observe. Using this theory, analysis of an oscillating mass yields a wave equation set equal to a source term. Analysis of this equation shows that the phase speed, group speed, and information speed are instantaneous in the nearfield and reduce to the speed of light in the farfield. This theory then accounts for all the observed gravitational effects including instantaneous nearfield and the speed of light farfield. The main difference is that this theory is a field theory, and not a geometrical theory like General Relativity. Because it is a field theory, Gravity can be then be quantized as the Graviton.
Lastly it should be mentioned that this research shows that the Pilot Wave interpretation of Quantum Mechanics can no longer be criticized for requiring instantaneous interaction of the pilot wave, thereby violating Relativity. It should also be noted that nearfield electromagnetic fields can be explained by quantum mechanics using the Pilot Wave interpretation of quantum mechanics and the Heisenberg uncertainty principle (HUP), where Δx and Δp are interpreted as averages, and not the uncertainty in the values as in other interpretations of quantum mechanics. So in HUP: Δx Δp = h, where Δp=mΔv, and m is an effective mass due to momentum, thus HUP becomes: Δx Δv = h/m. In the nearfield where the field is created, Δx=0, therefore Δv=infinity. In the farfield, HUP: Δx Δp = h, where p = h/λ. HUP then becomes: Δx h/λ = h, or Δx=λ. Also in the farfield HUP becomes: λmΔv=h, thus Δv=h/(mλ). Since p=h/λ, then Δv=p/m. Also since p=mc, then Δv=c. So in summary, in the nearfield Δv=infinity, and in the farfield Δv=c, where Δv is the average velocity of the photon according to Pilot Wave theory. Consequently the Pilot wave interpretation should become the preferred interpretation of Quantum Mechanics. It should also be noted that this argument can be applied to all fields, including the graviton. Hence all fields should exhibit instantaneous nearfield and speed c farfield behavior, and this can explain the non-local effects observed in quantum entangled particles.
*YouTube presentation of above arguments: https://www.youtube.com/watch?v=sePdJ7vSQvQ&t=0s
*More extensive paper for the above arguments: William D. Walker and Dag Stranneby, A New Interpretation of Relativity, 2023: http://vixra.org/abs/2309.0145
*Electromagnetic pulse experiment paper showing that an EM pulse propagates in the nearfield with no propagation delay. The paper has just been peer reviewed and accepted for publication in the EM journal IRECAP: https://www.techrxiv.org/doi/full/10.36227/techrxiv.170862178.82175798/v1
Dr. William Walker - PhD in physics from ETH Zurich, 1997
A question, if I may. You say that you object to theories involving action at a distance because they "describe what happens but frame no hypothesis for why". Now, I was under the impression that "describing what happens" - i.e., describing physical phenomena as they in fact occur - was all that any responsible physics ever claimed to do. To be sure, a given phenomenon might turn out to be a particular manifestation of some more basic principle, but that (so I was given to understand) is something you have to find out by investigation, not something you may ever assume a priori. Moreover, if we do come to intuitive assumptions, it seems to me that, all else being equal, the simpler phenomenon ought to be assumed to be more basic than the more complex one. So why should it be any sort of disqualification of a theory that it treats Coulomb's Law as basic, and "the progressive motion of energy from a starting cause to an ending effect" as derived, rather than the other way around?