4.6.2 The Accelerating Charge Model
The Radiation of One Charge Accelerating
What is the sound of one hand clapping? The question is nonsense because applause requires two hands. Then why is our physical conception of radiation centered on the similarly nonsensical concept of one charge accelerating? Read on!
The glow of charged particles moving through rarified gases has long inspired awe and wonder. “It was a most delightful spectacle, when the room was darkened, to see the electricity in its passage,” declared Benjamin Franklin’s friend, William Watson (1715 – 1787) [[i]]. From the darkened salons of the eighteenth century [[ii]], to the “very peculiar and beautiful” observations of electric glow by Michael Faraday (1791–1867) [[iii]], progress in electrical technology, glass blowing, and vacuum pumps, led to William Crookes (1832–1919) and his “cathode ray tubes”
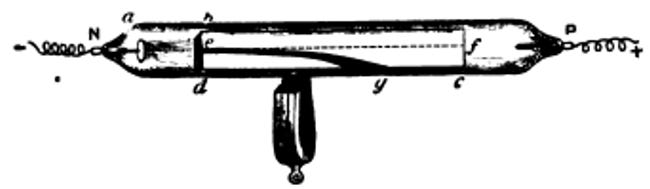
Crookes reported the “radiant matter” emitted from the negative pole, or cathode (a), in one of his tubes, shown in Figure 4.59, would project the length of the tube, illuminating the phosphor screen at f. If a horseshoe magnet were placed underneath the tube, the ghostly ray would bend down under its influence [[iv]]. Crookes was convinced this behavior was due to “molecules” of electricity shot from the cathode.
Joseph John “J.J.” Thomson (1856–1940) was inspired to inquire further. In 1894, J.J. Thompson measured the velocity of cathode rays and found them moving at 2 x 105 meters/second, much slower than the speed of light [[v]]. This result strongly suggested cathode rays were not vibrations in the æther and emboldened the advocates of Crookes’ corpuscular hypothesis. In 1897, Thomson devised an ingenious experiment [[vi]]. By projecting cathode rays through crossed electric and magnetic fields, he was able to determine the charge to mass ratio for Crookes' "molecules" of electricity [[vii]]. We credit Thomson with the discovery of what were soon called electrons.
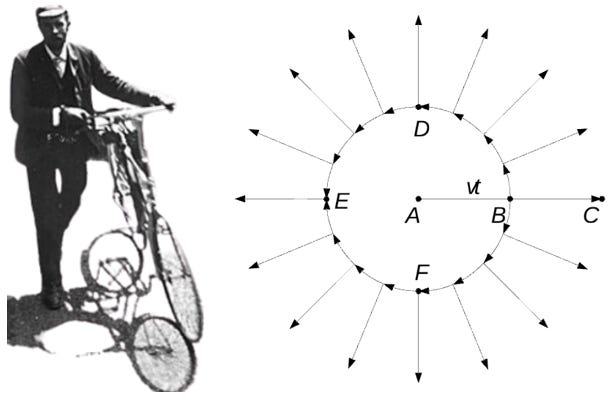
Physicists fixated on the motions of electrons as the source of electromagnetic radiation, the radial fields emanating from these point charges kinked as the influence of an acceleration propagates outward along the radial field lines at the speed of light. Oliver Heaviside presented one of the first diagrams of this behavior in his 1893 text, Electromagnetic Theory [[xi]]. J.J. Thomson's version from 1903 is particularly distinct.
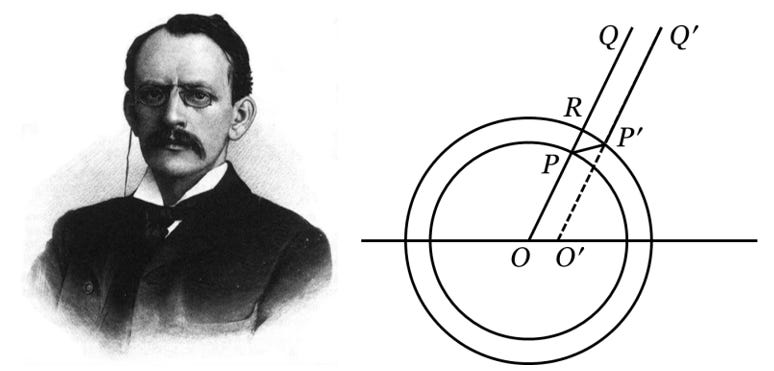
Heaviside derived the equations for radiation from a single accelerating charge in 1902 [[xv]], a result independently rediscovered by the physicist Richard Feynman in the 1950s and presented in his Feynman Lectures on Physics [[xvi]].
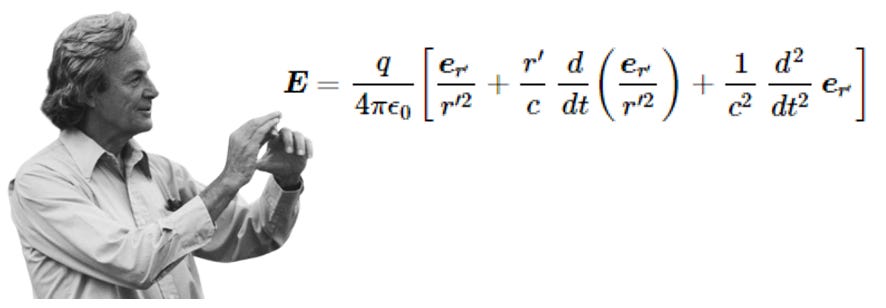
This model of electromagnetic radiation from a single charge is fundamental to contemporary physicists’ thinking about electromagnetism. It is also fundamentally flawed. How so? Sometimes it's helpful to consider a problem from a different perspective.
Zen Buddhism employs stories, dialogues, or questions called “kōans” that are the focus of meditation and through which are the means to acquire insight. One of the greatest teachers of Zen, the Japanese master Hakuin Ekaku (1685–1768) famously instructed his students to “listen to the sound of the single hand” [[xvii]].
What is the sound of one hand clapping?
Applause is a phenomenon that arises from the interaction of two hands. If, obsessed with reductionism, we try to break down applause into a manifestation arising from the behavior of a single hand, we destroy the essential context necessary to give rise to applause.
Now ponder, if you will, the radiation of one charge accelerating. That’s good Zen, perhaps, but it’s very bad physics. How is it possible for an individual isolated charge to accelerate?
Radiation requires – at a minimum – a dipole: equal and opposite charges so overall neutrality is preserved and so the charges can mutually accelerate toward each other.
Why then do we use a formula that assumes a single charge can accelerate? “Shut up and calculate,” they explain. “Just assume it does.” We have a formula that describes radiation from a charge as a function of acceleration, and pretty pictures of kinked field lines to justify it.
The physicists’ theory sort of works, except for the part where Gauss’ Law requires that electromagnetic radiation comprises closed field lines. Whatever the validity of the kinked field-line model, the field lines don’t close, and this “model for radiation” isn’t.
Further, an accelerating charge, in the physicists’ picture, presents a moving violation of the law of conservation of energy. Somehow contained in that infinitesimal charge is an infinite amount of energy, because if we keep accelerating it, the charge keeps on pumping out the radiation energy. “Don’t be silly,” a physicist would counter. “It takes work to make the charge accelerate and the energy comes from there.” Precisely my point. However, that mysterious agent of work is nowhere in the conventional theory, and physicists just assume that somehow the energy miraculously appears at the location of the charge to be radiated away.
Why is that a problem? There’s another minor issue in the conventional wisdom: the part where the moment a charge accelerates, the radiation exerts a reaction force on the charge that causes more acceleration. And thus, more radiation. Which makes even more acceleration. And necessarily, still more radiation. So, we end up with a theory in which the slightest acceleration leads to an exponential runaway in both radiation and acceleration. Other than that minor problem – the problem of “radiation reaction” –conventional theory works well.
I have a different theory to offer you. In my theory, accelerating charges don't radiate – they absorb energy. As they accelerate, their kinetic energy increases. An accelerating charge is a tiny current and the faster it goes, the more magnetic energy it collects in its vicinity. Whether one looks at it electromagnetically or looks at it mechanically, an accelerating charge absorbs energy.
The field doing the acceleration supplies the radiated energy, and in many cases the source of radiation energy is nowhere near the accelerating charge. My theory is consistent with Gauss’ Law, it conserves energy, and it works. The conventional wisdom simply doesn’t. We will pick up the topic of radiation in Chapter 8.
“Hold it right there,” physicists will say. “Extraordinary claims require extraordinary evidence. You can't just overthrow a century of physical understanding. You have to present an ‘experimentum crucis,’ some experimental test to prove that your theory works better than the theory we've all accepted for over a century.”
Challenge accepted. I’ll offer you an experimentum crucis.
In fact, YOU can perform the experiment yourself, right now. Sit very, very still. Now, move your hand until it contacts the nearest solid object. The moment you started accelerating your hand, did the electrons and protons of the matter comprising your hand accelerate madly up to the speed of light, destroy you in a burst of energy, and set off a shock wave that accelerates all the matter of the Earth until it's moving outward infinitesimally close to the speed of light and all that is left is a supernova of energy radiating outward where our planet used to be?
That didn't happen? Good. That’s what my theory predicts.
Fields & Energy is not only about “how electromagnetism and quantum mechanics work,” but also about “where physics went wrong.” How is it that physicists could have become stuck on a problematic electromagnetic theory, unable to update and correct it for over a century? We’ve already seen in the author’s introduction how the top graduate-level physics textbook presents an atrophied version of 1940s-era applied electromagnetism, leaving today’s physicists less well informed about applied electromagnetic physics than their predecessors of eighty years ago. Some will argue that intelligence and per capita levels of genius peaked in the nineteenth century, and that's why progress has stalled since the days of Maxwell, Heaviside, and Hertz [[xviii]]. All these factors may play a role. The critical transition period, however, is coming up in Chapter 5, as physicists went careening into the realm of quantum mechanics while under the influence of some stunningly bad philosophic preconceptions.
Next time: 4.7 Summary & Conclusions
Enjoyed the article, but maybe not quite enough to spring for a paid subscription?
Then click on the button below to buy me a coffee. Thanks!
Full Table of Contents [click here]
Chapter 4 Electromagnetism Comes of Age
4.6.2 The Accelerating Charge Model
4.7 Summary & Conclusions
Follow Online:
You may follow me online in other places as well:
Telegram: 𝔸𝕖𝕥𝕙𝕖𝕣𝕔𝕫𝕒𝕣'𝕤 𝔸𝕖𝕥𝕙𝕖𝕣𝕤𝕥𝕣𝕖𝕒𝕞
Gab: @aetherczar
Twitter: @aetherczar
Amazon: Hans G. Schantz
References
[[i]] Pais, Abraham, Inward Bound: Of Matter and Forces in the Physical World, Oxford: Clarendon Press, 1986, pp. 78-79. See: https://amzn.to/4dVtdWh
[[ii]] Bertucci, Paola, “Sparks in the dark: the attraction of electricity in the eighteenth century,” Endeavor, Vol. 31, No. 3, 6 August 2007, pp. 88-93. See: https://hshm.yale.edu/sites/default/files/files/Bertucci%20Endeavour.pdf
[[iii]] Faraday, Michael, Experimental Researches, London: Richard and Edward Taylor, 1839, §1526-1543, pp. 486-490. Reprinted from the Philosophic Transactions of 1831-1838.
[[iv]] W. Crookes, “On Radiant Matter,” Popular Science Monthly, vol. 16, 1879, pp. 157-167. See also part one at pp. 13-24.
[[v]] Thomson, J.J., “On the Velocity of the Cathode Rays,” Philosophical Magazine, vol. 38, 1894, pp. 358-365.
[[vi]] Pais, Abraham, Inward Bound: Of Matter and Forces in the Physical World, Oxford: Clarendon Press, 1986, pp. 85-86. See: https://amzn.to/4dVtdWh
[[vii]] Thomson, J.J., “Cathode Rays,” Philosophical Magazine, vol. 44, no. 269, October 1897, pp. 293-316. See: https://www.google.com/books/edition/Philosophical_Magazine/utXnmtFZ6TUC?hl=en&gbpv=1&bsq=thomson
[[viii]] Crookes, Op. Cit. Fig. 14, p. 160.
[[ix]] Public domain photo of Heaviside ~1890s. Courtesy IET Archive. See:
https://twitter.com/IETLibArch/status/1135463701081989120
[[x]] Heaviside, Oliver, Electromagnetic Theory, Vol. 1, London: “The Electrician” Printing and Publishing Company, Limited, 1893, p. 55.
[[xi]] Heaviside, Oliver, Electromagnetic Theory, Vol. 1, London: “The Electrician” Printing and Publishing Company, Limited, 1893, p. 55.
[[xii]] https://infogalactic.com/info/File:J.J_Thomson.jpg
[[xiii]] Thomson, J.J., Electricity and Matter, New York: Scribner & Sons, 1908, p. 56.
[[xiv]] Feynman at the Robert Treat Paine Estate in Waltham, Massachusetts, in 1984. Photo of Richard Feynman, taken in 1984 in the woods of the Robert Treat Paine Estate in Waltham, MA, while he and the photographer worked at Thinking Machines Corporation on the design of the Connection Machine CM-1/CM-2 supercomputer. Copyright Tamiko Thiel 1984 - communication from photographer CC BY-SA 3.0 https://en.wikipedia.org/wiki/Richard_Feynman#/media/File:RichardFeynman-PaineMansionWoods1984_copyrightTamikoThiel_bw.jpg
[[xv]] Heaviside, Oliver, “The Waste of Energy from a Moving Electron,” Nature, vol. 67, November 6, 1902, pp. 6-8. See: https://archive.org/details/sim_nature-uk_1902-11-06_67_1723/page/6/mode/2up
[[xvi]] Feynman, Richard P., Robert B. Leighton, Matthew Sands, The Feynman Lectures on Physics, vol. 1, Reading Massachusetts: Addison-Wesley Publishing Company, 1963, p. 28-2. Also, vol. 2, p. 21-1. See: https://www.feynmanlectures.caltech.edu/I_28.html and https://www.feynmanlectures.caltech.edu/II_21.html.
[[xvii]] Seo, Audrey Yoshiko, The sound of one hand : paintings and calligraphy by Zen master Hakuin, Boston: Shambala, 2010, p. 7.
[[xviii]] Dutton, Edward, and Michael Woodley of Menie, At Our Wits End: Why We’re Becoming Less Intelligent and What It Means for the Future, Exeter: Imprint Academic, 2018.






I don't want to do the experiment where I turn into a supernova, if that's OK with you? Just want to be clear about that before we get to Chapter 8.
"Consider a spherical cow" is apparently a warning, as much as it is a joke.
So many simplified of models may be geared to get as rapidly as possible to the calculation phase. But, we have to ask the question "can the model be linked directly back to the actual physical phenomenon under consideration, or via a more complex model of similar type and kind?"
How many of these models are Taylor Series expansions that are "epicycled" into a calculation mode, then set aside as good enough to grind out the necessary numbers?
Grief, now I am thumbing through old textbooks.